Eine knappe Erklärung von der Kosinus-Formel des Skalarprodukts

Das Skalarprodukt (auf Englisch: dot product) ist eine elementare mathematische Verknüpfung, die einem Paar von Vektoren eine Skalarzahl zuordnet. Ich glaube, ich habe davon zum ersten Mal ausdrücklich erfahren, als ich den Kurs namens "Calculus 3" in meiner Uni belegte. Es ist sehr einfach zu rechnen: das Skalarprodukt ist die Summe der Produkte der beziehungsweisen Koordinaten der Vektoren.

$$\mathbf{x}\cdot\mathbf{y} = x_1 y_1 + x_2 y_2 + \cdots + x_n y_n$$

Es ist doch häufig eingesetzt, um den Wert des Winkels $\vartheta$ zu kalkulieren, der zwischen den Vektoren eingeschlossen ist, denn es gilt auch, dass:

$$\mathbf{x}\cdot\mathbf{y} = \lVert \mathbf{x}\rVert \cdot\lVert \mathbf{y}\rVert \cdot \cos\vartheta$$

Dies ist eine sehr wichtige Formel, die überall bei der multivariaten Analyse, linearen Algebra, Geometrie usw. eingesetzt wird. Doch wie beweist man eigentlich diese Kosinus-Formel, wenn man nur die erste Formel für die Definition des Skalarprodukts annimmt? Es gilt als elementar, aber ist gar nicht offensichtlich. Trotzdem hat mir kein einziges Mal ein Professor oder Lehrbuch die Verbindung zwischen diese zwei Formeln ausdrücklich erläutert.

Dazu wollte ich einen sehr knappen Gedankengang darstellen, der es ermöglicht, diese Kosinus-Formel "auf einen Blick" zu erfassen. Es ist nichts Besonderes, aber ich habe so was eigentlich nie eindeutig niedergeschrieben.

Man kann die Kosinus-Formel für das Skalarprodukt einfach beweisen, wenn man bereit ist, die folgenden "offensichtliche" (oder mindestens intuitivere) Tatsachen anzunehmen:

• die Drehungen in $\mathbb R^n$ behalten die Winkel zwischen Vektoren
• die Drehungen in $\mathbb R^n$ behalten Distanzen zwischen Paaren von Punkten
• für jedes Paar von Vektoren $\mathbf{x},\mathbf{y}\in\mathbb R^n$ gibt es eine Drehung um den Ursprung, die sie in die XY-Ebene bringen

Dieser Gedankengang beruht sich hauptsächlich auf der grundsätzlichen algebraischen Tatsache $(x-y)^2 = x^2 - 2xy + y^2$. Anders gesagt lautet diese Gleichung:

$$x\cdot y = \frac{x^2 + y^2 - (x-y)^2}{2}$$

Seien $\mathbf{x},\mathbf{y}\in\mathbb R^n$ zufällige Vektoren, wenn man diese Gleichung komponentenweise auf diese zwei Vektoren anwendet, dann bekommt man die Gleichung

$$\mathbf{x}\cdot\mathbf{y} = \frac{\lVert \mathbf{x}\rVert^2 + \lVert\mathbf{y} \rVert^2 - \lVert \mathbf{x} - \mathbf{y} \rVert^2}{2}$$

Das heißt, dass $\mathbf{x}\cdot\mathbf{y}$ nur von den drei Distanzen $\lVert \mathbf{x}\rVert, \lVert\mathbf{y} \rVert, \lVert \mathbf{x} - \mathbf{y} \rVert$ abhängt. Laut unserer Voraussetzungen muss jede Drehung die Distanzen zwischen Punkten behalten. Sei dann $U$ eine Drehung um den Ursprung, denn behaltet es die Werte der Ausdrücke $\lVert \mathbf{x}\rVert, \lVert\mathbf{y} \rVert, \lVert \mathbf{x} - \mathbf{y} \rVert$. Daraus folgt, dass

$$\mathbf{x}\cdot\mathbf{y} = U\mathbf{x}\cdot U\mathbf{y}$$

Unsere dritte Voraussetzung lautet, dass es eine bestimmte Drehung $U$ gibt, die $\mathbf{x},\mathbf{y}$ gleichzeitig in der XY-Ebene bringt. Also haben wir gefolgert, dass es jedem Paar von Vektoren $\mathbf{x}, \mathbf{y}$ ein anderes Paar von Vektoren $\mathbf{x}' = U\mathbf{x}, \mathbf{y}' = U\mathbf{y}$ in der XY-Ebene entspricht, das sowohl das gleiche Skalarprodukt als den gleiche Winkelwert hat. Das heißt: die Formel gilt im Allgemeinen, solange es im zweidimensionalen Fall gilt, wobei $\mathbf{x} = (x_1,x_2)$ und $\mathbf{y} = (y_1,y_2)$.

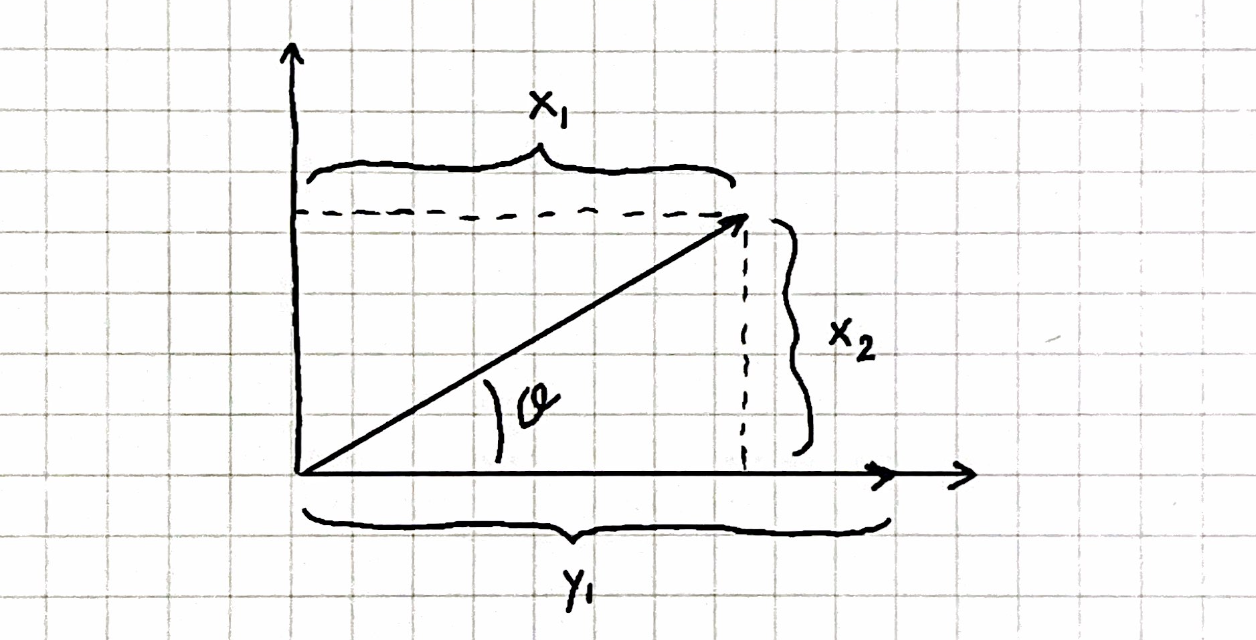
Im zweidimensionalen Fall ist die Formel doch sehr einfach zu beweisen. Durch einer weiteren Drehung um den Ursprung kann man $\mathbf{y}$ parallel zu der X-Achse richten, damit $\mathbf{x} = (x_1,x_2)$ und $\mathbf{y} = (y_1, 0)$. In diesem allereinfachsten Fall reduziert sich die KosinusFormel auf $$x_1 y_1 = \sqrt{x_1^2 + x_2^2}\cdot y_1 \cos\vartheta$$ oder $$\frac{x_1}{\sqrt{x_1^2 + x_2^2}} = \cos\vartheta$$ Diese Gleichung ist doch bloße zweidimensionale Trigonometrie:

Und das war's!

Übrigens frage ich mich, ob man irgendeine Verbindung zwischen dem Skalarprodukt und der Galoistheorie von Rationalfunktionkörper erweisen kann. Der Kern unseres früheren Beweis war die Tatsache, dass die Drehungen um den Ursprung behalten das Skalarprodukt, also, das Polynom $x_1 y_1 + \cdots + x_n y_n$. Deshalb frage ich mich zum Beispiel, ob der Unterkörper von $\mathbb R(x_1,\cdots, x_n, y_1,\cdots, y_n)$, die aus den von gleichzeitigen linearen Drehungen behaltenen rationalen Funktionen besteht, genau $\mathbb R(\lVert \mathbf{x}\rVert^2, \lVert \mathbf{y}\rVert^2, \mathbf{x}\cdot\mathbf{y})$ ist. Das habe ich doch bis jetzt weder bestätigt noch widerlegt.