Untersuchung von einer schwingenden Beatty-artigen Folge

Die Beatty-Folgen sind ein weniger bekanntes Thema der Mathematik, das mich besonders interessiert. Dazu habe ich letztens die folgende schwankende Folge von Summen untersucht, die die Verteilung von geraden und ungeraden Zahlen in der Beatty-Folge des Goldenen Schnitts enthält:

$$s(n) = \sum_{k=1}^n (-1)^{\lfloor \phi k\rfloor}$$

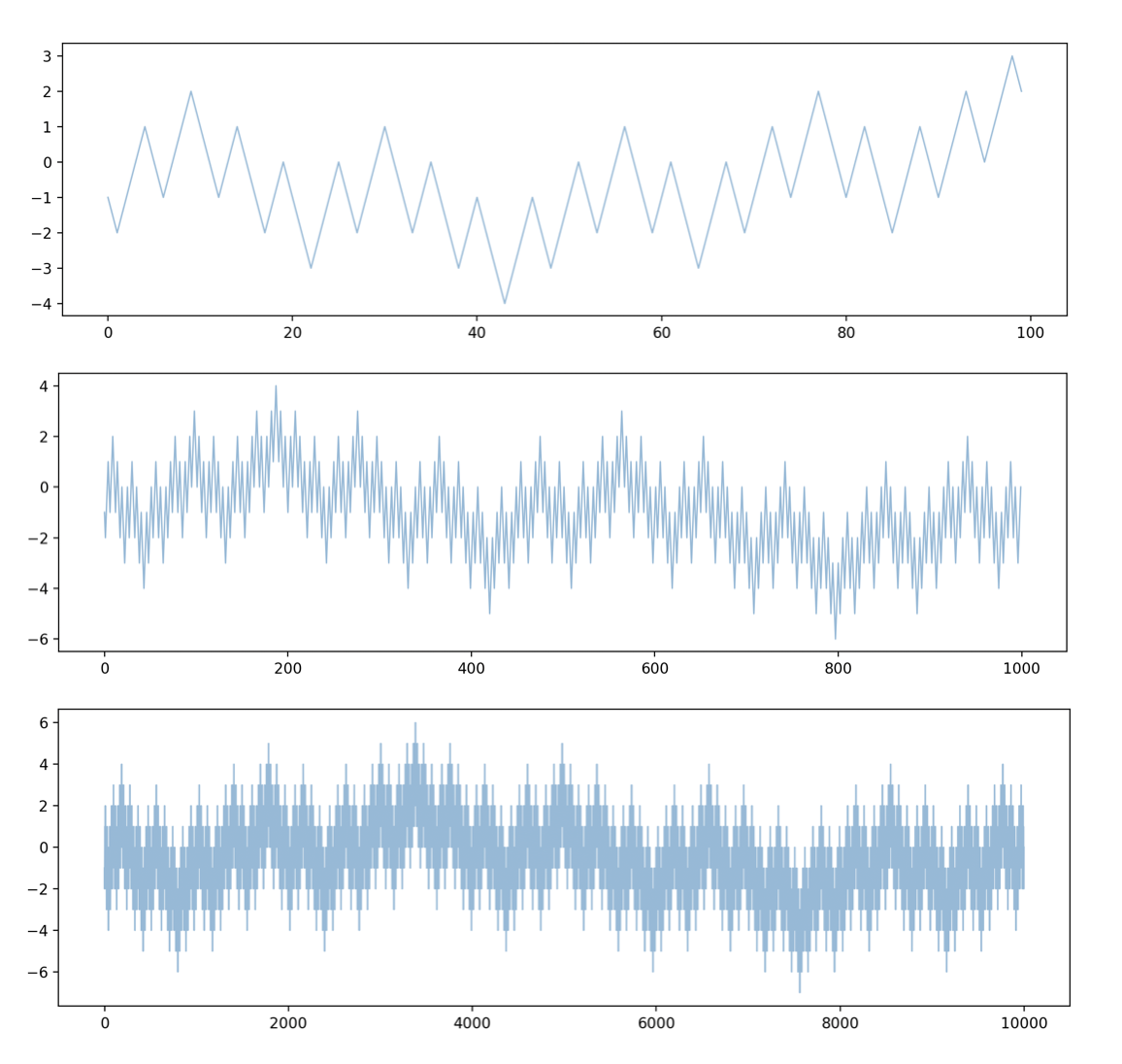
Diese Folge sieht so aus:

Wegen der Irrationalität von $\phi$ sehen die Höhen und Tiefen dieser Folge zwar ein wenig wie die einer Zufallsbewegung aus. In den Graphen tritt auch eine gewisse Selbstähnlichkeit auf. Ich habe sehr befriedigende Antworten zu den folgenden Fragen bezüglich $s(n)$ entdeckt, und ich würde den Lesern auch vorschlagen, mal zu versuchen, sie zu lösen:

• Sind die Werte von $s(n)$ begrenzt?
• Wenn ja, was ist eine obere Grenze für $|s(n)|$?
• Wenn nein, mit welcher Wachstumsklasse wachsen die Höchstwerte und Minderwerte von $s(n)$?
• Wie kann man die Werte von $s(n)$ effizient kalkulieren?

Mithilfe einiger günstigen Sätzen betreffend die Kettenbrüche lässt sich eine sehr nützliche rekursive Formel für $s(n)$ beweisen, die die Lösung dieser Fragen sehr viel vereinfacht.

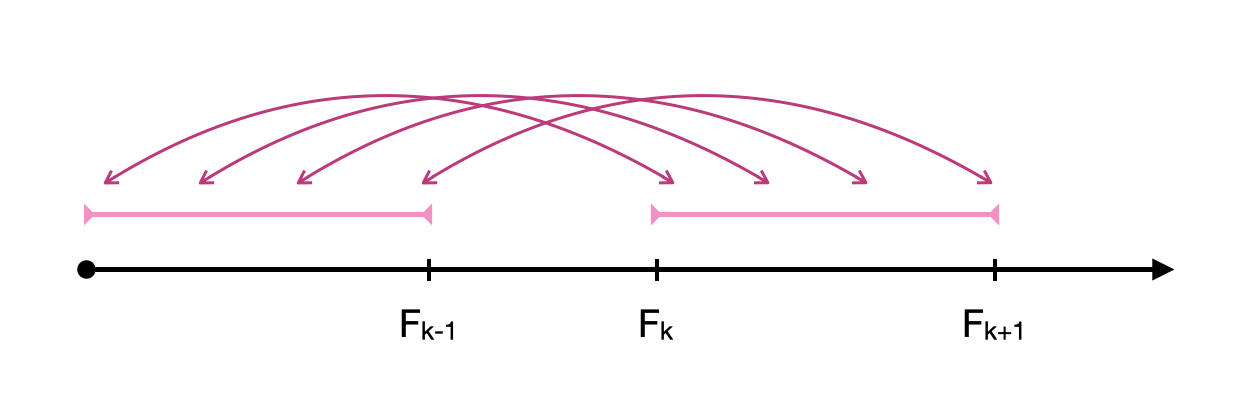
Für die Konvergenten $p/q$ eines Kettenbruchs, der der irrationalen Zahl $\alpha$ entspricht, gilt: $$\bigg|\alpha - \frac{p}{q}\bigg| \leq \frac{1}{q^2}$$ und umgekehrt, wenn eine rationale Zahl $p/q$ näher als $1/2q^2$ zu $\alpha$ ist, muss es eine Konvergente des Kettenbruchs von $\alpha$ sein. Die Fibonacci-Zahlen sind die besondere Konvergenten der rationalen Zahl $\phi$, deshalb: seien $n,k\in\mathbb N$ sodass $n < F_{k-1}$ und sei $N$ die nächste natürliche Zahl zu $\phi n$, so gilt $$|\phi n - N| \geq n\cdot \bigg|\phi - \frac{N}{n}\bigg|\geq \frac{1}{2n} > \frac{1}{2F_{k-1}}$$ und andrerseits $$|\phi F_k - F_{k+1}| = F_k\cdot \bigg|\phi - \frac{F_{k+1}}{F_k}\bigg|\leq \frac{1}{F_{k+1}} \leq \frac{1}{2F_{k-1}}$$

denn es gilt, dass $F_{k+1} \geq 2F_{k-1}$ für jede $k \geq 1$. Das heißt, die Größe $|\phi F_k - F_{k+1}|$ ist kleiner als die Distanz zwischen $\phi n$ und der nächsten ganzen Zahl, damit $\phi n$ und $\phi n +(\phi F_k - F_{k+1})$ der gleichen Abrundung entsprechen müssen: $$\lfloor \phi n \rfloor = \lfloor \phi n + (\phi F_k - F_{k+1})\rfloor$$ und deshalb: $$\lfloor \phi (n + F_k)\rfloor = \lfloor \phi n\rfloor + F_{k+1}$$ Tatsächlich gilt diese Formel auch wann $n=F_{k-1}$, nicht nur $n < F_{k-1}$. Diese Identität ergibt eine rekursive Formel, die beim Kaltulieren größerer Werte der Funktion $s(n)$ sehr behilflich ist: $$\begin{align*} s(F_{k}+n) &= \sum_{j=1}^{F_{k}+n} (-1)^{\lfloor \phi j\rfloor} \\ &= \sum_{j=1}^{F_k} (-1)^{\lfloor \phi j\rfloor} + \sum_{j=F_k+1}^{F_k+n} (-1)^{\lfloor \phi j\rfloor} \\ &= \sum_{j=1}^{F_k} (-1)^{\lfloor \phi j\rfloor} + \sum_{j=1}^{n} (-1)^{\lfloor \phi (j+F_k)\rfloor} \\ &= \sum_{j=1}^{F_k} (-1)^{\lfloor \phi j\rfloor} + \sum_{j=1}^{n} (-1)^{\lfloor \phi j\rfloor + F_{k+1}} \\ &= s(F_k) + (-1)^{F_{k+1}}s(n) \end{align*}$$ Die Folge von Restklassen modulo $2$ der Fibonacci-Zahlen ist periodisch modulo $3$, damit jede dritte Fibonacci-Zahl gerade ist. Deshalb können wir die Formel auf diese Weise simplifizieren: $$s(F_k + n) = s(F_k) + (-1)^{[\![ k \not\equiv 2 \bmod 3 ]\!]}s(n)$$

Mit Hilfe von dieser Rekursionsgleichung ist es ganz einfach zu beweisen, dass die Teilfolge $s(F_k)$ deshalb auch periodisch ist. Offensichtlich ist $s(F_{k+1})$ nur auf $s(F_k)$, $s(F_{k-1})$ und $k\bmod 3$ abhängig und durch manuellen Rechnung kann man einfach bestätigen, dass $s(F_1) = s(F_7)$ und $s(F_2) = s(F_8)$ und davon folgern, dass $s(F_k) = s(F_{k+6})$ für alle $k\in\mathbb N$:

$$\begin{array}{l|l|l|l} n & F_n & (-1)^{F_n} & s(F_n) \\\hline 1 & 1 & -1 & -1 \\ 2 & 1 & -1 & -1 \\ 3 & 2 & 1 & -2 \\ 4 & 3 & -1 & -1 \\ 5 & 5 & -1 & 1 \\ 6 & 8 & 1 & 0 \\ 7 & 13 & -1 & -1 \\ 8 & 21 & -1 & -1 \\ 9 & 34 & 1 & -2 \\ 10 & 55 & -1 & -1 \\ 11 & 89 & -1 & 1 \\ 12 & 144 & 1 & 0 \\ \vdots & \vdots & \vdots & \vdots \\ \end{array}$$

Diese Periodizität trivialisiert die Rechnung des Glieds $s(F_k)$ in der rekursiven Formel und deshalb ergibt sie im Grunde eine Beziehung zwischen den Werten von $s(n)$ im Bereich $[F_k,F_{k+1}]$ und den Werten von $s(n)$ im Bereich $[1, F_{k-1}]$.

Der Satz von Zeckendorf besagt, dass jede natürliche Zahl in eine Summe von Fibonacci-Zahlen aufgelöst werden kann, derart, wobei keine zwei aufeinanderfolgenden Fibonacci-Zahlen in der Summe vorkommen. Die natürliche Zahlen lassen sich algorithmisch sehr effizient in ihre Zeckendorfzerlegungen auflösen. Deshalb ermöglicht die rekursive Formel für $s(n)$ die Rechnung von exakten Werten von $s(n)$ auch wenn $n$ so groß ist, dass es gar nicht praktisch wäre, $s(n)$ als eine Summe von $n$ Termen zu berechnen. Zum Beispiel, ich habe ein kleines Haskell-Programm geschrieben, die unsere Formel benutzt, um die folgende Werte von $s(n)$ zu rechnen:

$$\begin{array}{l|l} n & s(F_n) \\\hline 10^{10} & 0 \\ 10^{50} & 2 \\ 10^{100} & -12 \\ 10^{500} & -4 \\ 10^{1000} & 30 \\ 10^{5000} & 10 \\ 10^{10000} & 72 \\ \end{array}$$

Mithilfe der rekursiven Formel ist es auch ziemlich einfach zu beweisen, dass die folgende Formeln für sonderliche Werten der Folge $s(n)$ gelten:

$$\begin{align*} & s(F_3 + F_6 + \cdots + F_{6n+3}) = -2n \\ & s(F_3 + F_6 + \cdots + F_{6n+3} + F_{6n+4}) = 2n-1 \\ & s(F_3 + F_6 + \cdots + F_{6n+6}) = 2n \\ & s(F_3 + F_6 + \cdots + F_{6n+6} + F_{6n+8}) = -(2n+1) \\ \end{align*}$$

was bestätigt, dass $s(n)$ weder nach oben noch nach unten beschränkt ist. (Ich glaube, dass diese Eingabewerte für $s$ sind genau jene, wo es seine Höchstwerte und Mindestwerte zum ersten Mal annimmt, aber es ist mir noch nicht gelungen, das zu beweisen.) Wir können folgern, dass die Höchstwerte von $s(n)$ logarithmisch wachsen, denn die Fibonacci-Zahlen exponentiell wachsen: $$\sup_{1\leq k\leq n} s(k) = \mathcal O(\log n)$$

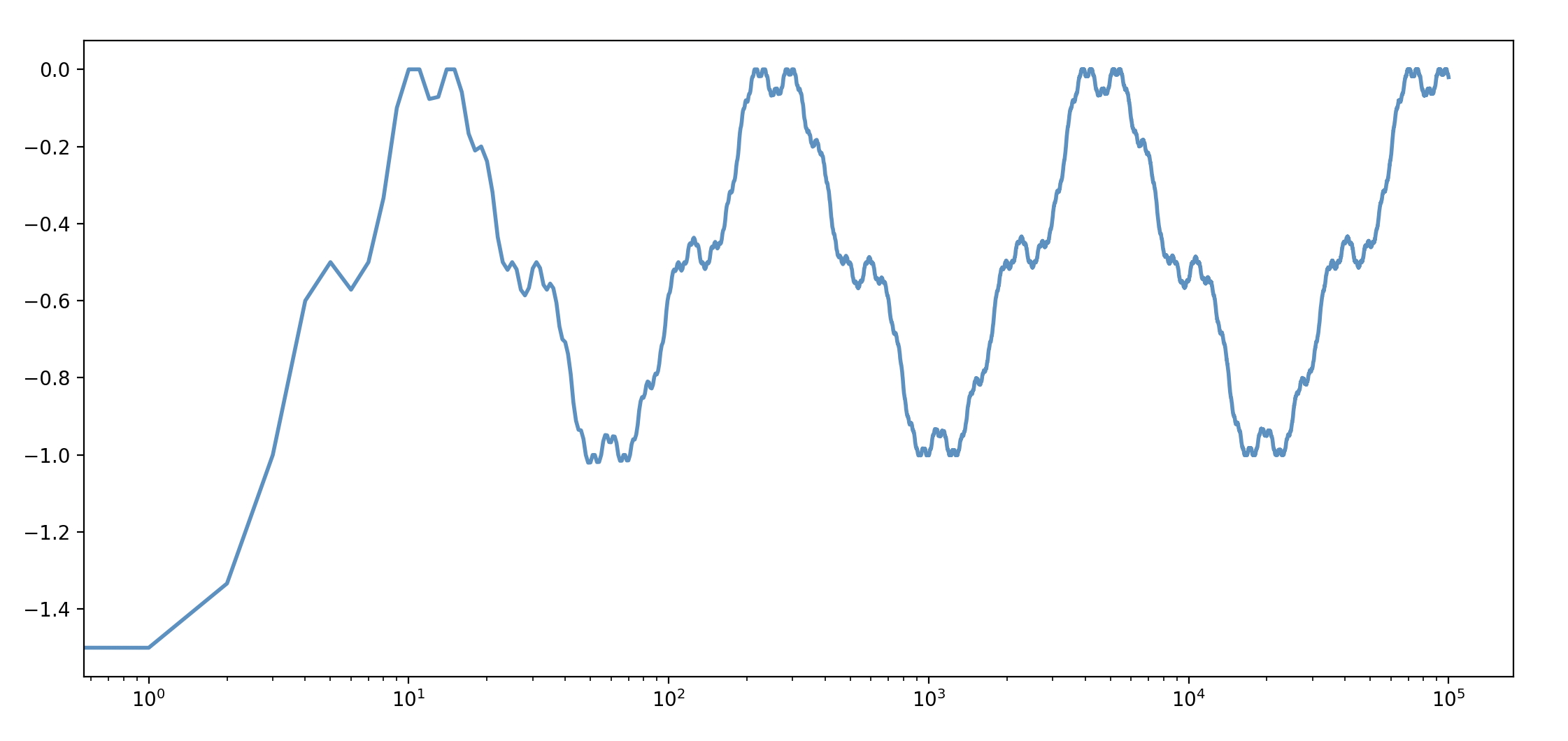
Zum Schluss möchte ich diesen Blogeintrag mit ein paar weiteren Fragen abschließen. Erstens: kannst du diese Technik erweitern, um die Rechnung von Summen wie z.B. $$\sum_{k=1}^n \omega^{\lfloor \alpha k\rfloor}$$ zu ermöglichen, wobei $\omega$ eine komplexe Einheitswurzel ist und $\alpha\notin \mathbb Q$? Zweitens: offensichtlich ergibt $s(n)$ eine divergierende Reihe als $n\to\infty$, aber kannst du beweisen, ob oder nicht diese Reihe sich durch einer anderen Summierungsweise wie z.B. Cesàro-Summierung einen Wert zuzuschreiben läßt? Der folgende Graph, der die Cesaro-Partialsummen von $s(n)$ halblogarithmisch darstellt, deutet überzeugend an, dass diese Summen auch so divergieren: