Skip to page content Home     Posts     CV     Contact     People

The Lemniscate

2016 Dec 27

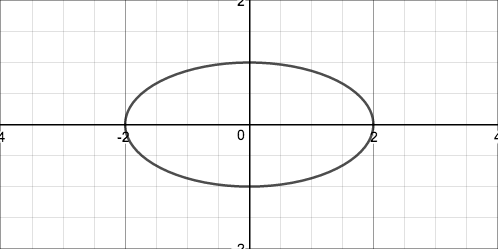
After creating a tilted parabola, I started looking into other types of graphs that are also loci of points. A locus is a set of all points fulfilling some specific condition, like the parabola, the locus of all points equidistant from the focus point and the directrix line. One simple locus is a circle, which is the locus of all points some given distance from another point, the center of the circle. Another example is the ellipse, which is the locus of all points the sum of whose distances from two foci is equal to a constant. Here is an example of what an ellipse might look like:

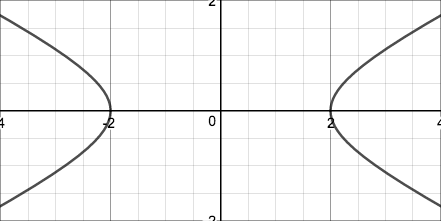
Another type of locus is the hyperbola, which is the locus of all points the difference of whose distances from each of two foci is equal to a constant. Here is a hyperbola:

After studying the ellipse and hyperbola for a only a short time, I began to get bored, because almost everything that there was to know about the ellipse and hyperbola was already discovered. So I decided to make my own locus, which was the locus of all points the product of whose distances from each of two foci was equal to a constant. I decided to let the foci be the points $(x_0,0)$ and $(-x_0,0)$ (so that it would be symmetric about the y-axis) and let this be equation of the locus:

$$\sqrt{y^2+(x-x_0)^2}*\sqrt{y^2+(x-x_0)^2}=c$$

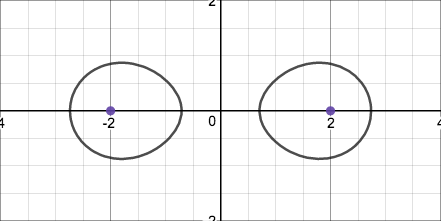
As I played around with this graph, I found that it makes three basic types of shapes. The first consists of two disjoint closed curves that are vaguely egg-shaped,

the second consists of two pointed closed curves sharing a single point,

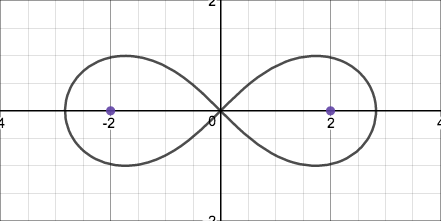
and the third consists of a single closed curve that is pinched in the middle.

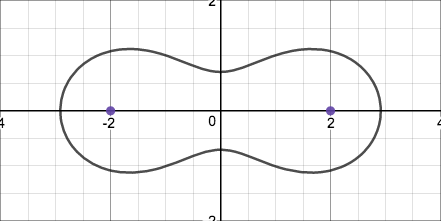
In order to determine when it takes each of these shaped, I decided to define the line equidistant from each of the lemniscate's foci as the axis of the lemniscate. I could then classify each shape by the number of times it intersected its axis: the first shape does not intersect its axis, the second intersects it at $1$ point, and the third intersects it at $2$ points. I could then determine algebraically when each shape would occur by setting $x$ to $0$ (because when the lemniscate is symmetric about the y-axis, the points at which it intersects its axis are at $x=0$). Then I could obtain a simpler expression by solving for the y-position at which the lemniscate would intersect its axis:

$$\sqrt{y^2+(-x_0)^2}*\sqrt{y^2+{x_0}^2}=c$$ $$\sqrt{y^2+{x_0}^2}*\sqrt{y^2+{x_0}^2}=c$$ $$y^2+{x_0}^2=c$$ $$y^2=c-{x_0}^2$$

Now, in order to generalize my findings for any lemnicate not necessarily lying on the x-axis or symmetric about the y-axis, I decided to let $d$ be the distance between the foci so that $d=2x_0$ and ${x_0}^2=\frac{1}{4}d^2$, and I replaced $$y^2=c-{x_0}^2$$ with $$y^2=c-\frac{1}{4}d^2$$ Then I could easily determine when each of the shapes would be made because

1. When $c<\frac{1}{4}d^2$, $c-\frac{1}{4}d^2$ would be a negative number. This means that $y^2$ would have to be equal to a negative number, and there would be no real intersections between the lemniscate and its axis.

2. When $c=\frac{1}{4}d^2$, $c-\frac{1}{4}d^2$ would be zero. This means that $y^2$ would have to be equal to 0, and there would be exactly one intersection (i.e. at $y=0$).

3. When $c>\frac{1}{4}d^2$, $c-\frac{1}{4}d^2$ would be a positive number. This means that $y^2$ would have to be equal to a positive number, and there would be exactly two intersections with ordinates $y=+\sqrt{c-\frac{1}{4}d^2}$ and $y=-\sqrt{c-\frac{1}{4}d^2}$.

That's all I'm doing with the lemniscate for now, but it is a very interesting subject and I will surely return to it later.