Skip to page content Home     Posts     CV     Contact     People

Sudoku en C

Este semestre asisto CS241, una clase de algoritmos y estructuras de datos en UNM. Como nuestro primer gran proyecto tuvimos que construir un algoritmo en C (el lenguaje que usaremos durante toda la clase) que resuelve las rompecabezas de Sudoku. Dado una cuadrícula parcialmente completada, debe o devolver una solución posible o concluir que el rompecabezas no sea posible. Como pasé un par de días jugando con esta tarea y me ha resultado muy divertida (por lo menos mucho más que solucionar los Sudoku a mano), en esta entrada me pongo a describir mi algoritmo, algunas optimizaciones, y además los resultados de unos experimentos numéricos que he llevado a cabo con el código.

La estructura del algoritmo

Para dar un repaso: un Sudoku es un rompecabezas que consiste en una cuadrícula de nueva filas y nueve columnas, en la cual la mayoría de las entradas quedan en blanco, pero algunos contienen un número de $1$ a $9$. En un Sudoku correctamente resuelto, cada entrada contiene un número de tal manera que cada cifra aparece exactamente una vez en cada una de las nueve filas, columnas, y $3\times 3$ minicuadrículas; es decir que el rompecabezas rellenado constituye un cuadrado latino. Si quieres probar suerte con Sudoku, puedes practicar aquí todo lo que quieras.

Al jugar, te darás cuenta muy pronto que resolver Sudoku es un trabajo bastante repetitivo. Lo primero que hago yo es buscar entradas vacías cuyas valores quedan determinados por las otras entradas llenas en la misma fila, columna o minicuadrícula. En concreto, si la fila, columna y minicuadrícula de una entrada ya contienen juntos cada cifra salvo una, sabemos que ésta debe ser nuestro número desconocido, suponiendo que nuestro Sudoku aún tiene solución. Llenar esta entrada nos da la oportunidad de adivinar los valores de aún otras usando esta información nueva, etcétera. Sin embargo, esta estrategia no necesariamente basta para resolver un Sudoku, es decir, es posible encontrarse en el apuro de no poder deducir el valor de ni una entrada más de esta manera, aunque el rompecabezas posea una solución única.

En este caso hay que hacer una conjetura sobre el valor de una de las entradas todavía no determinadas y correr el peligro de perder tiempo en un ramal equivocado del sendero de soluciones que bifurca. Si llenas una entrada con una suposición aleatoria y las deducciones que siguen te llevan a una situación imposible, hay que volver atrás, eliminar esta posibilidad, y suponer otro. Pero es posible que tendrás que hacer dos, tres o aún más suposiciones antes de llegar a una calle ciega, y quedarse dentro de varios hipotéticos anidados. Recuerda a un algoritmo recurrente, ¿no?

En mi código he escrito funciones especializadas para cumplir cada parte de ese proceso:

• boardStatus(int board[9][9]) determina si una cuadrícula queda en un estado solucionado, no solucionado, o imposible (que indica que no tiene solución ninguna).
• eliminateEntries(int board[9][9], int i, int j) mira a la entrada en la posición i, j y si queda ya determinado, elimina su valor de la lista de posibilidades de cada otra entrada en la misma fila, columna, o minicuadrícula.
• eliminateAllEntries(int board[9][9]) aplica eliminateEntries a cada entrada de la cuadrícula, así llevando a cabo cada deducción posible (de primer órden).
• makeGuess(int board[9][9]) y sudokuSolver(int board[9][9]) son un par de funciones recurrentes que se llaman la una a la otra.
  • makeGuess(int board[9][9]) acepta como argumento una cuadrícula no solucionado y busca una entrada todavía no determinada para probar cada valor posible y llamar a sudokuSolver para determinar la validez de cada suposición, hasta o encontrar una solution o agotar todas las posibilidades y concluir que no haya solución.
  • sudokuSolver(int board[9][9]) aplica eliminateAllEntries a la cuadrícula varias veces, y si todavía no queda solucionado ni en un estado imposible, llama a makeGuess para empezar a adivinar los valores de las entradas.

Sólo unas pocas palabras más sobre el diseño de la cuadrícula en mi código. Uso un int[9][9] para cifrar una cuadrícula parcialmente o totalmente solucionada, pero las entradas no son números entre $1$ y $9$, sino entre $0$ y $511$, para que puedan representar no sólo entradas ya determinadas, sino también las entradas sobre cuyas valores tenemos algúna información aunque todavía hay incertidumbre. Cada número entero entre $0$ y $511$ tiene una representación binaria de $9$ figuras, por ejemplo $510 = 111111110_2$. El enésimo bit de una entrada indica si es posible que esa entrada tome el valor $n$. Por ejemplo, si supiéramos con certeza que una entrada contuviera un $4$, la llenaríamos con el número

$$000001000_2 = 8$$

Por otro lado, si pudiéramos descartar las posibilidades $1,2,4$ y $8$ para una entrada sin saber su valor éxacto, la llenaríamos con

$$101110100_2 = 372$$

Por lo general, si una entrada contiene el número $000000000_2 = 0$, indica que la cuadrícula queda en estado imposible, pero si cada entrada contiene un número con un solo bit activado (es decir, una potencia de dos) la cuadrícula queda solucionada!

Aquí esta un diagrama de flujo para resumir el funcionamiento de sudokuSolver y makeGuess:

Algunas optimizaciones

Nuestro profe de CS241 nos ha regalado un conjunto de $95$ rompecabezas (todos solucionables) para probar nuestro código. Mi algoritmo ingenuo tarda $34.48$ segundos en solucionar todos, así que $0.34$ por segundo por promedio. Además he resumido la distribución de duraciones para todos los rompecabezas en este histograma:

Como manera alternativa de visualizar la distribución de duraciones, aquí está un gráfico de distribución cumulativa:

(El programa que resuelve los Sudoku está escrito en C, pero uso Python para manipular y visualizar los datos sobre su rendimiento.) También he añadido unas líneas a mi código para registrar la "profundidad" de cada rompecabezas - o sea, el número de llamadas anidadas de makeGuess que el algoritmo tiene que realizar. Se puede interpretar la "profundidad" como medida de la dureza del rompecabezas, porque los rompecabezas más difíciles tienden a requerir más adivinación. (Pero no debemos asumir que el algoritmo esté seleccionando sus suposiciones tan eficientemente como un solucionador humano - ya veremos que su manera de adivinar es bastante subóptimo.) Aquí están dos histogramas más - el rojo mide la "profundidad máxima" de cada rompecabezas, es decir, el punto más profundo que alcanza a lo largo del programa; y el azúl mide la profundidad al momento de encontrar una solución:

Y ahora, ¡a optimizar! Tras un poco de experimentación he descubierto dos puntos débiles en mi algoritmo que lo ralentizan:

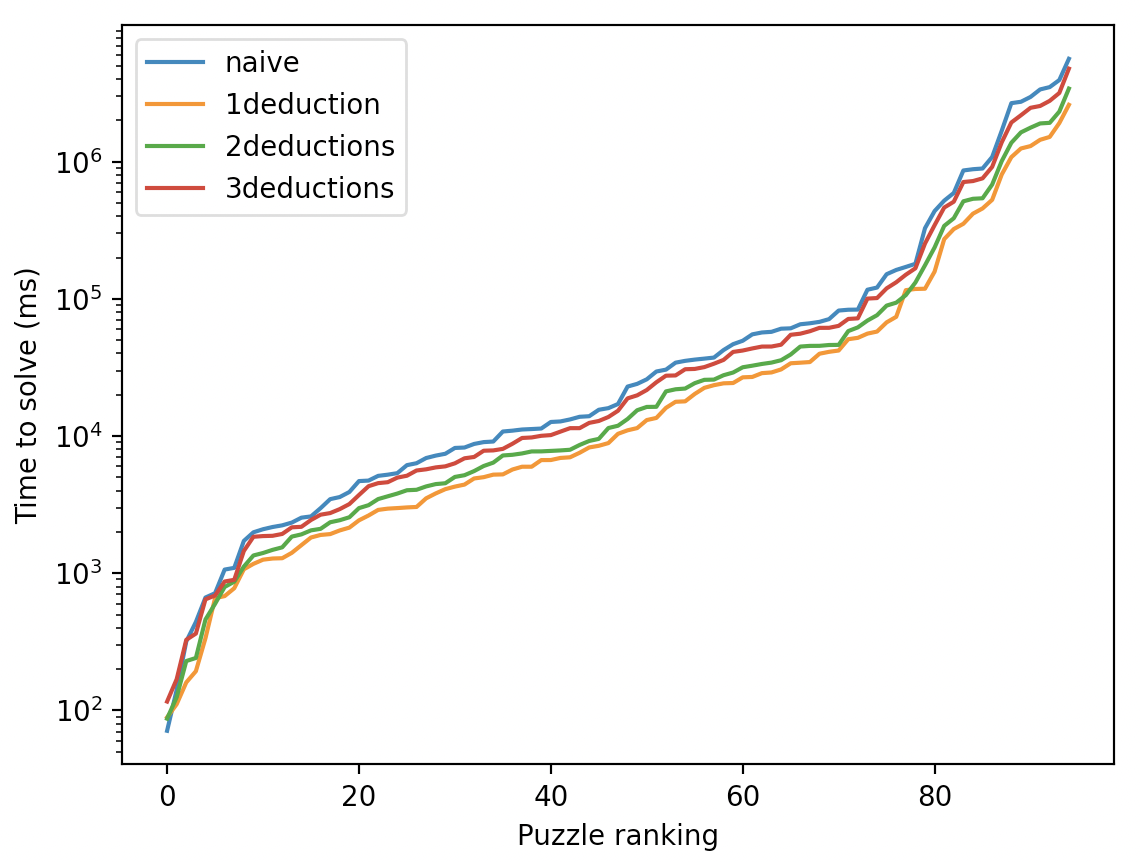
1. El algoritmo llama a la función eliminateEntries hasta que ya no tiene efecto en las entradas de la cuadrícula. Sucede que eso es much más que lo necesario - en contra a la intuición, a veces es más eficiente seguir a llamar a makeGuess sin asegurar que hemos hecho todas las eliminaciones posibles.
2. Al hacer una adivinación, es más ventajoso enfocarse en una entrada con pocas posibilidades, para poder eliminarlas más rápidamente. Por ejemplo, elegir una entrada con $9$ posibilidades dividiría el árbol de posibilidades en $9$ ramales más, pero un entrada con $2$ posibilidades sólo nos dejará dos ramas más para explorar. Después de hacer varias suposiciones, el número de posibilidades se multiplica de manera exponencial - y aún $4^n$ y $3^n$ se crecen mucho más rápidamente que $2^n$.

Para reparar debilidad $1$, modifiqué el algoritmo para llamar a eliminateEntries un número fijo de veces en vez de repetirlo hasta que no tenga efecto. Aquí está una tabla de los resultados:

$$\begin{array}{c|c} \text{Algorithm} & \text{Average time per puzzle} \\\hline \text{Naive} & 0.345 \\ \text{1 call} & 0.163\text{s} \\ \text{2 calls} & 0.208\text{s} \\ \text{3 calls} & 0.284\text{s} \\ \end{array}$$

Y para ver más detalle, otro gráfico que compara las distribuciones cumulativas:

Sorprendente, ¿no? Sea el Sudoku lo que sea, es casi siempre más ventajoso llamar a eliminateAllEntries una sola vez. Tal vez no debe ser tan inesperado ese hallazgo, puesto que cada entrada tiene $20$ "vecinos" (o sea, entradas que comparten la misma fila, columna, o minicuadrícula) y hay $81$ entradas en una cuadrícula, hechos que implican que una sola llamada a eliminateAllEntries involucra $20\cdot 81 = 1620$ eliminaciones a lo máximo, muchos de los cuales serán superfluos.

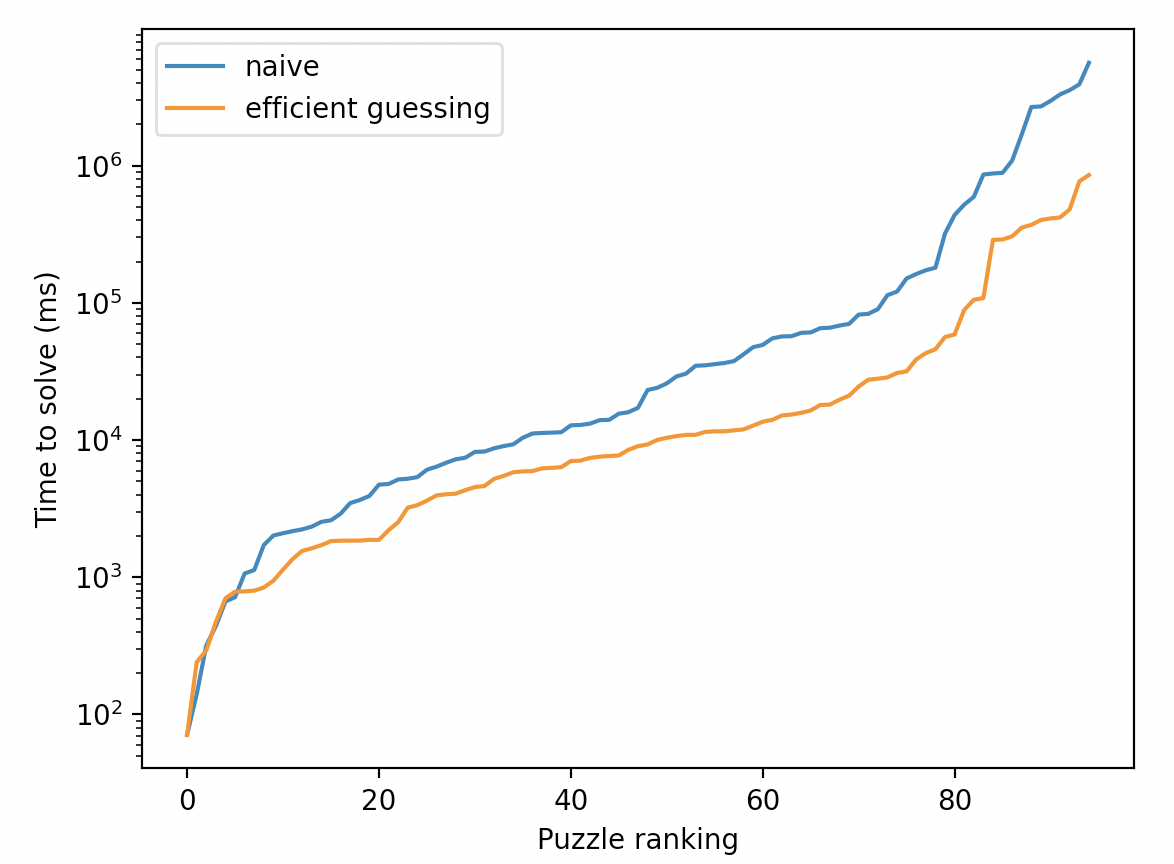
Y ahora a encargarnos de la debilidad $2$. En vez de simplemente elegir la primera entrada todavía no determinada al llamar makeGuess, debemos comenzar con buscar entradas con sólo dos posibilidades, y si no hay, buscar entradas con tres, etcétera. Esta revisión otorga una mejora significante - ¡resuelve los $95$ Sudoku en $6.13$ segundos, tardando $0.061$ segundos por Sudoku por promedio! Esta modificación sencilla casi ha acelerado nuestro "algoritmo ingenuo" por un factor de $5$. Aquí están los gráficos de distribución cumulativa otra vez, para comparar:

Al fin, comparamos el rendimiento de los siguiente cuatro versiones del algoritmo:

• El algoritmo original "ingenuo
• El algoritmo con sólo debilidad $1$ reparado
• El algoritmo con sólo debilidad $2$ reparado
• El algoritmo con ambas debilidades reparadas

Aquí esta una tabla que los compara:

$$\begin{array}{c|c} \text{Algorithm} & \text{Average time per puzzle} \\\hline \text{Naive} & 0.345 \\ \text{Elimination optimized} & 0.163\text{s} \\ \text{Guessing optimized} & 0.061\text{s} \\ \text{Both optimized} & 0.030\text{s} \\ \end{array}$$

Y aquí el gráfico de distribución cumulativa:

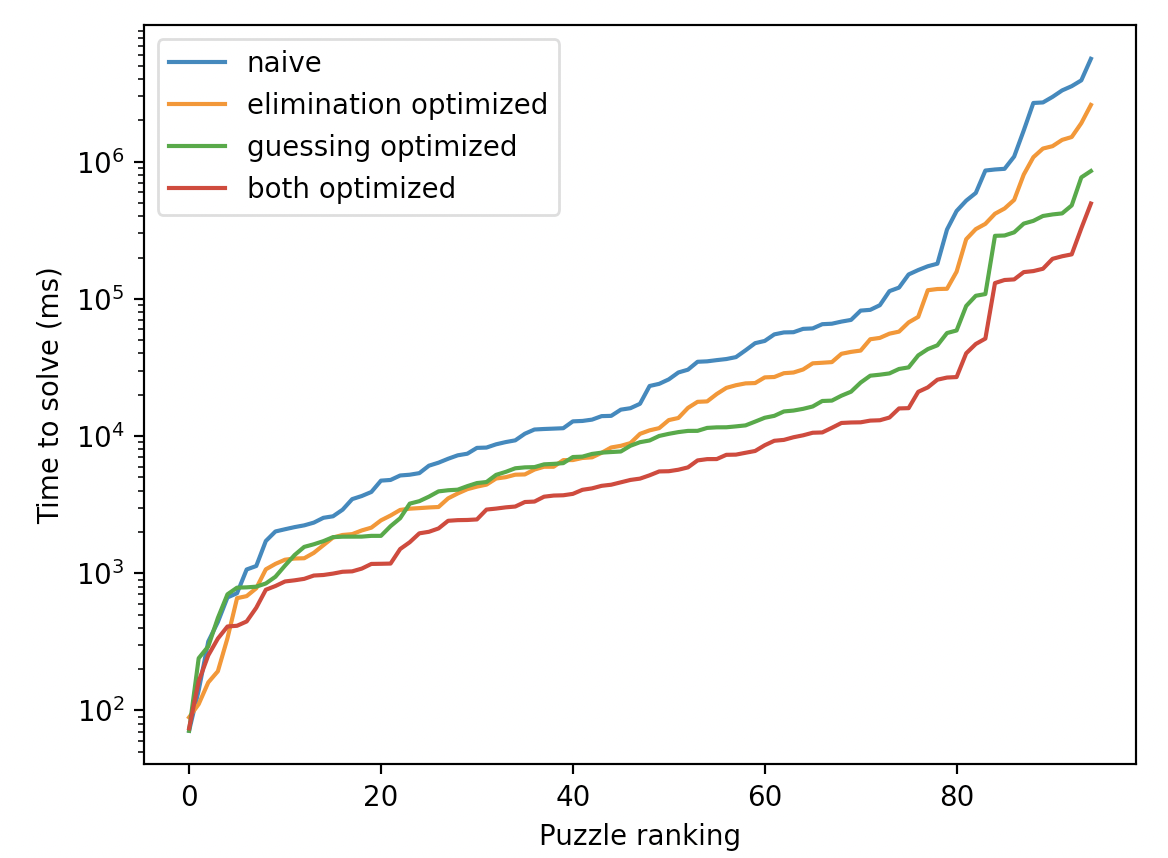
Observamos que, para los Sudoku menos difíciles (los que requieren menos tiempo, que caen en el lado izquierda del gráfico) ni el algoritmo optimizado para eliminación ni lo optimizado para adivinación supera el otro. Por otro mano, para los Sudoku más difíciles, vemos que la optimización de adivinación es más importante. Eso explica cómo la optimización de adivinación ha influido el promedio de las duraciones de manera tan extrema: ha reducido las duraciones necesarias para los Sudoku más engorrosos que iban ejerciendo una influencia más fuerte sobre el promedio que los otros, por ser más caros por varios factors de $10$.

Conclusión

Seguramente podría optimizar mi algoritmo aún más a través de varios ajustes, por ejemplo:

• Llamar a eliminateAllEntries aún menos, tal vez ni siquiera cada vez que sudokuSolver está llamado
• Revisar eliminateAllEntries para eliminar redundancia, o sea asegurar que no desempeña la misma eliminación varias veces, o detenerse en medio de su funcionamiento al toparse con una imposibilidad
• Al elegir entradas para adivinar, priorizar no sólo las entradas con menos posibilidades, sino también las que tienen mayor cantidad de vecinos no determinados (para maximizar el "impacto" de la adivinación)

Si a tí te gustaría juguetear con mi código, lo adjuntaré aquí tan pronto que el proyecto de CS241 vence (para no dejar por accidente que alguien copie mi solución).

Al fin, aquí están algunas preguntas interesantes para meditar:

¿Como máximo, cuántas entradas llenas puede tener un Sudoku que tiene solución no única?
¿Puedes concebir una cota superior del número de suposiciones necesarias para resolver un Sudoku que tiene solución única?
¿Cómo escribirías un algoritmo para determinar el número de soluciones posibles a un Sudoku que no necesariamente tenga solución única?
¿Cómo escribirías un algoritmo para diseñar un rompecabezas de Sudoku? ¿Para asegurar que su solución sea única? ¿Para ajustar su dificultad?
¿Si llenas $n$ entradas de una cuadrícula aleatoriamente, cuál es la probabilidad de que exista una solución? ¿Y qué tal una solución única?