Skip to page content Home     Einträge     Lebenslauf     Kontakt     Leute     RSS

Intransitive Zufallsvariablen

(Psst! Don't want to read this in German? Here's a translation.)

Stell dir vor, ein Schwindler schlagt vor, ein einfache Würfelspiel zu spielen, in dem es drei Würfel gibt, jeder spieler würfelt einen von denen und der, der die höchste Zahl erhält, wird der Sieger. Aber um dich daran zu beruhigen, daß es keinen gezinkten Würfel gibt, der höhere Zahlen als die anderen in den meisten Fällen hervorbringt, der Schwindler schenkt dir die Gelegenheit, den Würfel auszuwählen, der dir am meisten gefällt, vor er den Seinen wählt.

Vielleicht ahnst du irgendeine Art von Betrügerei, aber wenn du das Recht der ersten Wahl hast, denkst du, das Spiel gerecht sein könnte, oder sogar zu deinem Vorteil? Und wenn die drei Würfel sind die Folgenden?

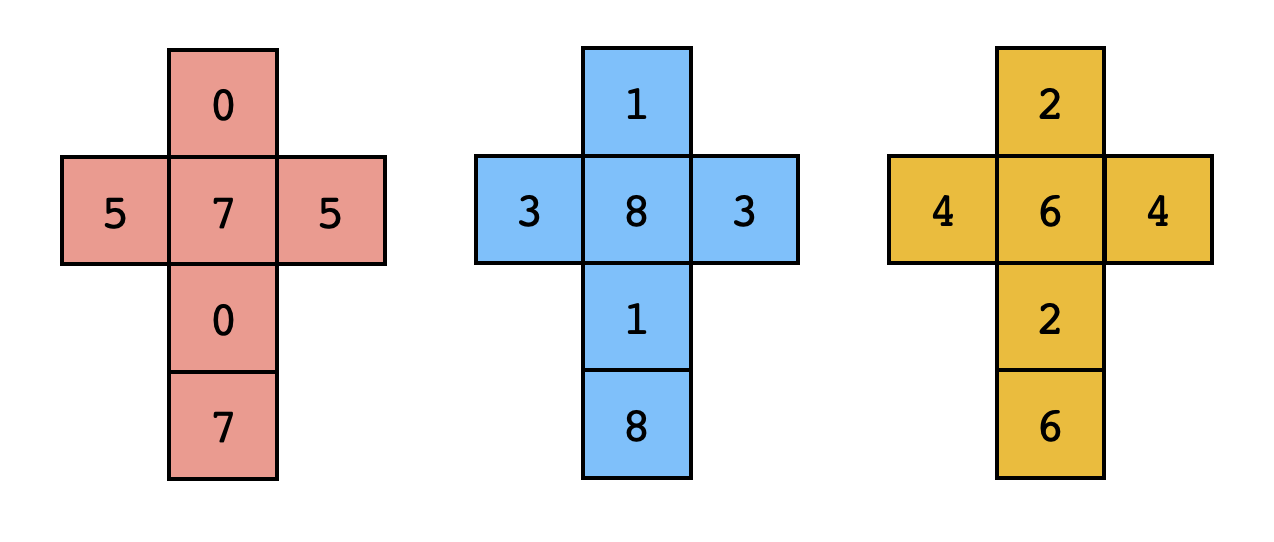
Als drei Zufallsvariablen könnte man diese drei Würfel formulieren:

$$\begin{align*}X &= \begin{cases}0 & \text{Wahrscheinlichkeit } 1/3 \\ 5 & \text{Wahrscheinlichkeit } 1/3 \\ 7 & \text{Wahrscheinlichkeit } 1/3 \end{cases} \\ Y &= \begin{cases}1 & \text{Wahrscheinlichkeit } 1/3 \\ 3 & \text{Wahrscheinlichkeit } 1/3 \\ 8 & \text{Wahrscheinlichkeit } 1/3 \end{cases} \\ Z &= \begin{cases}2 & \text{Wahrscheinlichkeit } 1/3 \\ 4 & \text{Wahrscheinlichkeit } 1/3 \\ 6 & \text{Wahrscheinlichkeit } 1/3 \end{cases}\end{align*}$$

Diese drei Zufallsvariablen entsprechen einer seltsamen Eigenschaft - fallweise kann man bestätigen, daß

$$\begin{align*}\mathbb P(X < Y) &= 5/9 \\ \mathbb P(Y < Z) &= 5/9 \\ \mathbb P(Z < X) &= 5/9\end{align*}$$

Das ist, es gibt keinen besten Würfel aber egal ist das Spiel kein gerechtes Spiel. Für jeden Würfel entspricht ihm anderen Würfel, die eine höhere Zahl in den meisten Fällen hervorbringt. Egal, welchen Würfel wählst du, wird der Schwindler einen erwählen um das Spiel mit Wahrscheinlichkeit $5/9$ zu gewinnen.

Aufklärung des Paradoxes

Dieses Phänomen heißt Intransitivität der Zufallsvariablen und es ist manchmal für seine unintuitive Natur bekannt. In diesem Abteil möchte ich einen generelleren Sachverhalt betreten, der (meiner Ansicht nach) auf den Grund, dieses Phänomen uns so verwirrend erscheinen kann, ein bisschen Licht wirft.

Stell mal vor, wir überlegen drei Sätze $\psi,\phi,\chi$ die wahr oder falsch für jede Ergebnis der Zufallsvariable $W$ sind. Das ist, wenn $\Omega$ das Ergebnismenge der Zufallsvariable $W$ ist, denn sind $\psi,\phi,\chi$ Prädikaten aus der Menge $\Omega$. Wenn zwei Prädikaten $\psi,\phi$ inkompatibel sind, oder anders gesagt $\neg(\psi\land\phi)$ in jedem Fall Wahr wird, dann folgt es, daß $$\mathbb P(\psi) + \mathbb P(\phi) \leq 1$$ Stell aber mal vor, daß $\psi, \phi, \chi$ unvereinbar sind, also, daß $$\neg(\psi\land\phi\land\chi)$$ Zum Beispiel wenn $W$ aus einem Tripel von Zufallvariablen $(X,Y,Z)$ besteht sind die drei Aussagen $$\begin{align*}\psi &= \mathtt{"X < Y"} \\ \phi &= \mathtt{"Y < Z"} \\ \chi &= \mathtt{"Z < X"}\end{align*}$$ unvereinbar, aber jetzt sprechen wir über Prädikaten im allgemeinen. Intuitiv könnte es den Anschein haben, wir könnten genauso die Ungleichung $$\mathbb P(\psi) + \mathbb P(\phi) + \mathbb P(\chi) \leq 1$$ ableiten und zur Folge ableiten, daß es nicht sein könnte, jeder der drei Wahrscheinlichkeiten $\mathbb P(\psi),\mathbb P(\phi),\mathbb P(\chi)$ größer als $1/3$ sei, also $$\min\Big(\mathbb P(\psi),\mathbb P(\phi),\mathbb P(\chi)\Big) \leq \frac{1}{3}$$ und daß wenn $\Omega$ optimal verteilt wäre, um diese Mindestwahrscheinlichkeit zu maximieren, dann würde es so erscheinen:

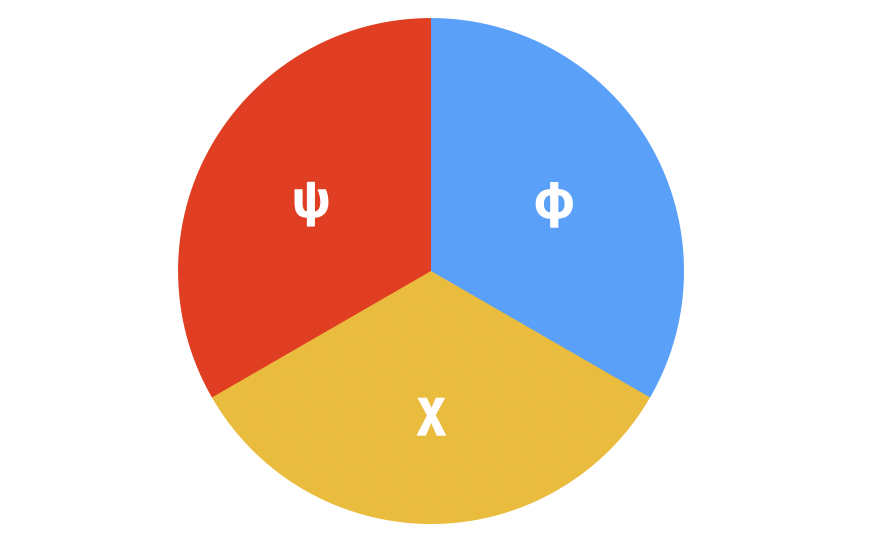
Diese Auswertung ist aber falsch, weil die drei Prädikaten unvereinbar aber nicht paarweise unvereinbar sind. Die Aussage $\psi\land\phi$ könnte wohl wahr sein und genauso können $\phi\land\chi$ oder $\chi\land\psi$ wahr sein, obwohl $\psi\land\phi\land\chi$ immer falsch ist. Für jeder Ergebnis $\omega\in\Omega$ können am meisten zwei von den drei unvereinbaren Prädikaten wahr sein und deshalb kann die Überlagerung der drei Teilmengen $$\psi^{-1}(\mathtt{T}), \phi^{-1}(\mathtt{T}), \chi^{-1}(\mathtt{T})\subset \Omega$$ die Ergebnismenge $\Omega$ am meisten zweifach bedecken. Aufgrund dieser Betrachtung können wir die wahre Obergrenze herleiten: $$\mathbb P(\psi) + \mathbb P(\phi) + \mathbb P(\chi) \leq 2$$ und deshalb $$\min\Big(\mathbb P(\psi),\mathbb P(\phi),\mathbb P(\chi)\Big) \leq \frac{2}{3}$$ und die begrenzende Verteilung wäre etwa so:

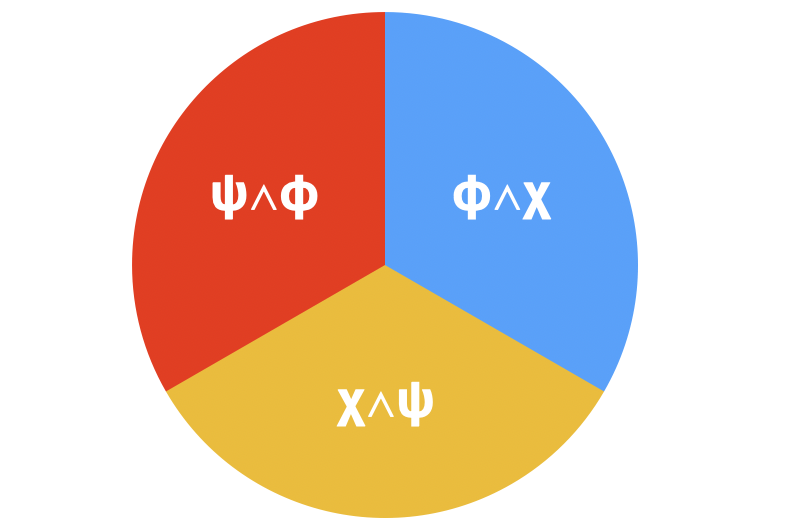
In der Wirklichkeit gibt es deswegen kein Paradox. Meines Erachtens stammt die unintuitive Natur dieses Phänomens von einer schlechten Intuition wenn es um Aussagen derart "wahrscheinlich wird $\psi$ wahr" geht. Im Allgemeinen erfordert es viele geistigen Anstrengung, die folgende Aussagen miteinander abstimmen zu laßen:

• Wahrscheinlich wird $\psi$ wahr.
• Wahrscheinlich wird $\phi$ wahr.
• Wahrscheinlich wird $\chi$ wahr.
• Sicherlich werden $\psi,\phi,\chi$ nicht gleichzeitig wahr.

Mit zwei Prädikaten gibt es kein "Paradox" dieser Art, weil es kann nicht sein, daß von $\psi$ und $\phi$ beide wahrscheinlich seien aber $\psi\land\phi$ unmöglich sei, wenn man die Aussage "wahrscheinlich wird $\psi$ wahr" als $\mathbb P(\psi) > 1/2$ auffaßt.

Maximale Intransitivität

Wir haben schon entdeckt, daß mit drei Zufallsvariablen $X,Y,Z$ es keinen größeren Transitivitätsverstoß als das Folgende geben kann: $$\mathbb P(X < Y) = \mathbb P(Y < Z) = \mathbb P(Z < X) = \frac{2}{3}$$ Umgekehrt kann man einfach bestätigen, daß dieser Transitivitätsverstoß möglich ist, z.B. wenn $X,Y,Z$ die gemeinsame Wahrscheinlichkeitsverteilung befolgen: $$(X,Y,Z) = \begin{cases}(0,1,2) & \text{Wahrscheinlichkeit } 1/3 \\ (1,2,0) & \text{Wahrscheinlichkeit } 1/3 \\ (2,0,1) & \text{Wahrscheinlichkeit } 1/3\end{cases}$$ Doch wir haben auf eine wichtige Bestimmung der Zufallsvariablen verzichtet, damit sie als eine realistische Generalisierung des originalen Würfelspiel gelten, nämlich daß sie unabhängig sind. Offensichtlich sind die drei Zufallsbariablen in der obenen Wahrscheinlichkeitsverteilung abhängig. Es könnte sein, daß man drei unabhängige Zufallsvariablen erfinden kann, daß diese 2/3-Grenze auch erreichen, doch keine solche Beispiele haben wir bis jetzt gesehen.

Stellen Sie vor, eine einfachere Frage, in der man setzt voraus, daß $Y$ eine Konstante sei, also, daß es eine reele Zahle $c$ gäbe, derart $\mathbb P(Y = c) = 1$. Wir setzen auch voraus, daß die Wahrscheinlichkeit, irgendeine zwei der drei Variablen zeigen sich gleich, sei null. In diesem Fall sucht man den Größtwert der Mindestwahrscheinlichkeit $$\min\Big(\mathbb P(X < c), \mathbb P(c < Z), \mathbb P(Z < X)\Big)$$ wenn $X,Z$ unabhängig sind. Es gilt aber dann, daß $$\mathbb P(Z < X) \leq 1 - \mathbb P(X < c) \mathbb P(c < Z)$$ weil $X < c$ und $c < Z$ zusammen auf $X < Z$ schließen laßen, und die zwei Möglichkeiten unabhängig sind (aufgrund dieser Voraussetzung können wir seine Wahrscheinlichkeiten multiplizieren). Deshalb ist den ersuchten Größtwert höchstens $$\max_{p,q\in [0,1]} \min\big(p,q,1-pq\big)$$ Man kann aber überprüfen, daß diese Minimalwert am höchsten steigt wenn $p=q=1-pq$ also wenn $$p=q=\frac{1}{\phi}=\frac{-1+\sqrt{5}}{2}\approx 0.618$$ Deshalb wissen wir, wenn $Y$ konstante ist, daß wir einen Maximaltransitivitätsverstoß von $\phi^{-1}\approx 0.618$ erreichen könnten, doch ob es wirklich erreichbar ist wissen wir noch nicht. Sogar kann man von dieser Spezialfallgrenze eine generelle Grenze ableiten: in dieser Schrift von S. Trybula wird es bewiesen, daß der Maximaltransitivitätsverstoß $\phi^{-1}$ ist, auch wenn $Y$ nicht konstant sein kann. Das ist: $$\min\Big(\mathbb P(X < Y), \mathbb P(Y < Z), \mathbb P(Z < X)\Big) \leq \phi^{-1}$$

Es ist ein schönes Rätsel rausfinden, ob es zwar drei unabhängige Zufallsvariablen gibt oder nicht, die diese Obergrenze erreichen. Tatsache ist, daß ein solches Tripel existiert und zwar existiert ein Tripel in dem $Y$ konstant ist: $$\begin{align*}X &= \begin{cases}1 & \text{Möglichkeit } \phi^{-1} \\ 4 & \text{Möglichkeit } \phi^{-2}\end{cases} \\ Y &= 2 \\ Z &= \begin{cases}0 & \text{Möglichkeit } \phi^{-2} \\ 3 & \text{Möglichkeit } \phi^{-1}\end{cases}\end{align*}$$ Gleich könnte man diese Zufallsvariablen durch ihre Wahrscheinlichkeitsdichtefunktionen beschreiben: $$\begin{align*}p_X(\alpha) &= \tfrac{1}{\phi}\delta_1(\alpha) + \tfrac{1}{\phi^2}\delta_4(\alpha) \\ p_Y(\alpha) &= \delta_2(\alpha) \\ p_Z(\alpha) &= \tfrac{1}{\phi^2}\delta_0(\alpha) + \tfrac{1}{\phi}\delta_3(\alpha)\end{align*}$$ und etwa so visualisieren:

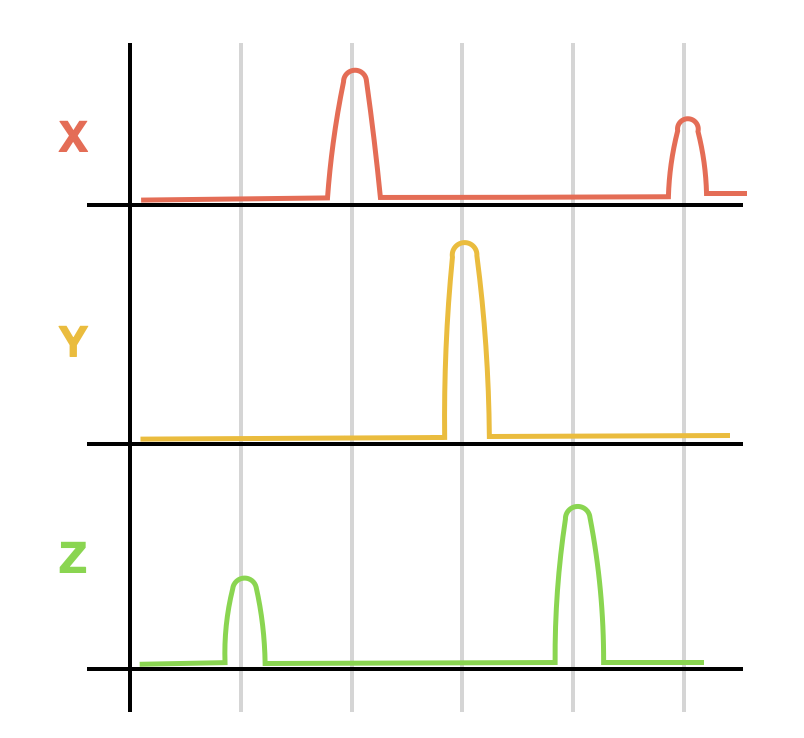
Wenn es um vier oder mehr Zufallsvariablen gibt bin ich mir nicht sicher, wieviel der Maximaltransitivitätsverstoß wäre. Mit mehrere Zufallsvariablen kann man die Obergrenze $\phi^{-1}$ überschreiten aber es läßt sich ziemlich einfach beweisen, daß es eine universale Obergrenze von $3/4$ gibt, das ist, wenn $X_1,X_2,\cdots, X_n$ unabhängige Zufallsvariablen sind, dann muss es sein, daß $$\min\Big(\mathbb P(X_1 < X_2), \cdots, \mathbb P(X_n < X_1)\Big)\leq \frac{3}{4}$$ Kannst du diese Obergrenze beweisen? Wenn du ein Hinweis möchtest, würde ich dir andeuten, es könnte günstig sein, Mediane der $n$ Zufallsvariablen überzulegen.

Parametrisierung einer Familie von intransiitiven Zufallsvariablen

Nehmen wir mal an, daß wir drei Zufallsvariablen $X,Y,Z$ haben, und daß wir eine ganze Familie von Zufallsvariablen so bestimmen: $$W(p,q,r) = \begin{cases}X & \text{Wahrscheinlichkeit } p \\ Y & \text{Wahrscheinlichkeit } q \\ Z & \text{Wahrscheinlichkeit } r\end{cases}$$ wenn $p+q+r=1$. Das ist, $W(p,q,r)$ heißt ein Zufallsvariabel, der sein Wert von $X$ nimmt mit Wahrscheinlichkeit $p$, von $Y$ mit Wahrscheinlichkeit $q$ und von $Z$ mit Wahrscheinlichkeit $r$. Anders gesagt, wenn $f_X,f_Y,f_Z$ die Wahrscheinlichkeitsdichtefunktionen von $X,Y,Z$ bzw. sind, dann wird die Wahrscheinlichkeitsdichtefunktion von $W(p,q,r)$ $$pf_X + qf_Y + rf_Z$$ Wir könnten diese Familie von Zufallsvariablen als dreidimensionale Vektoren von $\mathbb R^3$ parametrisieren: $$W(p,q,r) ~ \leftrightarrow ~ \begin{bmatrix}p \\ q \\ r\end{bmatrix}$$ Wenn man die Parameter $p,q,r$ beziehungsweise alle mögliche Werten der Interval $[0,1]$ bekommen laßen, derart $p+q+r=1$, dann manifestiert sich der Raum aller möglichen Zufallsvariablen dieser Familie als ein Dreieck in $\mathbb R^3$:

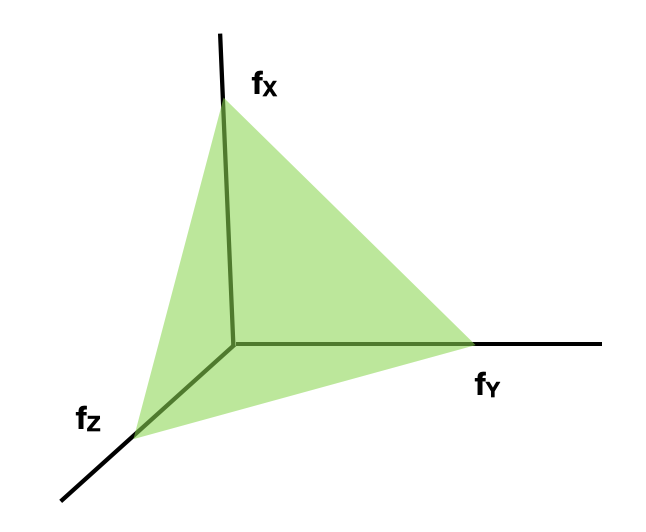
Um ganz exakt zu sein, wir beschreiben eine Einbettung der konvexe Hülle der drei Funktionen $f_X,f_Y,f_Z$ im Vektorraum alle Distributionen auf $\mathbb R$ in dem dreidimensionalen Vektorraum $\mathbb R^3$ mittels eine konvexkombinationstreue Abbildung. Bitte beachte, daß die Zufallsvariablen $W(1,0,0), W(0,1,0), W(0,0,1)$ sind gleich verteilt wie $X,Y,Z$ beziehungsweise und den Ecken des Dreiecks entsprechen.

Wenn wir noch mal annehmen, daß die drei Zufallsvariablen $X,Y,Z$ mit Wahrscheinlichkeit $1$ verschiedene Werte hervorbringen, und wenn wir die drei Wahrscheinlichkeiten $$\begin{align*}&\mathbb P(X < Y) \\ &\mathbb P(Y < Z) \\ &\mathbb P(Z < X)\end{align*}$$ wissen, dann können wir die Wahrscheinlichkeit jeder Vergleichung von zwei Zufallsvariablen unserer Familie $W(p,q,r)$ berechnen, also, die Wahrscheinlichkeit $$\mathbb P\Big(W(p_0,q_0,r_0) < W(p_1,q_1,r_1)\Big)$$ kalkulieren. Die Parametrisierung dieser Zufallsvariablen als Vektoren wird uns sehr nützlich, um diese Wahrscheinlichkeit einfach zu formulieren: wenn $\mathbf{w}_0, \mathbf{w}_1$ die Vektoren, die $W(p_0,q_0,r_0)$ und $W(p_1,q_1,r_1)$ bzw. entsprechen, und $A$ die Matrix $$A = \begin{bmatrix}\mathbb P(X < X') & \mathbb P(X < Y') & \mathbb P(X < Z') \\ \mathbb P(Y < X') & \mathbb P(Y < Y') & \mathbb P(Y < Z') \\ \mathbb P(Z < X') & \mathbb P(Z < Y') & \mathbb P(Z < Z')\end{bmatrix}$$ ist, dann kann man fallweise beweisen, daß $$\mathbb P\Big(W(p_0,q_0,r_0) < W(p_1,q_1,r_1)\Big) = \mathbf{w}_0^{\text{T}}A\mathbf{w}_1$$

Endlich bedenken wir den Fall, in dem $X,Y,Z$ drei unabhängige Zufallsvariablen die die Transitivität maximal missachten sind. Dann wird $$A = \begin{bmatrix}1/2 & 1/\phi & 1/\phi^2 \\ 1/\phi^2 & 1/2 & 1/\phi \\ 1/\phi & 1/\phi^2 & 1/2\end{bmatrix}$$ Merke: wir können $A$ anders beschreiben als $$A = \tfrac{1}{2}I + \tfrac{1}{\phi}C + \tfrac{1}{\phi^2}C^2$$ in der $C$ die Permutationsmatrix $$C = \begin{bmatrix}0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0\end{bmatrix}$$ bezeichnet. Und diese Matrix, als lineare Abbildung des Vektorraum $\mathbb R^3$, permutiert die drei Koordinaten der Vektoren, oder es führt eine Drehung von $2\pi/3$ um den Vektor $\langle 1,1,1\rangle$ durch:

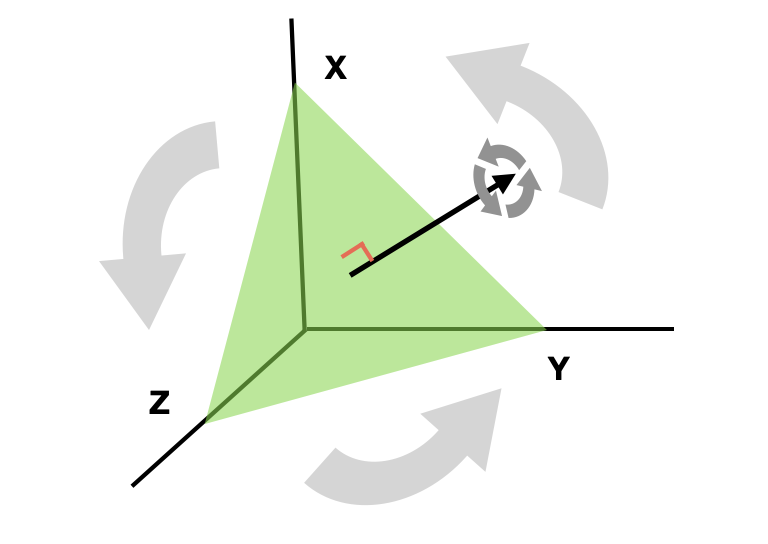
Was sehr interessant ist, ist daß $C$ ein Spezialfall der generellen Rotationsmatrix $R_\theta$ um den Vektor $\langle 1,1,1\rangle$ im Gegenuhrzeigersinn ist, sodass $C=R_{2\pi/3}$. Alle Rotationsmatrizen um die gleichen Achse laßen sich vertauschen weil $R_{\theta_0} R_{\theta_1} = R_{\theta_0 + \theta_1}$, deshalb $$CR_\theta = R_\theta C$$ für jede $\theta$. Zur Folge, jede $R_\theta$ sich mit $A$ vertauschen läßt, weil $$\begin{align*}R_\theta A &= \Big(\tfrac{1}{2}I + \tfrac{1}{\phi}C + \tfrac{1}{\phi^2}C^2\Big)A \\ &= \tfrac{1}{2}IA + \tfrac{1}{\phi}CA + \tfrac{1}{\phi^2}C^2 A \\ &= \tfrac{1}{2}AI + \tfrac{1}{\phi}AC + \tfrac{1}{\phi^2}AC^2 \\ &= AR_\theta\end{align*}$$ Deshalb wird die Möglichkeit des Ergebnis $W_0 < W_1$, wenn wir die Vektoren der Parameter $\mathbf w_0, \mathbf w_1$ sich $\theta$ Radianten in der Ebene $x+y+z=1$ drehen laßen, also, sich mit $R_\theta \mathbf w_0, R_\theta \mathbf w_1$ ersetzen laßen, weil $$\begin{align*} (R_\theta \mathbf w_0)^\text{T} A (R_\theta \mathbf w_1) &= \mathbf w_0^\text{T} R_\theta^\text{T} A R_\theta \mathbf w_1 \\ &= \mathbf w_0^\text{T} R_{-\theta} A R_\theta \mathbf w_1 \\ &= w_0^\text{T} R_{-\theta} R_\theta A \mathbf w_1 \\ &= w_0^\text{T} A \mathbf w_1 \end{align*}$$ Tatsächlich kann man die Wahrscheinlichkeit $\mathbb P(W_0 < W_1)$ kalkulieren auch wenn man nur die Größe der Komponenten und den Wert des Winkels zwischen den Komponenten der Vektoren $\mathbf w_0, \mathbf w_1$ in der Ebene $x+y+z=1$. Wenn seine Projektionen auf diese Ebene Größe $r_0, r_1$ haben und einen Winkel $\Delta\theta$ im Gegenuhrzeigersinn miteinander bilden, etwa so:

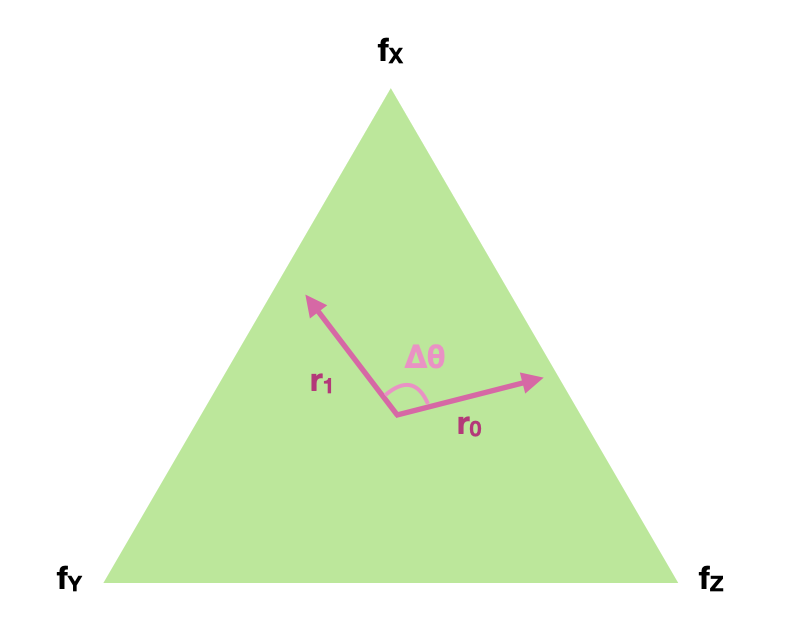
dann wird $\mathbb P(W_0 < W_1)$:

$$\frac{1}{2}+r_1 r_2\Big(\tfrac{1}{2}\cos(\Delta\theta) + \tfrac{1}{\phi}\cos\big(\Delta\theta + \tfrac{2\pi}{3}\big)+ \tfrac{1}{\phi^2}\cos\big(\Delta\theta + \tfrac{4\pi}{3}\big)\Big)$$

Also, wenn man eine längere Kette von Zufallsvariablen $X_1, \cdots, X_n$ aufbauen will, die intransitiv sind, derart, daß $$\mathbb P(X_0 < X_1) = \cdots = \mathbb P(X_n < X_0) > \frac{1}{2}$$ könnte man einfach $n$ Vektoren in diesem Dreiecke finden, die die gleiche Länge haben und kongruenten Winkeln bzw. formen. Zum Beispiel, wenn man die $5$ Zufallsvariablen betrachtet, die den Vektoren $$\begin{align*}\mathbf w_0 &= \langle 0.5, 0.5, 0\rangle \\ \mathbf w_1 &= R_{-2\pi/5}\mathbf w_0 \\ \mathbf w_2 &= R_{-4\pi/5}\mathbf w_0 \\ \mathbf w_3 &= R_{-6\pi/5}\mathbf w_0 \\ \mathbf w_4 &= R_{-8\pi/5}\mathbf w_0\end{align*}$$ oder

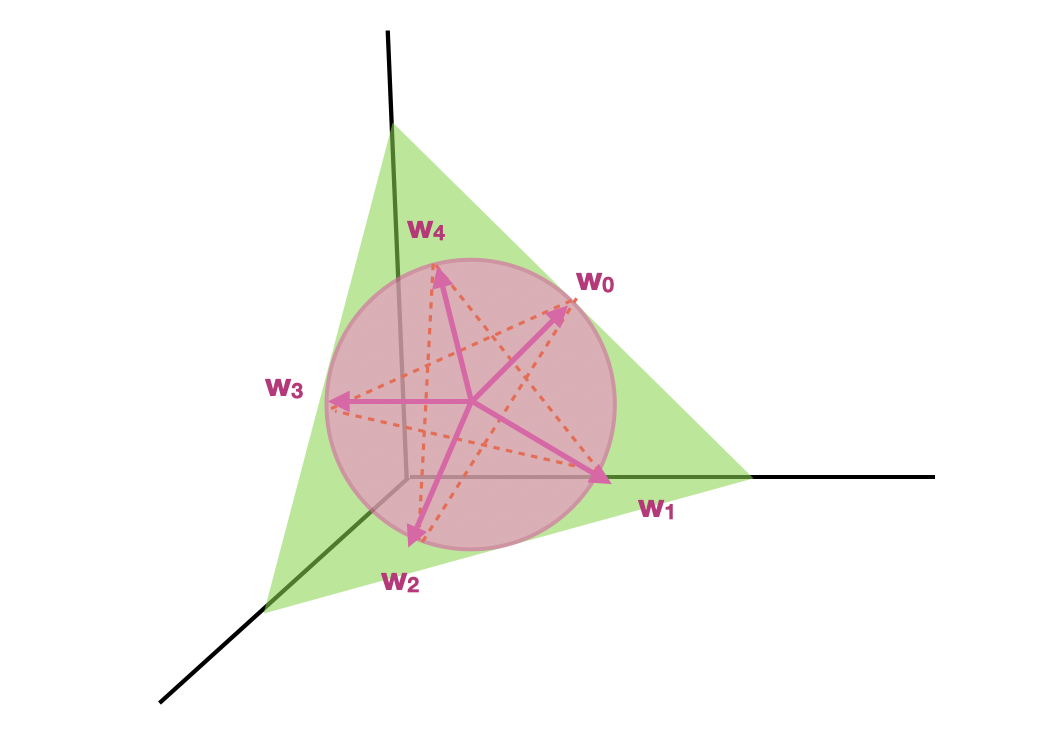
entsprechen, denn bekommt man einen (kleinen aber nicht nightigen) Transitivitätsverstoß von $\approx 0.532$, das ist, die Minimalwahrscheinlichkeit von $\mathbb P(W_0 < W_1), \cdots, \mathbb P(W_4 < W_0)$ wird $\approx 0.532$. Vermittels diese geometrische Visualisierung kann man größere und komplexere Familien von intransitiven Zufallsvariablen aufbauen, obwohl sie in den meisten Fällen nicht optimal sind.

The posts on this website are licensed under CC-by-NC 4.0.