
As with so many of my blog posts, this post is written more or less for my former self. The first time I tried setting up a Raspberry Pi, I didn't have any external monitor to connect to the Pi, and I was frustrated to find that many of the online tutorials for setting up your RPi presuppose this. Through more targeted googling and trial and error I was able to get a remote shell on my RPi without any external monitor or keyboard.
This post is basically a write-up of my personal notes on how to accomplish this, with some additional tips explaining how you can connect to your RPi from outside of your private home network. If I go a few months without touching my RPi and then end up having to set it up again, I'll probably refer back to this post myself!
Here's exactly what you need to follow this tutorial:
First, you should download the Raspberry Pi Imager from the Raspberry Pi website. You'll use this to load an operating system onto the micro-SD card. Consult the specs of your RPi to determine its model, and whether it is 64-bit or 32-bit. My RPi was purchased from here, so it's a Raspberry Pi 4 with 64-bit architecture. Connect the micro-SD card to your PC and open up the Raspberry Pi Imager. Then select the correct model and the appropriate version of Raspbian (the dedicated Linux distribution for RPis) for your architecture, select the micro-SD card as your storage, and proceed to the next step.

You may be prompted to apply "OS customisation settings". If so, you should select "edit settings". In this menu, you can set a username and password for an account on the RPi. If your home network is wireless, you should enter the SSID and password for your home WiFi, so that the RPi can connect automatically to WiFi when it starts up. You can also set a hostname. Even if you don't change the hostname, you should copy it down somewhere, because it will be useful for connecting to the RPi momentarily. Here's what my settings look like:
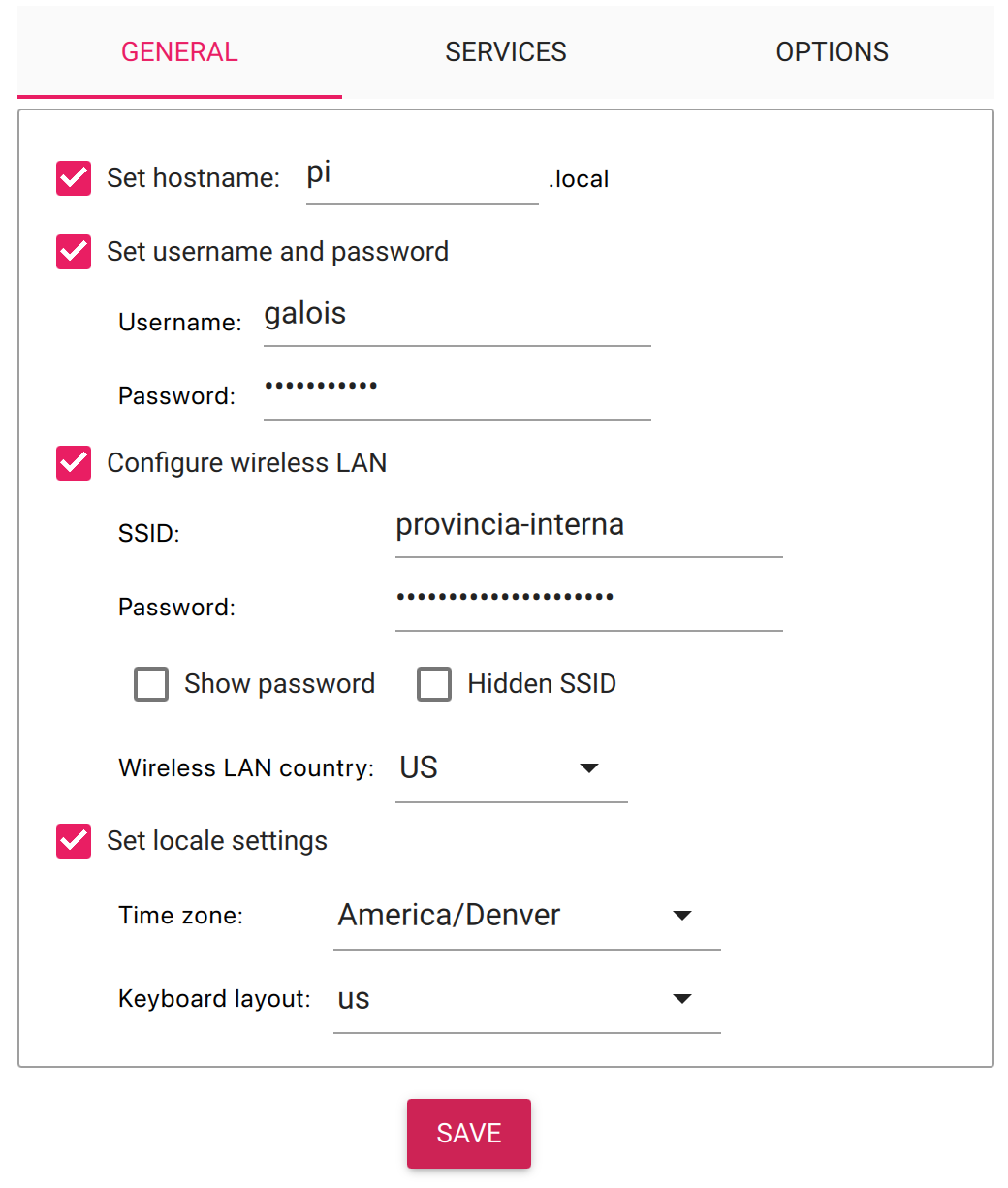
Under the "services" heading, you should also ensure that "enable SSH" is turned on. SSH is the application that we'll use to get a command shell on the RPi without physically connecting a keyboard and monitor to it. For now, it's okay to use the password authentication option. But more on this in a second.
Then, you can go ahead and flash the OS onto the micro-SD card. This could take a few minutes. When that's finished, remove the micro-SD card, insert it into the RPi and power it on. If your home network is wired, plug one end of an ethernet cable into your RPi and the other end into your home router. It may take a couple of minutes to start up for the first time and connect to the network.
Now, try running ping pi.local from a terminal on your PC. If you get a response, that's great! Then you should (hopefully) be able to get shell access to the RPi by running ssh [email protected] (replacing galois with your chosen username).
If your RPi responded to a ping, but you weren't able to connect to it via ssh, the tips in this section aren't applicable to you. But if it didn't even respond to a ping, keep reading.
If your RPi doesn't respond to a ping pi.local from your PC, a number of things may be wrong. Here are some possibilities (but I'm sure there are others).
pi.local with your RPiLet's start with the easiest one. Make sure that the hostname you jotted down from the OS configuration screen is the same one you're trying to ping.
Then make sure that the network your PC is connected to is the same as the network that your RPi is connected to. If the network is wired, they should be connected to the same router via two separate ethernet cables. If it's wireless, then the name (SSID) of the WiFi network that your PC is connected to should be the same as the name of the wireless network that you entered on the OS customization screen. If the ping still doesn't work, then continue.
In the past, I've had trouble getting my RPi to connect to my WiFi just by filling out the settings on the "OS customization" menu. However, the tip mentioned in this tutorial has worked for me, despite the fact that it's no longer officially supported since the Bookworm version of Debian - so you might also try it out for yourself, if your network is wireless. Create a text file called wpa_supplicant.conf, entering the SSID and password for your own home network:
country=US
ctrl_interface=DIR=/var/run/wpa_supplicant GROUP=netdev
update_config=1
network={
scan_ssid=1
ssid="YOUR-HOME-SSID-HERE"
psk="YOUR-WIFI-PASSWORD-HERE"
}
Open the micro-SD card up on your PC again, and place a copy of this text file into the card's boot folder. Then insert it back into the RPi, power it on, and wait a few minutes before trying again.
If all of this still doesn't work, it's possible that your RPi was actually connecting to the network all along, but your PC was unable to resolve the hostname pi.local. Hostnames ending in .local are propagated using a protocol called Multicast DNS (mDNS). If there's a problem with mDNS on your PC, it may not be able to associate the name pi.local with the IP address of your RPi.
However, you don't need the hostname to connect to your RPi, and you may be able to figure out its IP address by other means. If you can access an admin portal for your router, you may be able to see a list of connected hosts there, and identify one of them as your RPi. If not, you may still be able to ascertain the RPi's IP address through a bit of detective work. You can run the command arp -a on your PC to view a list of the IP (and MAC) addresses of devices on the same subnet. Power down your RPi and run arp -a on your PC, copying down the IP addresses that appear in the output. Then turn your RPi back on, wait a couple of minutes, and run arp -a again. If any new IP address is present the second time, it's possible that it belongs to your RPi!
If you're having trouble connecting to your RPi over SSH, first make sure that you can ping it, as described above. If you cannot ping your RPi, then there is no network connectivity between your RPi and your PC, and no amount of SSH troubleshooting will save you. But if the ping step succeeds and the SSH connection fails,
If you're unable to login over SSH, make sure that you have the correct password, and that you enabled password authentication during the OS customization step. If this still doesn't work, there is another hack for enabling SSH by placing a text file in the boot folder of the SD card, similar to the wpa_supplicant trick in the previous section. For this trick, you just need to create an empty text file called ssh in the boot folder. This has worked for me in the past, when the RPi Imager OS customization step seemingly failed.
If you're able to connect to your RPi, that's awesome! But you might still want to make sure it's secure, and using password authentication for SSH is not the most secure option. If someone malicious ever gets onto your home network, or if you ever open up your RPi to the whole internet (as described in the next section), then it might be vulnerable to a brute force attack, in which an attacker repeatedly tries guessing your username and password. Public key authentication much more secure.
First of all, you will need a public-private key pair on your PC. OpenSSH stores them in a hidden directory called .ssh in your home directory. If you already have a key pair for your PC, you can skip this part. Otherwise, you can use OpenSSH to generate a public-private key pair for your user by running ssh-keygen. Your public key should be in a file called id_rsa.pub or similar, and your private key should be in a file with the same name but lacking the .pub extension, e.g. id_rsa. The private key is meant to be private - do not copy it anywhere!
Now connect to your user on the RPi using SSH (with password authentication, for now). Run ssh-keygen as your user. This will generate a public-private key pair for the user on the RPi. Run nano ~/.ssh/authorized_keys to create and open the authorized_keys file in your new user's SSH directory, and then paste your PC's public key into this file and save it. This will allow your PC to connect to the RPi as this user. The RPi will identify your PC by its public key, but the private key is how your PC will "prove" to the RPi that it is the legitimate owner of that public key. (Read more about how this works here!)
Now run sudo nano /etc/ssh/sshd_config to make edits to the RPi's SSH configutation. This is where we'll turn off password authentication entirely, and require that the more secure alternative of public key authentication is used. I suggest making sure the following settings are present in your /etc/ssh/sshd_config configuration file:
PermitRootLogin no
PubkeyAuthentication yes
PasswordAuthentication no
In the past, I've sometimes wanted to access my RPi from outside of my home network. You might want to do this if you've started a little coding project on your RPi that isn't available anywhere else, or if you want to check on some other resource that's only available from your home network, but you're out of the house at school, at work or at a coffee shop (as I often am). Naturally, you won't be able to SSH into pi.local anymore, because this hostname only exists on your private network. You won't be able to connect directly to the RPi by its IP address either, because private IP addresses are not globally unique.
If you're in this situation, a few options are available to you. One option is port forwarding together with dynamic DNS, but this is only viable if your home router has a public IP address, and if you actually have administrator privileges on your home router. Some internet service providers (ISPs) will give their customers a home router that don't have a public IP address accessible from the internet, or that can't be configured to set up port forwarding because customers aren't given admin privileges. Another possible avenue is to investigate software-defined networking tools like ZeroTier.
But in this section I'll describe another neat solution that has worked well for me before: SSH remote forwarding. In remote forwarding, a resource on a private network that is not exposed to the internet (in this case, the RPi) keeps a persistent connection with a remote server that is exposed to the internet. Then, when the remote server receives an SSH connection request to a certain port (say, from me, sitting in a coffee shop), it forwards this request to the private resource over the preexisting connection. You could picture it like this:
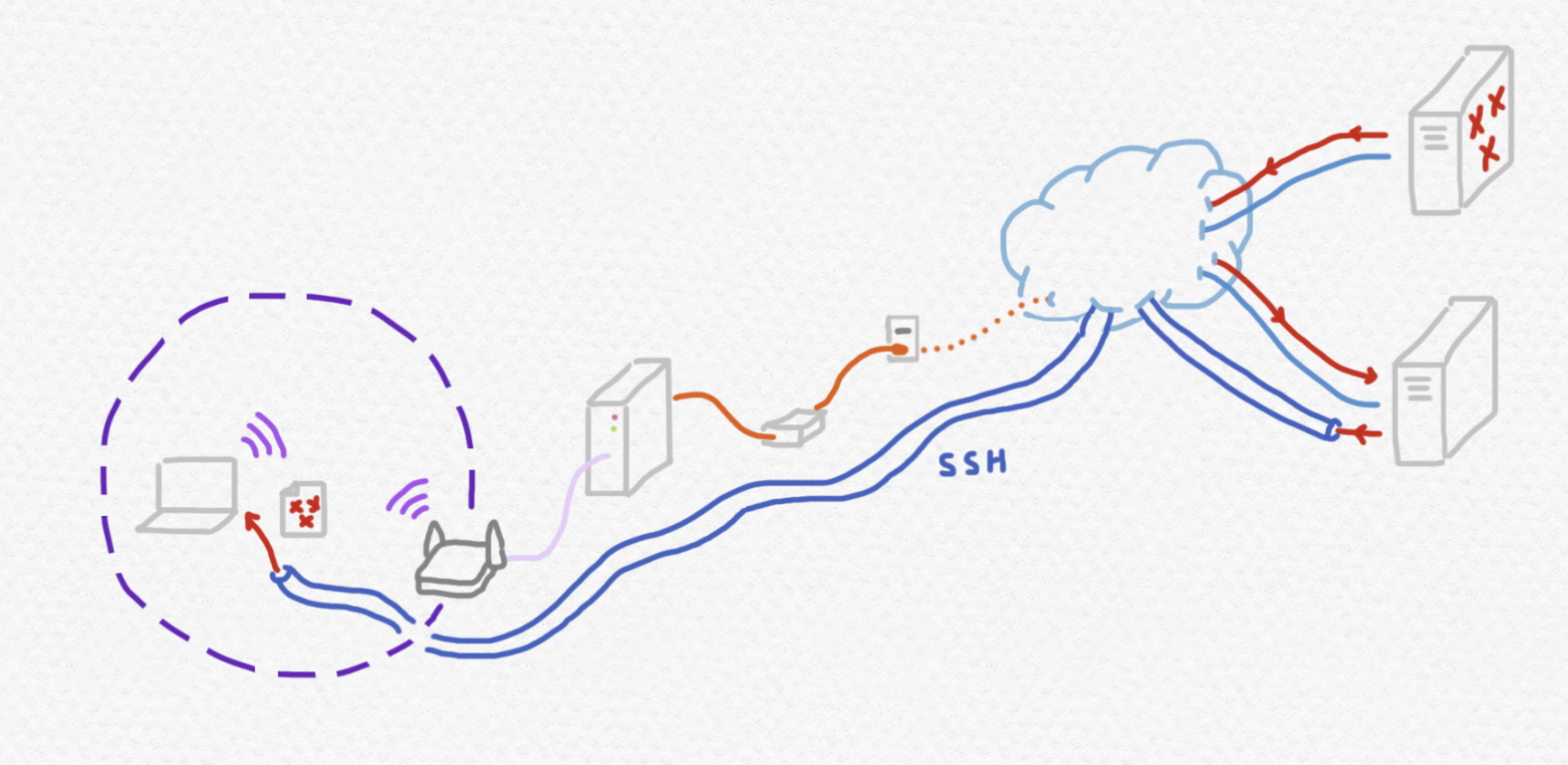
To implement this, you need a server with a public IP address that you can also access through SSH. I've had a good experience renting servers through DigitalOcean, or you can rent one through AWS.
When you have this, make sure SSH is installed on your public server, and make sure that a public-private keypair has been generated for your user on that server. Because we'll need the RPi to initiate an SSH connection to the remote server, we will need to add the public key for galois to the ~/.ssh/authorized_keys file for the new user on the remote server.
Next, you should install autossh on your RPi by running sudo apt-get install autossh. This is a tool that restarts SSH connections when they crash, which is essential when you want to have a long-lived connection like the kind that is necessary for remote port forwarding.
Let's say your user on the remote server is called chevalier, and the IP address of your remote server is W.X.Y.Z. From the Raspberry Pi, while logged in as the galois user, run the command autossh -R 2201:localhost:22 [email protected]. This will initiate the SSH remote port forward, with SSH requests directed at port 2201 of the remote server being forwarded to the RPi. Now, anywhere that your PC is connected to the internet, you should be able to run ssh -p 2201 [email protected] and connect to galois on your Raspberry Pi!
If this isn't working, you might want to check that port 2201 (or whatever port you chose) isn't being blocked by the firewall on your remote server, and that the configuration AllowTcpForwarding yes is set in the SSH config of the remote server. And if you're not sure how to make sure the autossh connection keeps running even after you log off of the RPi, check out the tools GNU screen and tmux. They allow you to start up a shell and disconnect from it in such a way that any processes continue running and you can reconnect to the shell at a later time.
To sum up, I usually follow these steps from beginning to end to set up my remote port forward:
galois and ensure autossh and screen are installedW.X.Y.Z and user chevalierAllowTCPForwarding is enabled and port 2201 is unblocked on W.X.Y.Zgalois (locally) and chevalier (remotely) if they don't already existgalois' public key into chevalier's authorized_keys filegalois, run screen to open a new screengalois, run the command autossh -R 2201:localhost:22 [email protected]galois, press Ctrl-A Ctrl-D to disconnect from the screen and leave autossh runninggalois