Totalidad y la recursión no estándar en Idris

Sigo jugueteando con la teoría de tipos dependientes y demostraciones verificadas por ordenador aprendiendo el lenguaje que se llama Idris. Me encanta Agda, pero a estas alturas me agrada un poco más Idris por el equilibrio que encuentra entre la utilidad cotidiana y los usos más "académicos", o sea como asistente para pruebas matemáticas. Todavía me veo como novato en estos temas, así que en vez de debatir los méritos de Idris me pongo a tratar un problema interestante y específico que he resuelto hace poco. (Encontrarás todo el código que he escrito para esta entrada en este repo de Github.)

Idris dispone de una herramienta muy chula que se llama la verificación de totalidad. Se dice que una función es total si se puede garantizar que su evaluación terminará "eventualmente" no obstante de la entrada que se meta en ella. Como el problema de la parada no es computable, no se puede algorítmicamente decidir si una función arbitraria entrará en un bucle infinito o no. Sin embargo, sí se puede confirmar que ciertos tipos de definiciones recursivas que cumplen con ciertos patrones definen funciones totales.

Por ejemplo, se puede saber por lo general que el siguiente tipo de definición es total:

f : Nat -> a
f 0     = x
f (S n) = g (f n)

en la que x : a es el valor de f en el caso base y g : a -> a es una función que se aplique iterativamente al caso base x. A los comprobadores de totalidad les gusta este tipo de definición porque el argumento a la función disminuye por uno en cada llamada recursiva. Si se puede ver que una de tus definiciones cumple con este esquema al llevar a cabo un análisis estático del código entonces el comprobador de totalidad le dará su visto bueno, pues es una manera conocida de definir funciones totales en Nat.

La totalidad es esencial en cuanto a escribir demostraciones. Si se permitiera que las demostraciones sean no totales, ¡entonces se podría demostrar cualquier cosa! En Idris (y Agda) se representa "la proposición falsa" como el tipo vacío, o sea Void en Idris. Si se permite demostraciones no totales, entonces se puede escribir la siguiente demostración de "falso", o sea, construir el siguiente elemento de Void:

x : Void
x = x

Claro, es una tontería. Si alguien te pide una demostración del enunciado $P$, entonces esto equivaldría a decir "pues claro! pídemelo mañana y te la daré". Y luego decir lo mismo el día siguiente, y etcétera. Si uno quiere usar un lenguaje para la verificación de demostraciones entonces claramente no debe permitir este tipo de fallo.

En Agda no sucede porque Agda es un lenguaje total, es decir que ni siquiera te permite escribir definiciones que no logra verificar como total. Bueno, pero una consecuencia un poco inconveniente de este hecho es que algunas funciones no se puede escribir en Agda, o sea, el lenguaje no es Turing completo. Además, la tarea de escribir ciertas funciones recursivas que sí son totales se vuelve más compleja porque la manera más obvia de escribirlas no cumple con los patrones esperados por el comprobador de totalidad de Agda. Idris hace un compromiso: no requiere que todas las funciones sean totales, pero puedes marcar funciones específicas con la palabra clave total si quieres que compruebe su totalidad en particular. Cualquiera demostración que escribas en Idris debe ser marcada como total.

Como ejemplo concreto consideramos la función recursiva $L:\mathbb N\to\mathbb N$ descrita por el caso base $L(0)=0$ y la fórmula recursiva siguiente: $$L(n) = 1 + L\big(\lfloor n/2\rfloor\big)$$ A propósito, los valores devueltos por esta función son explícitamente descritos por la fórmula siguiente cuando el argumento $n$ es positiva: $$L(n) = 1 + \lfloor \log_2 n \rfloor$$ En Idris se puede definir esta función directamente a través de su definición recursiva, así:

log2Careless : Nat -> Nat
log2Careless 0      = 0
log2Careless (S x)  = 1 + log2Careless (div2 $ S x)

en el cual bloque div2 es una función auxiliar que escribí para calcular la cantidad $\lfloor n/2\rfloor$. Esta definición funciona bien en Idris pero si intentas escribir una definición análoga en Agda entonces rechazará tu definición por no ser una que reconoce como total. Esto se debe a que su totalidad depende de las propiedades de la función div2 que está involucrada en la llamada recursiva. A fin de cuentas, si div2 fuera, digamos, la función de identidad en vez de $n\mapsto \lfloor n/2\rfloor$ entonces la misma definición produciría una función no total. De la misma manera si intentas marcar esta definición con la palabra total en Idris entonces se quejará, y bueno, esta queja sería bien justificada.

Pues naturalmente queremos poder tener las dos cosas a la vez. ¿Cómo escribir una función que cumple esta recurrencia y también es una función total? Al fin y al cabo, si queremos hacer mates puras en Idris tendremos que usar funciones totales.

Pues ¿te acuerdas de la función exemplar del principio, que es aceptada por el comprobador de totalidad por reducir su argumento por uno con cada llamada recursiva? Podemos emular este patrón agregando un segundo argumento que se comporta como un acumulador reduciéndose por uno con cada llamada. La nueva definición se ve así:

Claro que esto es una manera mucho menos directo de definir la misma función recursiva y ni es obvia que cumpla la misma recurrencia. Prefiero conceptualizar la diferencia entre estas dos definiciones gráficamente: podrías visualizar la sucesión de llamadas recursivas involucradas en la computación de $L(7)$ así para la definción "descuidada":

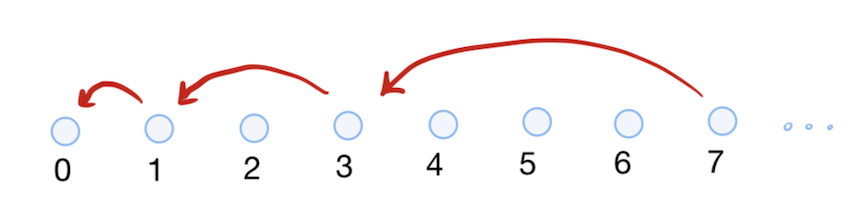
y así para la sucesión de llamadas recursivas involucradas en la computación de $L(7)$ para la definición "cuidadosa":

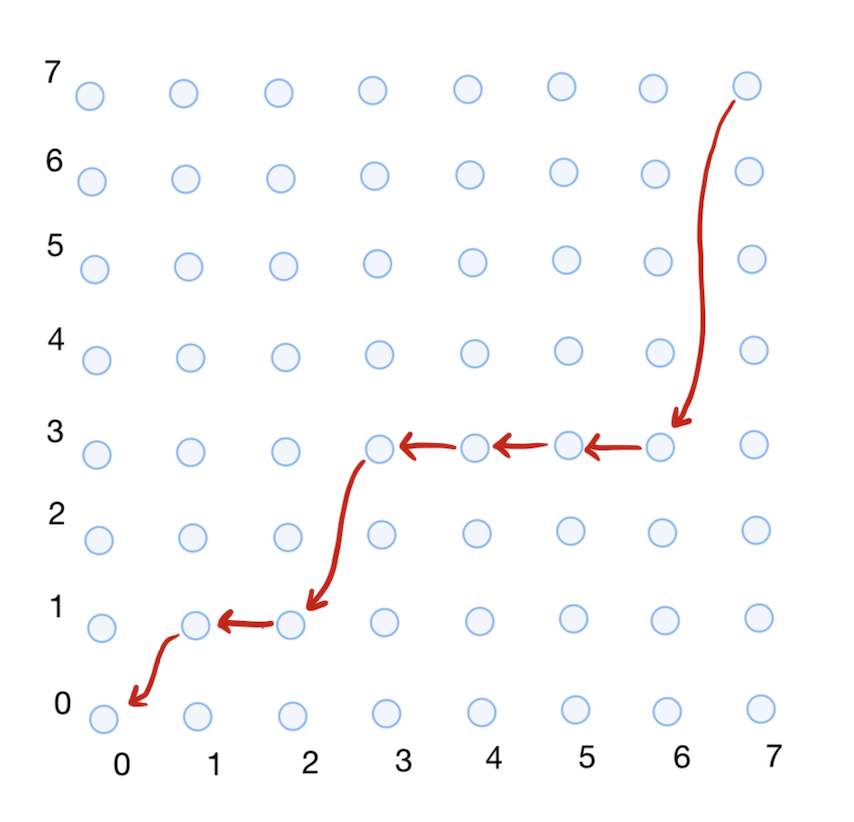
Si no nos viene obvio que esta función cumpla la misma recurrencia como $L$ entonces queda claro que ni se le saldrá obvio a Idris. Esto es lo que pagamos en cambio de la totalidad: la fórmula recursiva deja de ser parte de la definición, así que hace falta escribir una demostración para convencerle a Idris que log2Careful cumple la recurrencia de $L$ si aún queremos disponer de este hecho. La recurrencia se puede demostrar trivialmente para log2Careless como forma parte de su definición:

log2CarelessRecurrence : (n : Nat) ->
                         log2Careless (S n) = 1 + log2Careless (div2 $ S n)
log2CarelessRecurrence n = Refl

Pero si intentas marcar esta prueba como total entonces Idris se quejará que log2Careless no es total. Y pues una demostración que no sea total tiene muy poco valor, como hemos observado. Así que, aunque la definición de log2Careless es muy natural, no se porta bien en cuanto a las demostraciones.

Entonces lo que queremos es una demostración del tipo siguiente:

log2CautiousRecurrence : (n : Nat) ->
                         log2Cautious (S n) = 1 + log2Cautious (div2 $ S n)

No miento, esta demostración me fue un coñazo y me hizo falta bastante experiencia con los asistentes de pruebas antes de lograrlo por primera vez. Mi primer paso fue una proposición intermedia que se trató de la función log2CarefulHelper que asevera que cuando el segundo argumento supera el valor del primer argumento entonces se lo puede bajar hasta el valor del primer argumento sin afectar la salida de la función. Se puede observar este fenómeno en el diagrama que dibujamos para retratar las llamadas recursivas a log2Careful también. Está reflejado a través del hecho de que las flechas siempre apuntan horizontalmente y a la izquiertda hasta llegar al diagonal.

Pues aquí está mi demostración de este lema:

Demostrado ya este lema, el resto de la demostración no es tan dura. Aquí está:

Me ha costado mucho escribir estas demostraciones para una recurrencia tan sencilla, así que naturalmente quería escribirlo de una forma más abstracta para no tener que repetir toda la tarea de nuevo al escribir nuevas recurrencias sino simplemente utilizar mi implementación generalizada. Mi "plantilla de recurrencia" es bastante parecida a la función de orden superior foldr con unas pocas diferencias.

Primero, exige que el dominio a tenga alguna "función de tamaño" que le asigna a cada elemento de a un número natural que represente su "tamaño". Esto es preciso para captar la idea de una recurrencia "bien fundada". Para asegurar que una recurrencia en un dominio arbitrario termine, hay que poder expresar que realice llamadas recursivas en valores de entrada "más pequeños". Y pues esto presupone algún concepto de tamaño en los elementos de a.

Segundo, permite que la función recursiva tenga varios casos base. En concreto, los casos base se definen como los elementos de a con tamaño igual a cero. Podría existir varios elementos tales y son los preimagenes de 0 : Nat con respecto a la función size.

Tal y como hemos visualizado las llamadas recursivas de la función log2 anteriormente, podríamos visualizar la sucesión de llamadas recursivas involucrada en este tipo de recurrencia generalizada así:

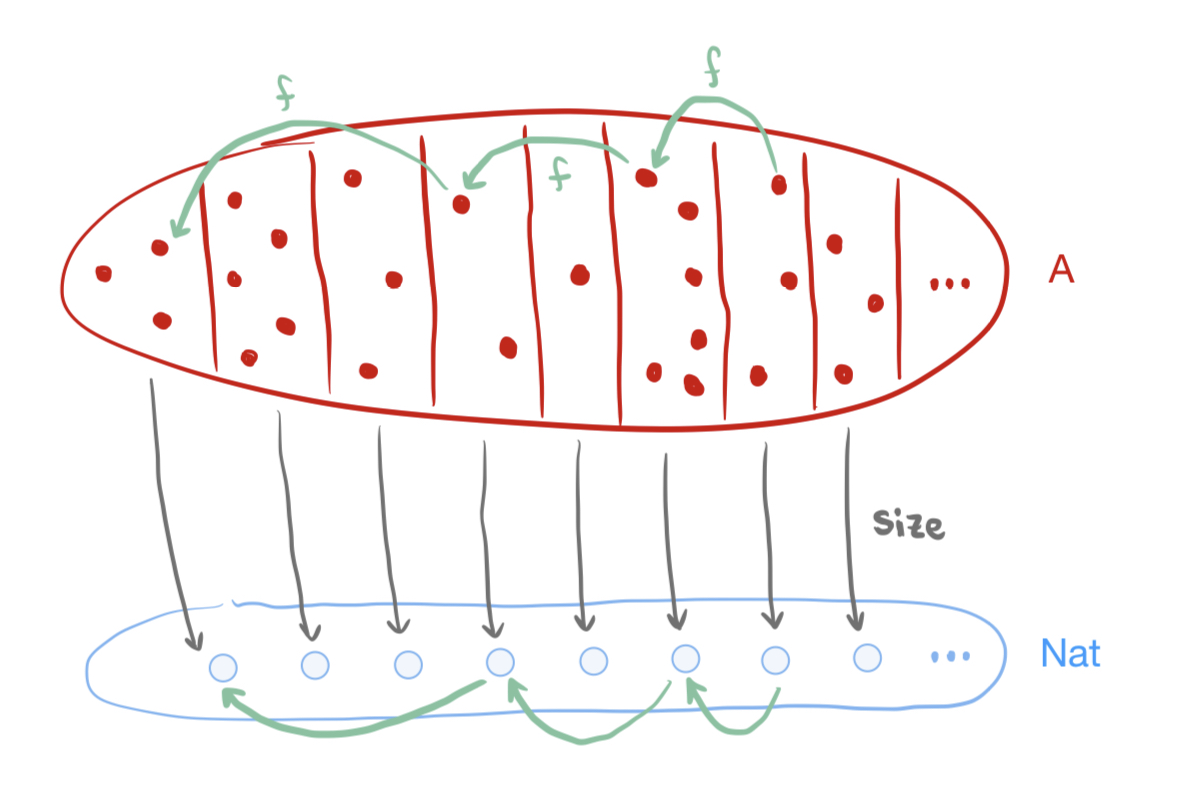
Para describir completamente una recurrencia que define una función recursiva a -> b, necesitamos una función recg : a -> b -> b que es homólogo de la función que se le pasa como argumento a foldr; una función recf : a -> a que le asigna a cada elemento de a un "caso previo"; una función size : a -> Nat que le asigna a cada elemento de a un tamaño; y una función base : a -> b que le asigna a cada entrada de tamaño cero un valor para el caso base correspondiente. Yo elegí una "clase de registro" (record type) en Idris para compilar todos estos datos:

public export
record GenericRecurrence a b where
    constructor MakeGenRec
    size : a -> Nat
    base : a -> b
    recf : a -> a
    recg : a -> b -> b 

Asi se puede implementar una función recursiva "descuidada" a partir de estos datos:

public export
carelessNatRecurse : GenericRecurrence a b -> (a -> b)
carelessNatRecurse gr x
    = if (gr.size x) == 0 
      then gr.base x 
      else gr.recg x (carelessNatRecurse gr (gr.recf x))

¡Esta se parece mucho a la definición de foldr! Pero desafortunadamente, como era el caso para nuestra función log2Careless, Idris no la reconoce como una función total (con razón, pues podría no ser total según la función recf que se use). Así que, aquí está mi implementación "cautelosa" de la misma función, que Idris sí reconoce como una función total:

total
cautiousHelper : GenericRecurrence a b -> (a -> Nat -> Nat -> b)
cautiousHelper gr x s 0 = gr.base x
cautiousHelper gr x s (S k)
    = caseSplit
        (\_ => gr.recg x (cautiousHelper gr (gr.recf x) (gr.size $ gr.recf x) k))
        (\_ => cautiousHelper gr x s k)
        (decLeq (S k) s)

total
public export
cautiousNatRecurse : GenericRecurrence a b -> (a -> b)
cautiousNatRecurse gr x = cautiousHelper gr x (gr.size x) (gr.size x)

Como antes, Idris no puede verificar que las funciones recursivas que se define usando cautiousNatRecurse cumplan la recurrencia que deben cumplir, así que hace falta escribir una demostración de la recurrencia. Ésta es tan fea y tan parecida a la que ya escribí para log2Cautious que no la copiaré aquí. Sin embargo, hay una diferencia interesante en la signature que vale comentar. (Por si acaso te interesa, puedes ver el código fuente.) La signatura se ve así:

La diferencia es que hay que proveer como argumento adicional una prueba de la propiedad de acotamiento de la función recf que garantiza que disminuya el tamaño de la entrada con cada llamada. No hizo falta para log2CautiousRecurrence porque en ese caso trabajabamos con una recurrencia concreta en la que cada llamada recursiva reduce el tamaño de la entrada por un factor de dos. En ese caso ya había demostrado la propiedad de acotamiento de div2 como lema externo llamado div2Leq, pero en el caso más general se tendría que proporcionar un lema análogo como argumento.

Por fin, aquí está una definición completa de la función $L$ que utiliza mi esquema abstracto en vez de una demostración manual:

Muy chulo, ¿no?