I was writing some C++ code to do computations involving polynomials. For my own gratification, I wanted to write a function that would pretty-print polynomials to my terminal, given a vector of coefficients. Naturally, I thought I'd use the special Unicode characters ⁰¹²³⁴⁵⁶⁷⁸⁹ to make the exponents look good, because x⁵ looks a lot nicer than x^5. I started by writing a function for translating a digit between 0 and 9 into its Unicode superscript counterpart.
char digit_superscript(int d) {
// some stuff here...
}
But no, that won't work. Unicode characters encoded using UTF8 can actually occupy up to four bytes. A char can only hold one byte, so I had to return a string instead.
string digit_superscript(int d) {
// some stuff here...
}
The easy (and probably performant) way of doing this would be to list out all ten cases and return the corresponding Unicode character. But that would be really ugly and repetitive code, and I don't care about how efficiently my polynomials are printed. I remembered an old trick that has served me well when working with ASCII: to get the nth letter of the alphabet, you can start with 'a' and simply add $n$, because the letters a..z are consecutive. So perhaps I could get the superscript digit for $d$ by starting with the code point for ⁰ and adding $d$.
The character ⁰ is code point U+2070, which is encoded in UTF8 as the bytes e2 81 b0. So I gave this a try:
string digit_superscript(int d) {
string num = "\xe2\x81\xb0";
num.at(2) += d;
return num;
}
And I tested the function by trying to print out the digits from zero through nine:
int main() {
for (int i = 0; i < 10; i++)
cout << digit_superscript(i);
cout << "\n";
}
The output was ⁰ⁱ⁴⁵⁶⁷⁸⁹. What the fuck?
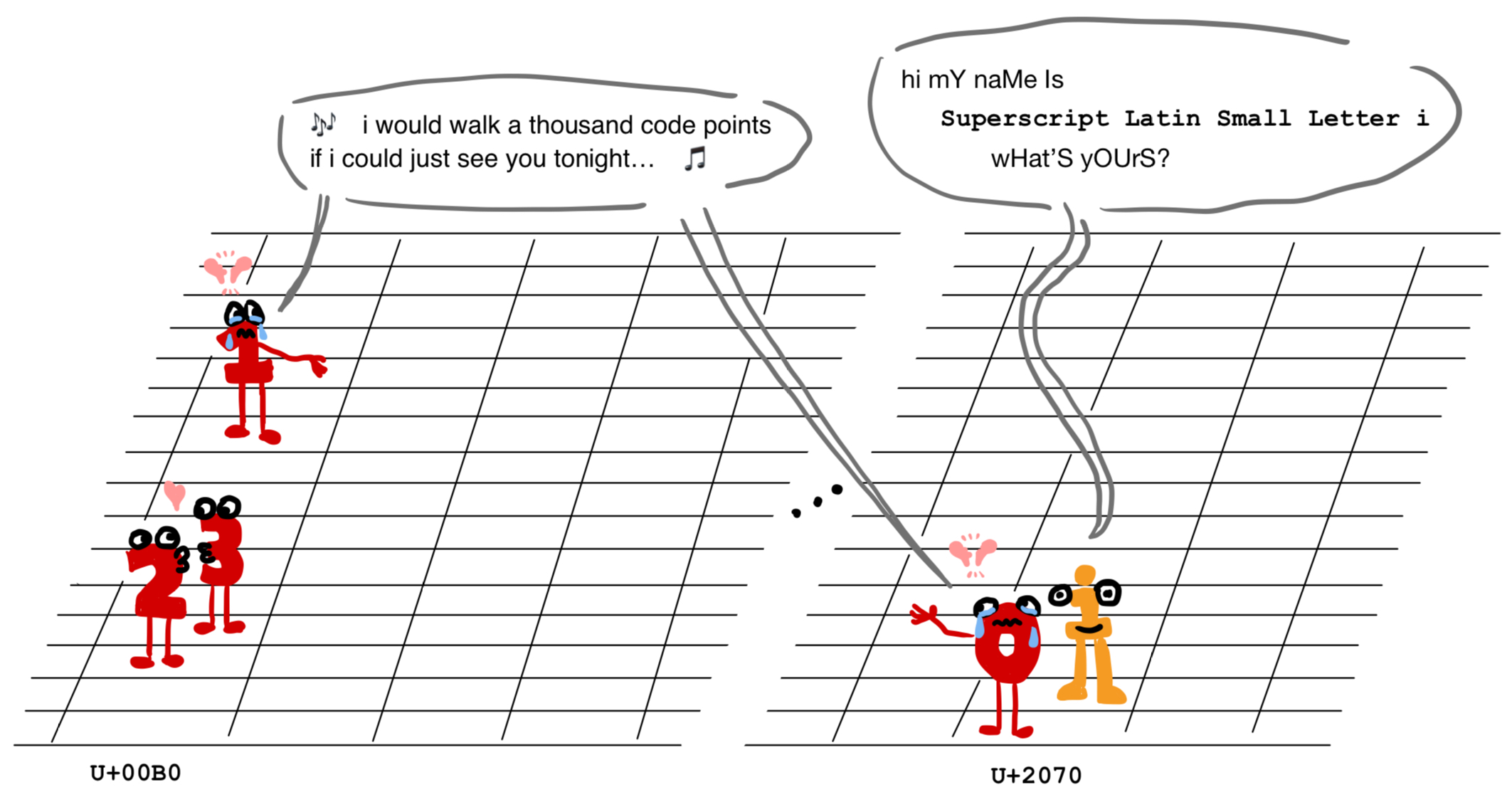
That's right: the Unicode superscript digits are not consecutive. The superscript zero is U+2070, but U+2071 is the superscript "i" character ⁱ. Even better, the code points U+2072 and U+2073 are not mapped to any character at all right now, just "reserved for future use". The superscript digits ⁴⁵⁶⁷⁸⁹, however, are fortunate enough to occupy the consecutive code points from U+2074 through U+2079.
So what's the deal with ¹²³? According to Wikipedia they are inherited from the encoding ISO-8859-1, which was a single-byte encoding extending ASCII that possessed these three superscript digits and none of the other seven. Unicode was considerate enough to allow the ISO-8859-1 characters to retain their code points in its Latin-1 block, with the unfortunate consequence that the superscript digits ¹²³ be separated from their bretheren by 8000 or so characters. But hey, at least ⁰ has ⁱ to keep it company. They're vaguely related, right? You know, because they're both superscripted... things?
Not only that, but ¹²³ were not even consecutive in ISO-8859-1. The characters ²³ are U+00B2 and U+00B3, but ¹ is U+00B9. Lovely.

Alright, back to coding. I was able to use the offset trick for the digits ⁰⁴⁵⁶⁷⁸⁹ but the digits ¹²³ have to be treated as their own special case.
string digit_superscript(int d) {
switch (d) {
case 1:
return "\u00b9";
case 2:
return "\u00b2";
case 3:
return "\u00b3";
default:
string num = "\xe2\x81\xb0";
num.at(2) += d;
return num;
}
}
How disgusting...