Skip to page content Home     Posts     CV     Contact     People

Interesting Trigonometric Integrals

2018 June 16

NOTE: I will use a special notation during this post that may be unfamiliar to some. The symbol $\delta_{ij}$, a function of $i$ and $j$, is defined as $1$ if $i=j$ and $0$ otherwise... pretty simple, but handy since it allows one to avoid piecewise notation.

NOTE: One more piece of helpful notation - the Iverson Bracket. If $A$ is some logical statement, then $[A]$ is equal to $1$ if $A$ is true and $0$ if $A$ is false. For example, $[2018\space\text{is odd}]=0$, and $\delta_{ij}=[i=j]$.

$$\int_0^\pi \frac{\cos(5x)}{5-\cos(x)}dx$$ $$\int_0^\pi \frac{dx}{(5-4\cos(x))(5-4\cos(2x))}$$ $$\int_0^\infty \frac{1-\cos(2x)}{5-4\cos(2x)}\frac{dx}{x^2}$$ $$\int_0^\infty \ln(2-2\cos(x^2))dx$$

WARNING: Don't try to calculate the last integral in any nice closed form - I calculated it in terms of a fractional value of the Zeta function.

As with my last blog post, the integrals provided as "warm-ups" are only specific cases of more useful generalizations that I will derive during this post. Interestingly, some of these integrals involve a bit of number theory, which we will discover shortly...

Let us begin with the following integral, which I have not included in the warm-ups, but which is crucial in my derivation of many of them: $$\int_0^\pi \cos(mx)\cos(nx)dx$$ ...where $m$ and $n$ are positive integers. Using the following trigonometric identity: $$\cos(\theta)\cos(\phi)=\frac{\cos(\theta+\phi)+\cos(\theta-\phi)}{2}$$ we can transform the integral into the following: $$\int_0^\pi \frac{\cos((m+n)x)+\cos((m-n)x)}{2}dx$$ which easily evaluates to $$\frac{\sin((m+n)\pi)}{2m+2n}+\frac{\sin((m-n)\pi)}{2m-2n}$$ which vanishes for any positive integers $m,n$, since the sine of an integer multiple of $\pi$ is zero. However, this integral isn't valid for $m=n$, because the second term, in that case, is indeterminant. When $m=n$, the integral becomes instead $$\int_0^\pi \frac{\cos((m+n)x)+\cos(0)}{2}dx$$ which evaluates to $\pi/2$. Thus, our original integral vanishes when $m\ne n$ and is equal to $\pi/2$ when $m=2$, giving us the following result: $$\int_0^\pi \cos(mx)\cos(nx)dx=\frac{\pi}{2}\delta_{mn}$$ ...a rather tame result on its own, but, in conjunction with some other trigonometric series and integral identities, it can lead to some fascinating ones.

To start us on this journey, I shall begin with a rather ordinary generating function identity. As we all know, $$\sum_{n=0}^\infty x^n=\frac{1}{1-x}$$ By replacing $x$ with $ze^{i\theta}$, we have the following: $$\begin{align} \sum_{n=0}^\infty (ze^{i\theta})^n &=\frac{1}{1-ze^{i\theta}}\\ &=\frac{1}{1-z\cos\theta-iz\sin\theta}\\ &=\frac{1-z\cos\theta+iz\sin\theta}{(1-z\cos\theta-iz\sin\theta)(1-z\cos\theta+iz\sin\theta)}\\ &=\frac{1-z\cos\theta+iz\sin\theta}{(1-z\cos\theta)^2+z^2\sin^2\theta}\\ &=\frac{1-z\cos\theta+iz\sin\theta}{1-2z\cos\theta+z^2\cos^2\theta+z^2\sin^2\theta}\\ &=\frac{1-z\cos\theta+iz\sin\theta}{1-2z\cos\theta+z^2}\\ \end{align}$$ By equating real and imaginary parts, this demonstrates that $$\sum_{n=0}^\infty z^n\cos(n\theta)=\frac{1-z\cos\theta}{1-2z\cos\theta+z^2}$$ $$\sum_{n=0}^\infty z^n\sin(n\theta)=\frac{z\sin\theta}{1-2z\cos\theta+z^2}$$

Now, let's consider what this means when applied to our integral. We know that $$\int_0^\pi \cos(mx)\cos(nx)dx=\frac{\pi}{2}\delta_{mn}$$ Thus if $k$ is a positive integer, then $$\int_0^\pi z^k\cos(mkx)\cos(nx)dx=\frac{\pi}{2}z^k\delta_{(mk)n}$$ By summing both sides from $k=0$ to $\infty$, we get the following: $$\int_0^\pi \frac{1-z\cos(mx)}{1+z^2-2z\cos(mx)}\cos(nx)dx=\frac{\pi}{2}z^{n/m}[m|n]$$ ...as long as $|z|<1$, to ensure convergence. By decomposing that ugly fraction in the integral, we get the following: $$\frac{1}{2}\int_0^\pi \bigg(\frac{1-z^2}{1+z^2-2z\cos(mx)}+1\bigg)\cos(nx)dx=\frac{\pi}{2}z^{n/m}[m|n]$$ ...and, recalling the assumption that $n$ is an integer, we have

$$\bbox[lightgray,5px]{ \int_0^\pi \frac{\cos(nx)}{1+z^2-2z\cos(mx)}dx=\frac{\pi z^{n/m}[m|n]}{1-z^2} }$$

This formula holds for $m,n\in\mathbb Z^+$ and $|z|<1$. Using it, we can easily resolve our first warm-up problem by setting $n=5$, $m=1$, and $z=5-2\sqrt{6}$:

$$\bbox[lightgray,5px]{ \int_0^\pi \frac{\cos(5x)}{5-\cos(x)}dx=\frac{2\pi (5-2\sqrt{6})^6}{1-(5-2\sqrt 6)^2} }$$

...but we can do even better! In fact, we can do yet another infinite series! Let's begin this time with the formula we just derived:

$$\int_0^\pi \frac{\cos(nx)}{1+z^2-2z\cos(mx)}dx=\frac{\pi z^{n/m}[m|n]}{1-z^2}$$

This time, we'll replace $n$ with $nk$, where $k$ is a positive integer. For convenience's sake, I'll also replace $z$ with $a$.

$$\int_0^\pi \frac{\cos(nkx)}{1+a^2-2a\cos(mx)}dx=\frac{\pi a^{nk/m}[m|nk]}{1-a^2}$$

Now multiply both sides by $b^k$, for some $b$ satisfying $|b|<1$:

$$\int_0^\pi \frac{b^k\cos(nkx)}{1+a^2-2a\cos(mx)}dx=b^k\frac{\pi a^{nk/m}[m|nk]}{1-a^2}$$

Finally (can you guess what to do now?) I will sum both sides from $k=0$ to $\infty$, resulting in

$$\int_0^\pi \frac{1}{1+a^2-2a\cos(mx)}\frac{1-b\cos(nx)}{1+b^2-2b\cos(nx)}dx=\sum_{k=0}^\infty b^k\frac{\pi a^{nk/m}[m|nk]}{1-a^2}$$

Now notice that $[m|nk]$ is equal to zero unless $k$ is a multiple of $m/\gcd(m,n)$, in which case it is equal to $1$. Thus, our series can be converted to

$$\sum_{k=0}^\infty b^{mk/\gcd(m,n)}\frac{\pi a^{nk/\gcd(m,n)}}{1-a^2}$$

which is just a geometric series, converging to

$$\frac{\pi}{(1-a^2)(1-a^{n/\gcd(m,n)}b^{m/\gcd(m,n)})}$$

and so we have

$$\int_0^\pi \frac{1}{1+a^2-2a\cos(mx)}\frac{1-b\cos(nx)}{1+b^2-2b\cos(nx)}dx=\frac{\pi}{(1-a^2)(1-a^{n/\gcd(m,n)}b^{m/\gcd(m,n)})}$$

using the same partial fraction decomposition as before, we end up with the following: $$\int_0^\pi \frac{1}{1+a^2-2a\cos(mx)}\frac{1}{1+b^2-2b\cos(nx)}dx=\frac{2\pi}{(1-a^2)(1-b^2)(1-a^{n/\gcd(m,n)}b^{m/\gcd(m,n)})}-\frac{\pi}{(1-a^2)(1-b^2)}$$ or $$\bbox[lightgray,5px]{ \int_0^\pi \frac{dx}{(1+a^2-2a\cos(mx))(1+b^2-2b\cos(nx))}=\pi\frac{1+a^{n/\gcd(m,n)}b^{m/\gcd(m,n)}}{(1-a^2)(1-b^2)(1-a^{n/\gcd(m,n)}b^{m/\gcd(m,n)})} }$$

Letting $m=1$, $n=2$, and $a=b=1/2$ gives the answer to the second warm-up:

$$\bbox[lightgray,5px]{ \int_0^\pi \frac{dx}{(5-4\cos(x))(5-4\cos(2x))}=\frac{\pi}{7} }$$

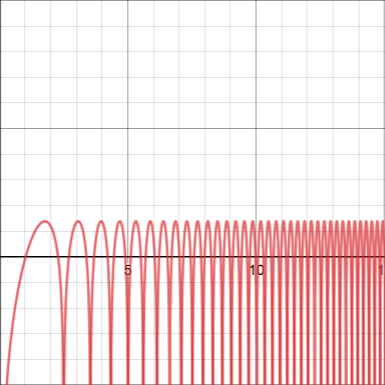
Now we will use the infinite series identity derived earlier to exploit an entirely different type of integral. Consider the well-known identity $$\int_0^\infty \frac{\sin(ax)}{x}dx=\frac{\pi}{2}$$ for any value of $a$. By antidifferentiating both sides with respect to $a$, we obtain the integral $$\int_0^\infty \frac{1-\cos(ax)}{x^2}dx=\frac{\pi a}{2}+C$$ where $C$ is some constant. By setting $a=0$, we see that $C=0$, and so $$\int_0^\infty \frac{1-\cos(ax)}{x^2}dx=\frac{\pi a}{2}$$ Then replace $a$ with $ak$ for some positive integer $k$, and multiply both sides by $z^k$, where $|z|\lt 1$. This gives us $$\int_0^\infty \frac{z^k-z^k\cos(axk)}{x^2}dx=\frac{\pi a}{2}\cdot kz^k$$ Now, as before, we sum both sides from $k=1$ to $\infinity$, and use this series identity before on the LHS: $$\sum_{n=0}^\infty z^n\cos(n\theta)=\frac{1-z\cos\theta}{1-2z\cos\theta+z^2}$$ and use the following well-known series identity on the RHS: $$\sum_{k=1}^\infty kz^k=\frac{z}{(1-z)^2}$$ This gives us the following equality: $$\int_0^\infty \bigg(\frac{1}{1-z}-\frac{1-z\cos(ax)}{1+z^2-2z\cos(ax)}\bigg)\frac{dx}{x^2}=\frac{\pi a}{2}\cdot \frac{z}{(1-z)^2}$$ $$\int_0^\infty \frac{z^2+z-(z^2+z)\cos(ax)}{1+z^2-2z\cos(ax)}\frac{dx}{x^2}=\frac{\pi a}{2}\cdot \frac{z}{(1-z)^2}$$ or, as our final result, $$\bbox[lightgray,5px]{ \int_0^\infty \frac{1-\cos(ax)}{1+z^2-2z\cos(ax)}\frac{dx}{x^2}=\frac{\pi a}{2}\cdot \frac{1}{(1-z)^2(1+z)} }$$ Plugging in $z=1/4$, we get the value of our third warm-up problem: $$\bbox[lightgray,5px]{ \int_0^\infty \frac{1-\cos(2x)}{5-4\cos(2x)}\frac{dx}{x^2}=\frac{\pi}{3} }$$ For the next warm-up integral, before I start to solve it, I'd like to show a picture of its graph. It is, of course, an improper integral, but over the interval $(0,\infty)$, not only does its integrand contain infinitely many singularities, but they occur more and more frequently, making it very improper (so improper that Wolfram Alpha can't even approximate it effectively), but still convergent.

To quickly derive the value of this integral, one can employ the integral identity $$\int_0^\infty \cos(ax^2)dx=\frac{1}{2}\sqrt{\frac{\pi}{2a}}$$ and the well-known Fourier series $$\sum_{k=1}^\infty \frac{\cos(kx)}{k}=-\frac{\ln(2-2\cos(x))}{2}$$ By replacing $a$ with $ak$ in the first integral and dividing both sides by $k$, one obtains $$\int_0^\infty \frac{\cos(akx^2)}{k}dx=\frac{1}{2}\sqrt{\frac{\pi}{2a}}\frac{1}{k^{3/2}}$$ Then, summing from $k=1$ to $\infty$, one gets $$\bbox[lightgray,5px]{ \int_0^\infty \ln(2-2\cos(ax^2))dx=-\sqrt{\frac{\pi}{2a}}\zeta(3/2) }$$ By plugging in $a=1$, one gets the value of the fourth and final warm-up: $$\bbox[lightgray,5px]{ \int_0^\infty \ln(2-2\cos(x^2))dx=-\sqrt{\frac{\pi}{2}}\zeta(3/2) }$$ Now, before ending this blog post, I would like to show off an integral that I derived using trigonometric series. Using the Fourier Series that we employed for the previous series, and using the identity $$\int_0^\pi \cos(mx)\cos(nx)dx=\frac{\pi}{2}\delta_{mn}$$ from earlier,along with various trigonometric identities, I managed to prove the following awesome identity for $m,n\in\mathbb Z$: $$\bbox[lightgray,5px]{ \int_0^{\pi/2}\ln|\sin(mx)|\ln|\sin(nx)|dx=\frac{\pi^3}{24}\frac{\gcd^2(m,n)}{mn}+\frac{\pi\ln^2(2)}{2} }$$

If you want, you can try it as well. And, to finish off the post, I propose the following exercise: see what integrals you can derive using trigonometric series and the following identity, derived in my post on the Residue Theorem:

$$\int_{-\infty}^\infty \frac{\cos(ax)}{x^2+1}dx=\pi e^{-|a|}$$