Skip to page content Home     Posts     CV     Contact     People

Area Under a Sine Arch

2017 Mar 9

I noticed something funny the other day.

Consider a sine graph with equation $y=c*\sin(cx)$, where $c$ is a constant. The period of such a sine wave is $\frac{2\pi}{c}$, so the area under a single one of its arches is $$A=\int_0^{\frac{\pi}{c}} c\sin cx \,dx$$

Which is $$A=-\cos \pi + \cos 0$$ $$A=2$$

That struck me as a little odd. Regardless of the value of $c$, the area underneath a single arch was always $2$? But I suppose it makes sense, because as $c$ increases, each arch is stretched vertically but compressed horizontally. However, it gets weirder. If $y=f'(x)\sin f(x)$, the area is still $2$, because the x-coordinates of the start and endpoints of the nth arch are $f^{-1}(\pi n-\pi)$ and $f^{-1}(\pi n)$ for integral $n$, the area under the nth arch is $$A=\int_{f^{-1}(\pi n-\pi)}^{f^{-1}(\pi n)} c\sin cx \,dx$$

Which simplifies to $$-\cos f(f^{-1}(\pi n))+\cos f(f^{-1}(\pi n-\pi))$$ $$-\cos \pi n+\cos (\pi n-\pi)$$

We are interested in only positive areas, and the positive difference between $-\cos \pi n$ and $\cos (\pi n-\pi)$ is the difference between two consecutive peaks of the cosine arch, which is also always $2$.

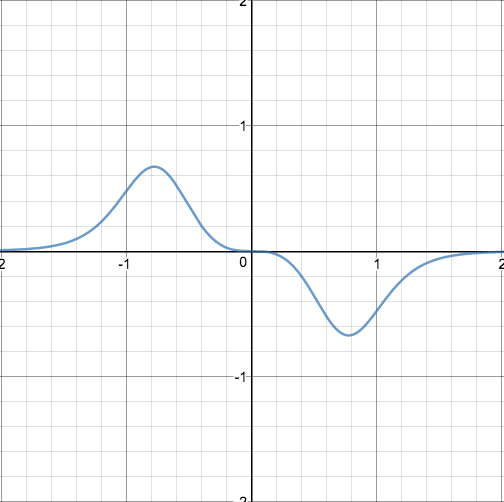
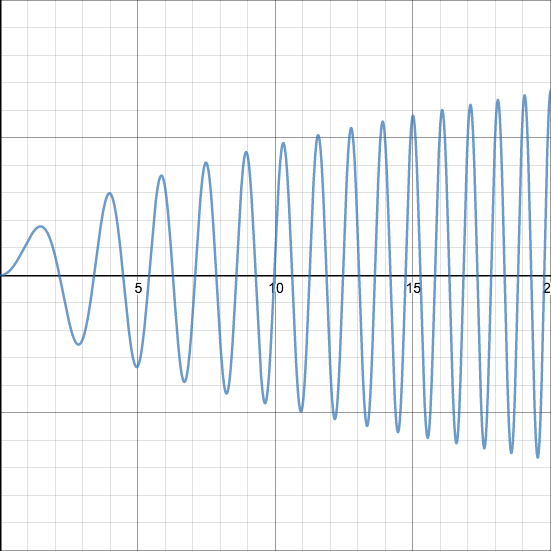
That means that all of the areas underneath all of the arches in the following pictures is equal to $2$: