Do not use a calculator for any of these problems. Don't Google them, either.
Do your best to solve them, but if you get stuck and can't find an answer to all parts of a problem, don't worry. We can talk about it together, and you can always come back and try to solve it again later.
Problem 1. In the set of rational numbers, sometimes written $\mathbb Q$, we say that two numbers are reciprocals or inverses of each other if they multiply to $1$. For example, $1/3$ is a reciprocal of $3$ because $3\cdot (1/3) = 1$. Not all of the numbers in $\mathbb Q$ have reciprocals - for example, $0\in\mathbb Q$ does not have any inverse.
By now we have talked about the different "clock-like" number systems $\mathbb Z_m$, sometimes called "the integers modulo $m$". Spend some time studying reciprocals in different moduli. For example:
Do you notice any patterns? Do you have any conjectures about when a number $a\in\mathbb Z_m$ has a reciprocal or not?
Problem 2. Perform polynomial division to calculate $(1 + x)^{10} \bmod (x^2 - 2)$. Also perform polynomial division to calculate $(1-x)^{10}\bmod (x^2 - 2)$. Do you notice anything interesting? Is this similar to any other calculations you've done recently?
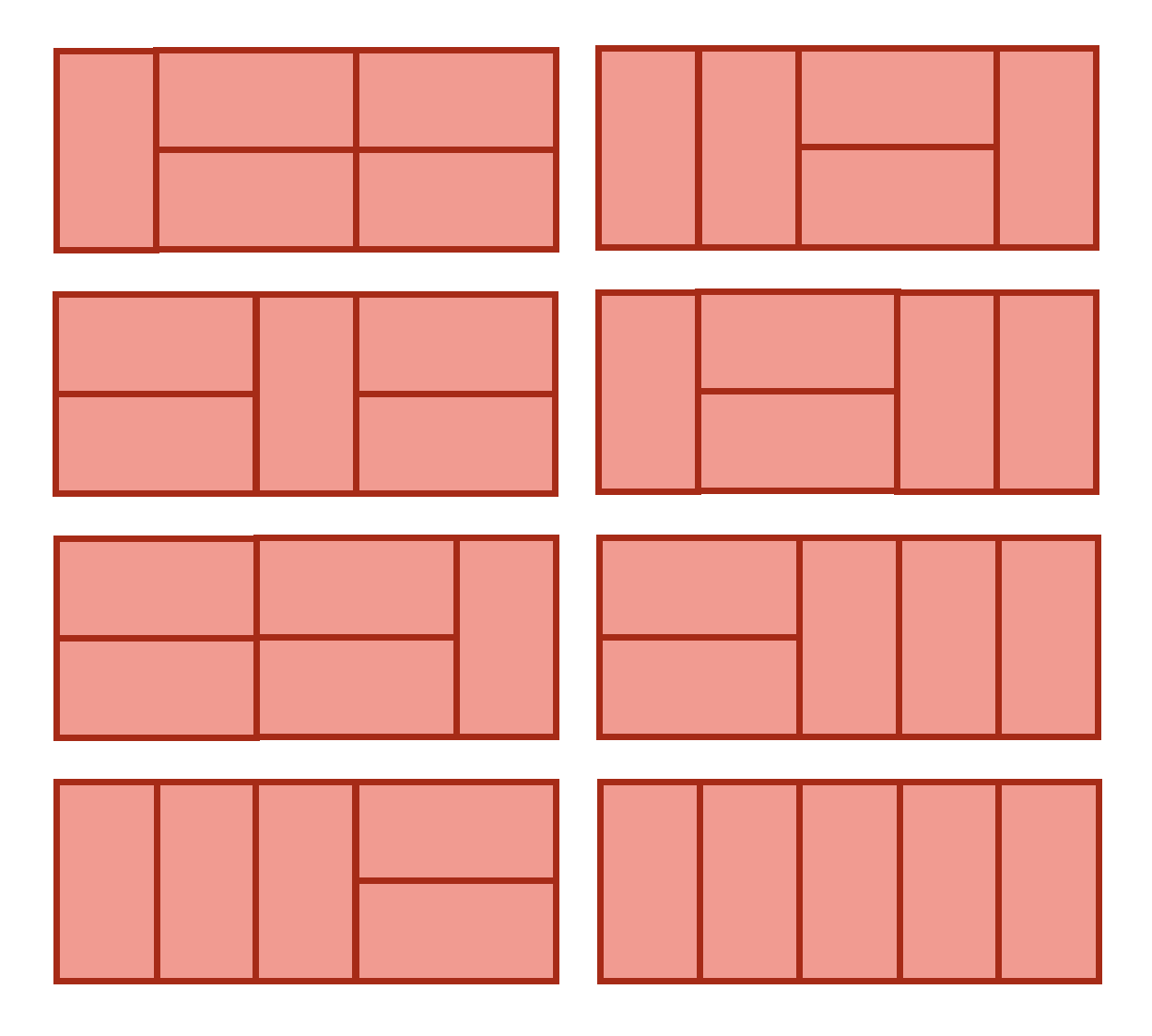
Problem 3. Investigate how many ways there are to cover an $n\times 2$ rectangle with non-overlapping $2\times 1$ dominos. For example, when $n=5$, there are the following $8$ ways:

How many ways are there for $n=1,2,3,4,6,7$? Can you find a general formula or pattern that can be used to count the number of ways for any $n$? How many ways are there for a $20\times 2$ rectangle?