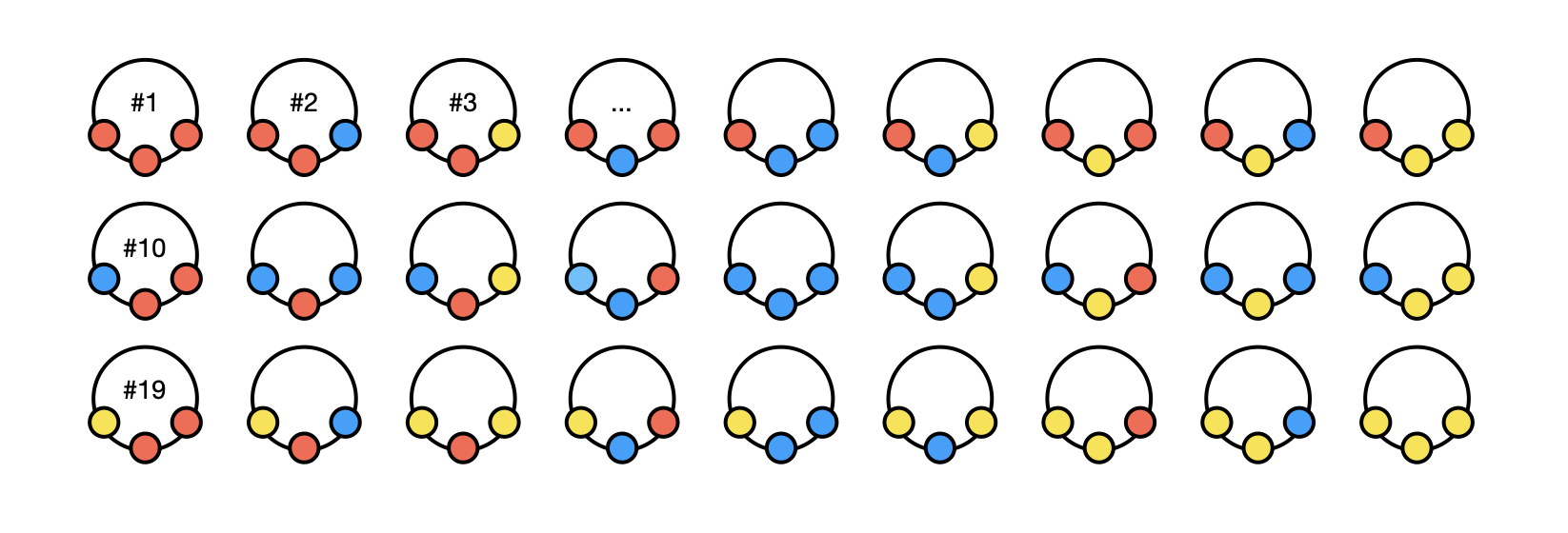
Do not use a calculator for any of these problems. Don't Google them, either.
Do your best to solve them, but if you get stuck and can't find an answer to all parts of a problem, don't worry. We can talk about it together, and you can always come back and try to solve it again later.
Problem 1. Investigate the powers of $2$ in $\mathbb Z_{29}$. Calculate $2^1,2^2,\cdots, 2^{30}$ modulo $29$. Calculate $2^{100}$ and $2^{200}$ modulo $29$. Do you notice anything interesting?
Next, make a table of the reciprocals of all of the numbers in $\mathbb Z_{29}$ (that have reciprocals). (This is not completely unrelated to the first part of this problem. You've done a lot of tedious calculation in the first part of the problem - can you use it to make your work easier for this part?)
Problem 2. The numbers $a_n$ are defined like this: Calculate $a_1$ through $a_{10}$ in simplest form as fractions $p/q$. Do you notice any pattern in these values? Does the sequence $a_1,a_2,a_3,\cdots$ have a limit? If so, what is its limit?
Problem 3. Suppose you are making necklaces with colored beads, and there are $3$ different colors (red, blue, yellow). If you use $3$ beads on a necklace, at first glance, there are $3^3 = 27$ different necklaces you could make, since there are $3$ color choices for each bead:
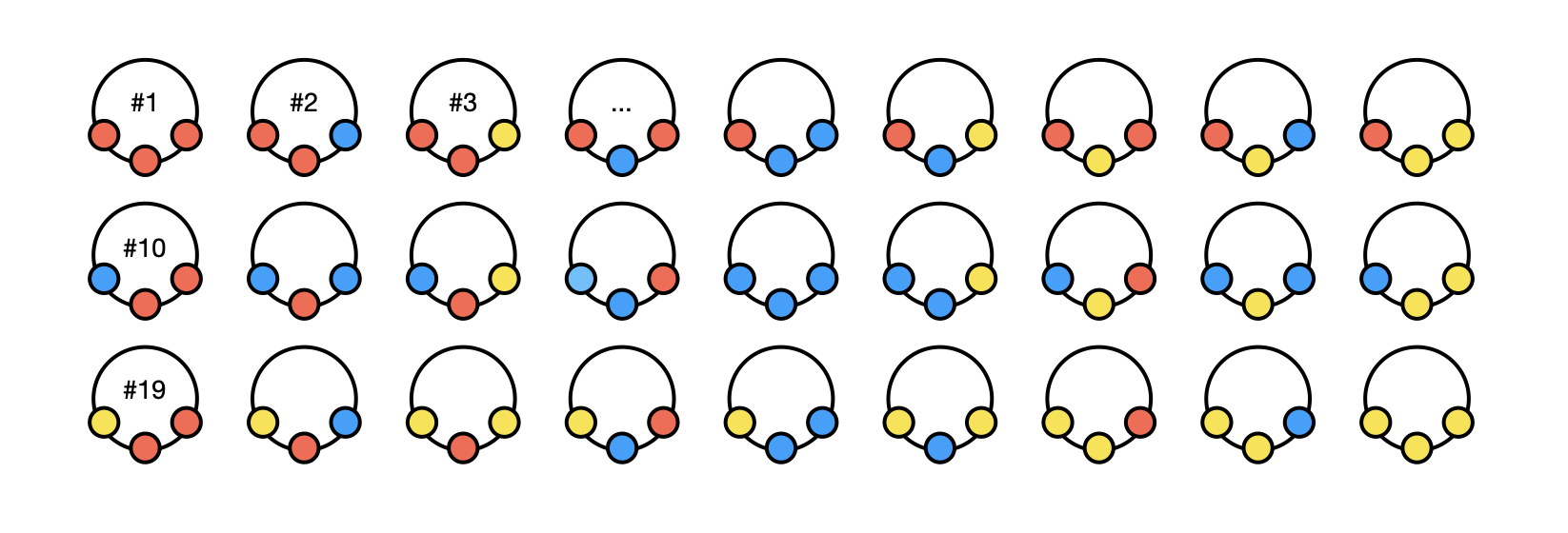
However, these necklaces are not actually all different from each other. For example, necklace 2 and necklace 10 are actually the same necklace - the blue bead is just pushed around the back to the other side. Similarly, both 2 and 10 are also the same as necklace 4.
So, how many different necklaces with 3 colors and 3 beads are there actually? How about with $4$ colors and $3$ beads? How about a general formula $n$ colors and $3$ beads?
Try to consider the cases with different numbers of beads as well. Are things any different if you try to count the number of necklaces with $4$ beads? $5$ beads? Can you come up with general formulas for te number of different necklaces with $4$ beads (or $5$ beads, or $6$ beads) if there are $n$ different colors of beads?