Derivation of the Weierstrass elliptic integral periods

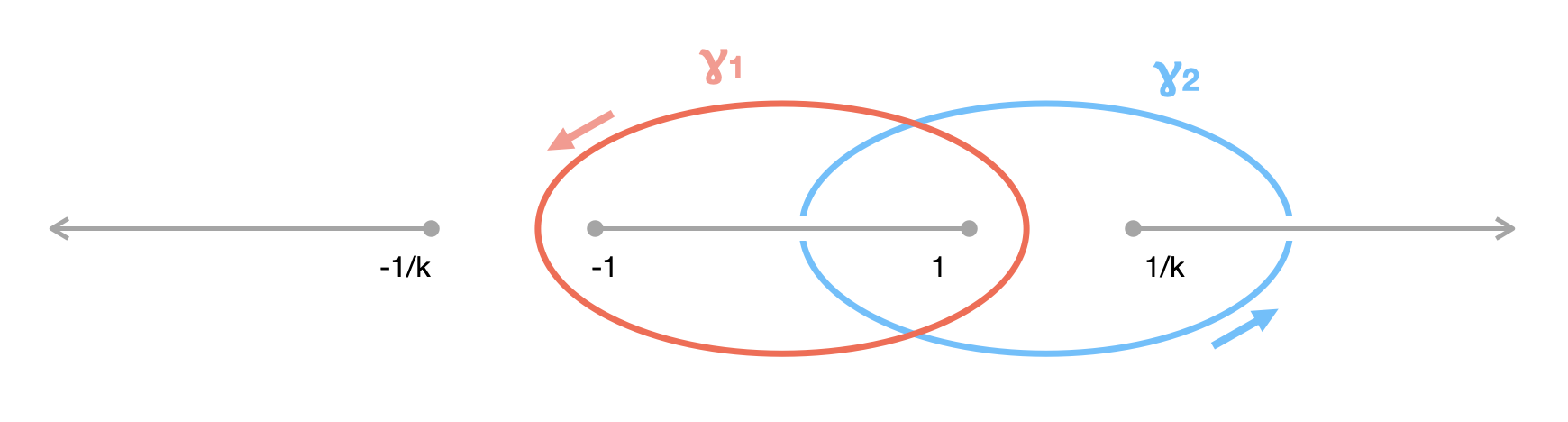
The two periods $\omega_1,\omega_2$ are given by the following two contour integrals: $$\begin{align*}\omega_1 &= \int_{\gamma_1} \frac{dz}{\sqrt{(1-z^2)(1-k^2 z^2)}} \\ \omega_2 &= \int_{\gamma_2} \frac{dz}{\sqrt{(1-z^2)(1-k^2 z^2)}}\end{align*}$$

By contracting the contour $\gamma_1$ infinitesimally tightly around the branch cut $[-1,1]$, and noticing that there is a sign reversal as $z$ traverses the path from a point on the upper side of the cut to the corresponding point on the lower side of the cut, we find that $$\omega_1 = -2\int_{-1}^1 \frac{dz}{\sqrt{(1-z^2)(1-k^2 z^2)}} = -4\int_0^1 \frac{dz}{\sqrt{(1-z^2)(1-k^2z^2)}} = -4K(k)$$ Similarly, as we contract $\gamma_2$ around $[1,k^{-1}]$, there is a sign change as the upper and lower sides of the path lie on opposite leaves of the Riemann surface, so that rather than cancelling each other, their values are doubled. We have: $$\omega_2 = 2i\int_1^{1/k} \frac{dz}{\sqrt{(z^2-1)(1-k^2 z^2)}}$$ Next, to express this in terms of the complete elliptic integral of the first kind, we perform the following substitution: $$z = \frac{1}{\sqrt{1-k'^2 w^2}}$$ so that $$dz = \frac{k'^2 w ~ dw}{(1-k'^2 w^2)^{3/2}}$$ and, after simplification, $$\omega_2 = 2i\int_0^1 \frac{dw}{\sqrt{(1-w^2)(1-k'^2 w^2)}} = 2iK(k')$$ Which gives our final expressions for the elliptic periods: $$\begin{align*}\omega_1 &= -4K \\ \omega_2 &= 2iK'\end{align*}$$