Skip to page content Home     Posts     CV     Contact     People

Tilted Parabola

2016 Dec 7

Find the equation of the graph of a parabola that is neither vertical or horizontal.

It is commonly known that a parabola is the locus of all points equidistant from a point, called the focus, and a line, called the directrix. The quadratic function represents a parabola with a horizontal directrix, and the square root function can represent half of a parabola with a vertical directrix. Given a horizontal or vertical directrix, it is easy to write the equation of the parabola, since the distance of a point on the parabola from the focus can be found by the distance formula and the distance of a point on the parabola from a horizontal or vertical line can be found by the absolute value of the difference between the abscissa or ordinate of the point on the parabola and the y- or x-value of the horizontal or vertical line. However, now that we have a formula for the distance between a point and any line with defined nonzero slope, we can create a parabola that is tilted at an angle. The way to do this would be to choose a directrix line $y=mx+b$ and a focus $(x_0, y_0)$, and the equation of the parabola would be

$$\sqrt{(x-x_0)^2+(y-y_0)^2}=\frac{\mid y-mx-b\mid}{\sqrt{m^{2}+1}}$$

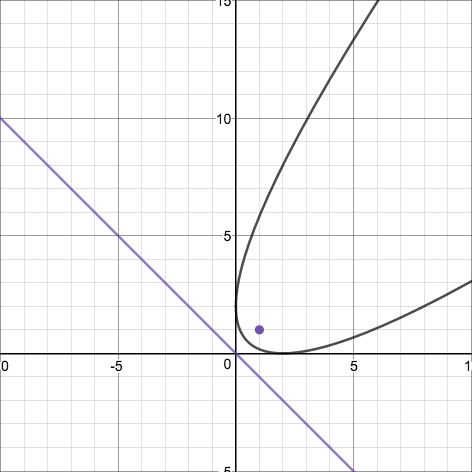
Let's try an example: the parabola with focus $(1,1)$ and directrix $y=-x$. First we must set up our equation:

$$\sqrt{(x-1)^2+(y-1)^2}=\frac{\mid y+x-0\mid}{\sqrt{(-1)^{2}+1}}$$ $$\sqrt{(x-1)^2+(y-1)^2}=\frac{\mid y+x\mid}{\sqrt{2}}$$

And now we must simplify. To begin, we square both sides.

$$(x-1)^2+(y-1)^2=\frac{(y+x)^2}{2}$$

Then we expand the binomials.

$$x^2-2x+1+y^2-2y+1=\frac{1}{2}y^2+\frac{1}{2}x^2+xy$$ $$\frac{1}{2}y^2-2y-xy+\frac{1}{2}x^2-2x+2=0$$ $$(\frac{1}{2})y^2+(-2-x)y+(\frac{1}{2}x^2-2x+2)=0$$

Now that we have this in $ax^2+bx+c$ form as a quadratic of y, we can solve it for y in terms of x using the quadratic formula.

$$y=2+x\pm \sqrt{(2+x)^2-2(\frac{1}{2}x^2-2x+2)}$$ $$y=2+x\pm \sqrt{x^2+4x+4-x^2+4x-4}$$ $$y=2+x\pm \sqrt{8x}$$ $$y=2+x\pm 2\sqrt{2x}$$

In this case, $y$ is not a function of $x$ because of the plus-or-minus, but the parabola can be represented as the two functions $2+x+2\sqrt{2x}$ and $2+x-2\sqrt{2x}$ together. Here is a graph of the parabola, along with its focus and directrix: