Skip to page content Home     Posts     CV     Contact     People

Distance from a Point to a Line

2016 Dec 1

Derive a formula for the distance from a point to a line in the cartesian coordinate plane.

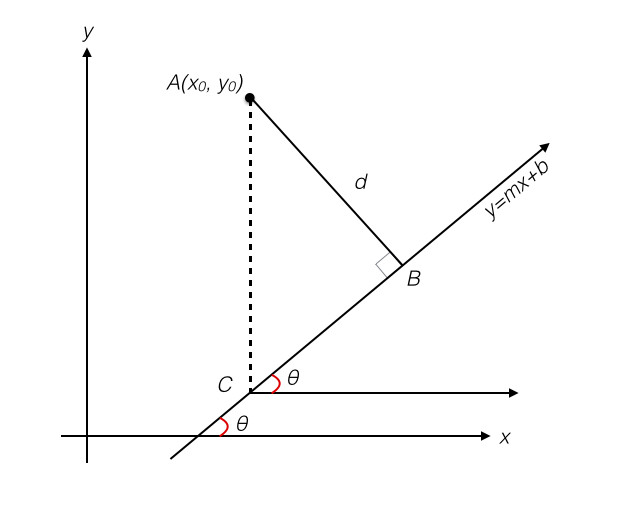
The distance from any point to a line is defined as the shortest distance between that point and any point on the line. The line segment connecting a point to its closest point on a line is always perpendicular to the line. Let the line be the line $y=mx+b$ with angle of elevation with the x-axis $\theta$ and the point be the point $A(x_0,y_0)$. Let $\overline{AB}$ be the perpendicular line segment from $A$ to $y=mx+b$, so that the distance $d$ is equal to the length of $\overline{AB}$. Let us also drop a vertical line segment $\overline{AC}$ from $A$ to $C$, the point on $y=mx+b$ directly above or below it. Finally, construct a line parallel to the x-axis through the point $C$. Now we have something that looks like this:

Now we can see that we have constructed a right triangle. Note that the angle that $y=mx+b$ makes with the horizontal line through $C$ is also $\theta$, since the horizontal line through $C$ is parallel to the x-axis and the line $y-mx+b$ acts as a transversal. Then, since $\overline{AC}$ is perpendicular to the horizontal line through $C$, $\angle{ACB}=90^{\circ}-\theta$. Since $\theta=tan^{-1}(m)$,

$$\angle{ACB}=90^{\circ}-tan^{-1}(m)=tan^{-1}(\frac{1}{m})$$

Also, since the ordinate of $A$ is $y_0$ and the ordinate of $C$ is $mx_0+b$,

$$\overline{AC}=\mid y_0-mx_0-b\mid$$

This is all we need to calculate $d$ using right triangle trigonometry:

$$sin(\angle{ACB})=\frac{d}{\mid y_0-mx_0-b\mid}$$ $$sin(tan^{-1}(\frac{1}{m}))=\frac{d}{\mid y_0-mx_0-b\mid}$$ $$\frac{1}{\sqrt{m^2+1}}=\frac{d}{\mid y_0-mx_0-b\mid}$$ $$d=\frac{\mid y_0-mx_0-b\mid}{\sqrt{m^{2}+1}}$$

Which gives us the distance between the point and the line.