Skip to page content Home     Posts     CV     Contact     People

Area of a Regular Polygon

2016 Nov 8

Derive a formula for the area of a regular polygon, given the side length and number of sides.

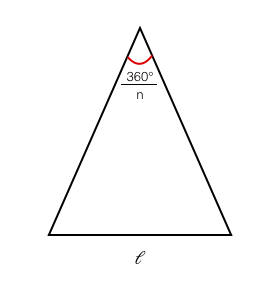
Let a regular polygon with n sides have side length l and apothem a. By a general formula, the area of this polygon is given by $$A=\frac{1}{2}lan$$ However, when finding the area of such a polygon, it can be tiresom to solve for the apothem given the side length and the number of sides, so we can make a general formula. If a cut is made from each vertex of the polygon to the center, it will be cut up into $n$ congruent isoscles triangles looking like this:

We can now cut each of these triangles in half with an altitute and end up with $2n$ right triangles that look like this:

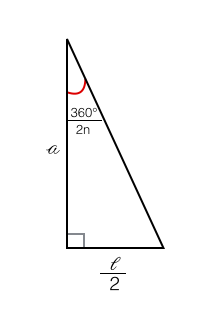
Now that we have a right triangle, we can use right triangle trigonometry to say that

$$tan(\frac{360}{2n})=\frac{l}{2a}$$ $$2a=\frac{l}{tan(\frac{180}{n})}$$ $$a=\frac{l}{2tan(\frac{180}{n})}$$

When we plug this into our original formula, we get

$$A=\frac{1}{2}lan$$ $$A=\frac{1}{2}l(\frac{l}{2tan(\frac{180}{n})})n$$ $$A=\frac{l^2n}{4tan(\frac{180}{n})}$$

Which gives us a formula for the area of a regular polygon given only the side length and the number of sides.