Schauergeschichten der Analyse
Fröhliches Halloween-Wochenende! Ich muss zugeben, daß alles Gruseliges und Gotisches mich immer interessiert hat und daß ich ziemlich viel krankhafte Neugier besitze. Diese Neigung beschränkt sich nicht nur auf die Horrorfilmen und die Gruselgeschichten sondern gilt sie auch für meine Interesse an der Mathematik. Während der frühesten höheren Mathematikkursen der Sekundarschule und der Universität lernt man viele schöne Theoreme und Methoden, die auf der Voraussetzung "hinreichend gut benommene" Funktionen beruhen. Aber jetzt, wo ich Lehrassistent für einen Rechenverfahrenskurs bin, und zwei Kursen über Real- und Fourieranalyse mache, habe ich verschiedene mathematischen Funktionen begegnet, die ausgesprochen schlecht benommen und sogar abscheulich sind. In diesem Blogeintrag werde ich einige "Ungeheuer" der mathematischen Analyse darstellen, die unseren üblichen numerische Methoden durcheinanderbringen und vor den alle angewandte Mathematiker sich fürchten... und in manchen Fällen, wie man sich vor ihr schützen kann.
Notiz: weil es so viele Beispiele gibt, die ich abbilden wollte, und weil ich so beschäftigt auch mit den Hausaufgaben bin, habe ich mir nicht die Mühe gegeben, Erklärungen für jeden aufzuschreiben. Die Meisten laße ich als Übungen oder Denkanregungen.
Das Newtonverfahren
Das Newtonverfahren ist ein Algorithmus zur Approximation der Lösung nicht linearen Gleichungen, im Besonderen im Form von
wo $f:\mathbb R \to\mathbb R$ "hinreichend gut benommen" ist. Zum Beispiel, wenn $f(x)=x^2-2$, bietet das Newtonverfahren eine Approximation von $\sqrt{2}$. Der Algorithmus läuft folgenderweise: wir definieren eine Folge von Approximationen $x_0,x_1,x_2...$ vermittels der Rekursionsgleichung
wo $x_0$ eine Schätzung ist, die "hinreichend nah" zur wirklichen Wurzel steht. Graphisch interpretiert ist $x_{n+1}$ die Wurzel der Gerade, die $f(x)$ am besten in der Nähe von $x_n$ approximiert, also der Berührungslinie.
Für die meisten "angenehme" Funktionen hat das Newtonverfahren quadratischer Konvergenzordnung, wie zum Beispiel $f(x) = x^2-2$. In diesem Fall ist die Rekursionsgleichung
Mit der Schätzung $x_0 = 1$ läuft die Folge so:
Ausgezeichnet! Der Stellenzahl von Genauigkeit ist mit jeder Wiederholung verdoppelt. Betracht mal jetzt die Funktion $f(x) = (x^2-2)^2$, die die gleiche Wurzel $x=\sqrt{2}$ besitzt. Von dieser haben wir die Rekursionsgleichung
die die folgende Folge hervorbringt:
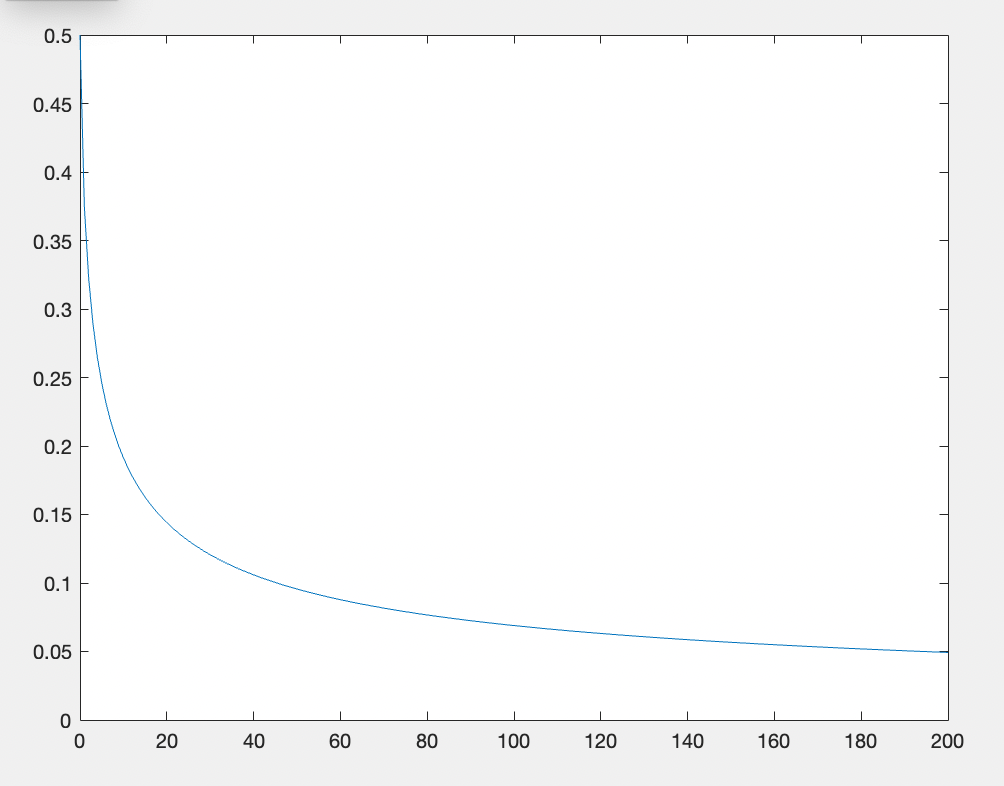
In diesem Fall die Genauigkeit steigt nur linear. Auch für die Funktionen $f(x) = (x^2-2)^m$ wo $m\in \mathbb N\backslash {1}$. Im Allgemeinen funktioniert das Newtonverfahren nicht richtig wann $f$ eine mehrfache Nullstelle hat. Die Genauigkeit kann auch sehr langsamer als linear steigen - z.B. für die Funktion $f(x)=e^{-1/x^2}$, die die Wurzel $x=0$ hat, nimmt der Schätzfehler sehr langsam ab:
Es gibt auch Funktionen, für die die Nähe von $x_0$ zur wahrhaften Nullstelle gar keine Konvergenz garantiert. Schau mal dieses Monster an:
Die hat unendlich viel Extrema in der Nähe von der Nullstelle $x=0$, in der Nähe von denen die Berührungslinie von $f$ fast flach ist. Solange $x_0$ ausreichend nah zu einem Extremwert steht, kann der Schätzfehler von $x_1$ größer als die von $x_0$ sein. Zu allem Übel gibt es auch $x_0$ in jeder Umgebung der Wurzel, für den das Newtonverfahren eine periodische Folge $x_0, x_1, x_0, x_1, ...$ hervorbringt! (Kannst du diese Tatsache analytisch beweisen?)
Tatsächlich ist jeder der obenen Gegenbeispiele ziemlich "gut benommen" - jedes ist sogar $C^\infty$! Also, was genau erfordert das Newtonverfahren von einer Funktion? Der wirkliche Theorem lautet folgendermaßen:
Wenn $f:\mathbb R \to \mathbb R$ stetig differenzierbar in einer Umgebung von der Nullstelle $x=\alpha$, $f'(\alpha)\ne 0$ und $f''(\alpha)$ existiert, dann konvergiert das Newtonverfahren quadratisch.
Die Polynominterpolation
Zu jeder Menge von $n$ Punkte ${(x_j,y_j)}$ entspricht ein einziges Polynom $P$ $n-1$ -ten Grades, das sie interpoliert, damit $P(x_j) = y_j$ für alle $j=1,2,...,n$, solange alle $x_j$ verschieden sind. Deshalb wenn $f:\mathbb [a,b]\to\mathbb R$ irgendeine Funktion ist, können wir immer ein Polynom $P:[a,b]\to\mathbb R$ $n-1$ -ten Grades auch finden, das an $n$ vorgeschriebenen Punkte $x_1,...,x_n$ gleichwertig wie $f$ sind, sodaß $P(x_j) = f(x_j)$. Unter bestimmten Bedingungen wird $P$ auch nah (doch nicht gleich) zu $f$ sonst überall in $[a,b]$ kommen... aber nicht immer.
Zum Beispiel, im Interval $[-1,1]$, die Funktion $f(x)=e^x$ läßt sich sehr gut von Polynomen interpolieren: mit nur $n=6$ Punkten sinkt der Maximalfehler der Interpolante niedriger als $10^{-5}$ und mit $n=9$ Punkten niedriger als $10^{-8}$. Unten siehst du den Graph des Fehlerwerts $|e^x - P_n(x)|$ im Interval $[-1,1]$ für $n=3,6,9,12$:
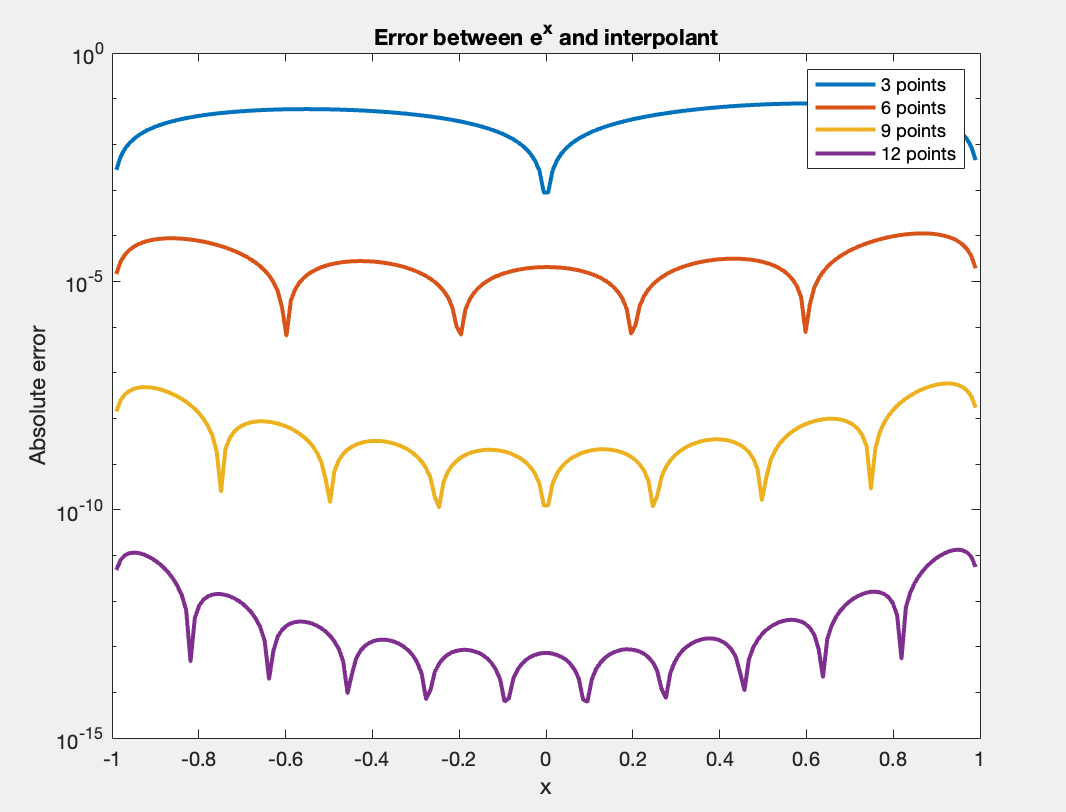
und hier findest du einen Graph des Maximalfehlers für jeder $n$:
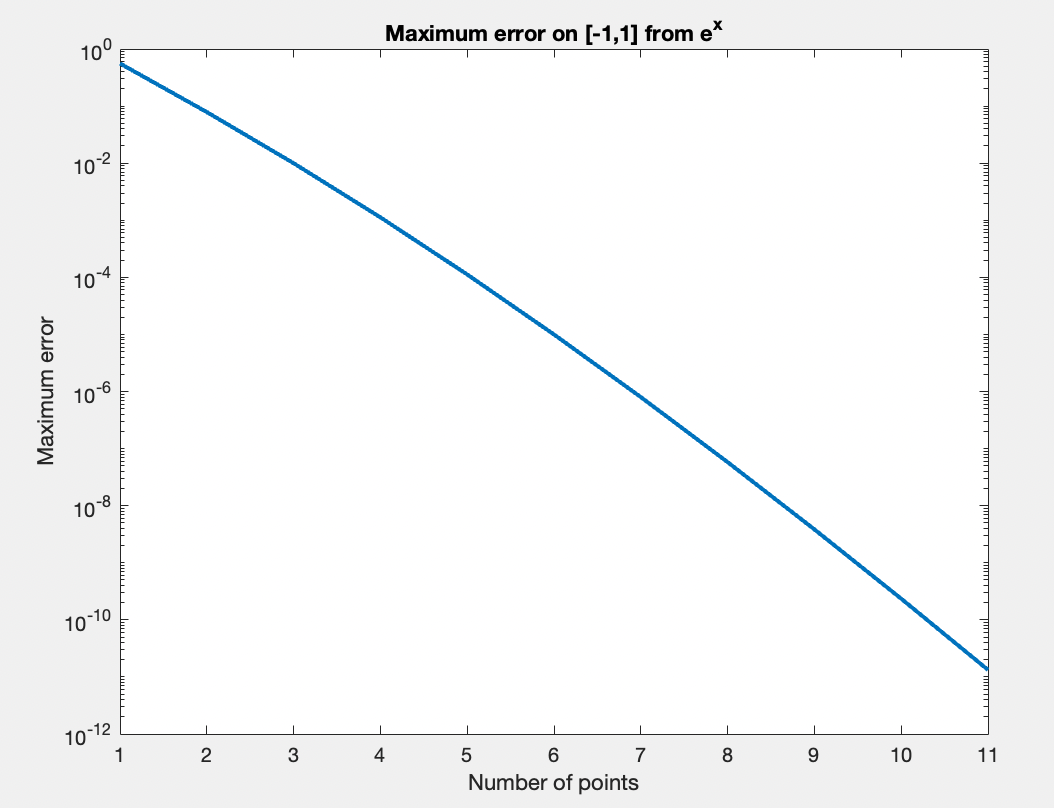
Schön! Aber für andere Funktionen funktioniert diese Methode der Polynominterpolation nicht so gut. Zum Beispiel die Funktion
laßt den folgenden Maximalfehlergraph entstehen:
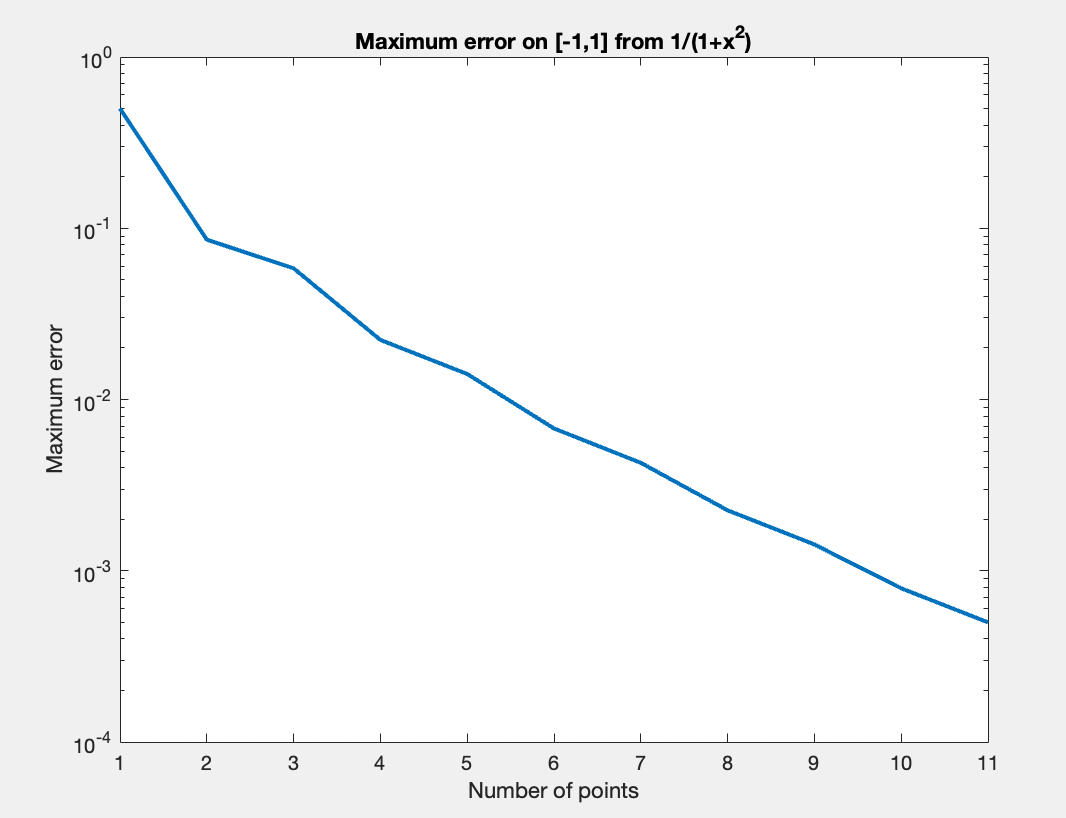
Es sieht so aus, als ob diese Polynomen auch konvergieren, nur aber ein bisschen langsamer. Betracht mal jetzt die Funktion
die dem folgenden Fehlergraph entspricht:
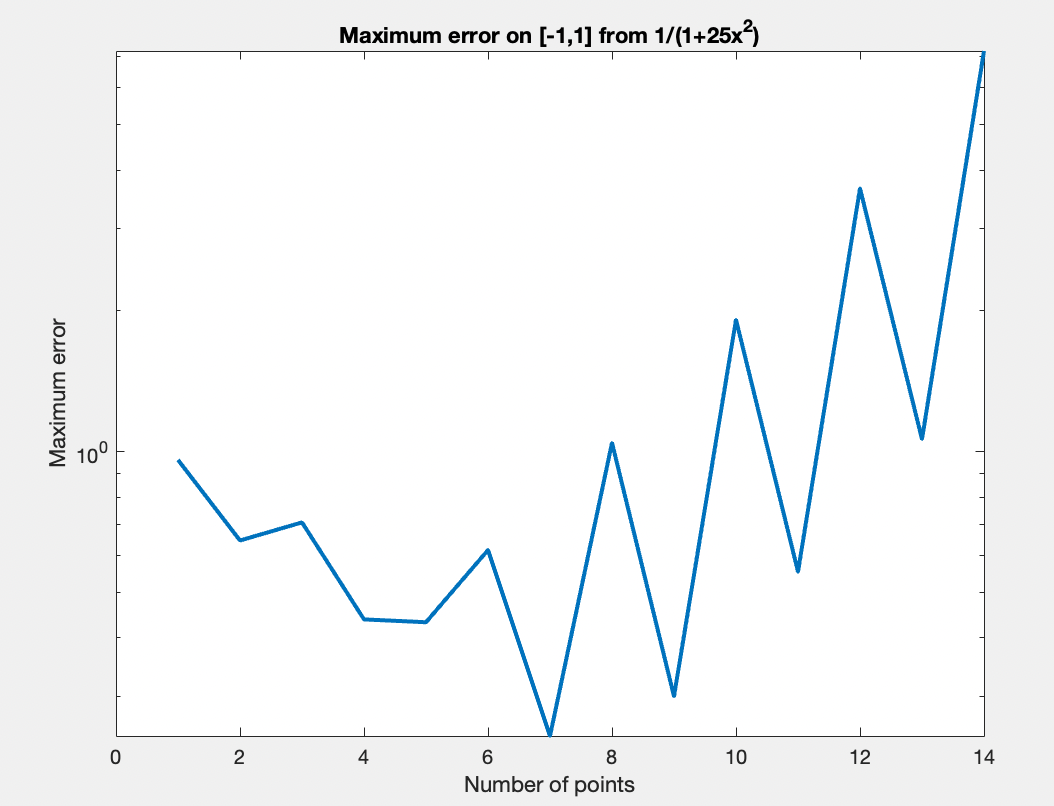
Was ist hier passiert? Obwohl diese Funktion ziemlich "gut benommen" ist - also, kontinuierlich und stetig unendlich oft differenzierbar - konvergieren seine Interpolante gar nicht und sowohl schlechter werden als $n$ steigt. Hier findest du ein Graph mit der Funktion $f$ und ihrer Interpolante mit $n=12$:
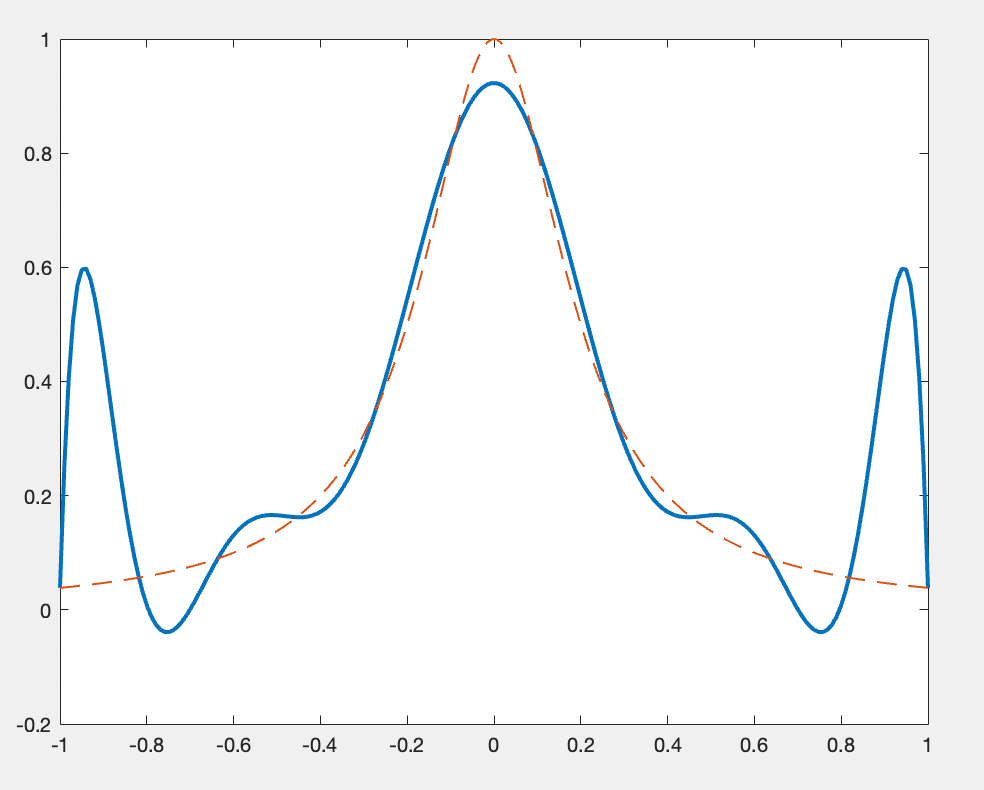
Aus irgendeinem Grund schwankelt die Interpolante unbeherrschbar in der Nähe von den Intervallgrenzen. Diese Besonderheit heißt Runges Phänomen. Was ist hier los? Warum überhaupt gibt diese bestimmte Funktion sich nicht zum Polynominterpolation her?
Vermittels des Satzes von Rolle kann man beweisen, daß wenn $f$ glatt ist, ist der Fehler der Polynominterpolante mit $n+1$ Punkten $x_0<...<x_n$ gleich
wo $\xi$ ein bestimmten Zahl im Intervall $[x_0,x_n]$ ist, solange $x\in [x_0,x_n]$ auch. Wenn $x_0=-1$ und $x_n=1$ und die gleichmäßig verteilt in $[x_0,x_n]$ sind, daraus folgt, daß
und damit kann man auch beweisen, daß
und deshalb
Infolgedessen konvergieren die Interpolanten $P_n$ solange $|f(x)-P_{n}(x)|\to 0$ als $n\to\infty$ für jeder $x\in [x_0,x_n]$, derentwegen würde die Bedingung ausreichen, daß
also, daß $|f^{(n+1)}(\xi)|$ nicht "superschnell" steigt als $n\to\infty$. Mit der Funktion $f(x)=e^x$ ist diese Bedingung ideal, weil in diesem Fall $f^{(n+1)}(x)=e^x$ auch und deshalb
für alle $\xi\in [-1,1]$. Für $f(x) = \frac{1}{1+25x^2}$ steigen $f^{(n+1)}(\xi)$ viel schneller: im Besonderen
und derentwegen
...also, unsere Bedingung wird gar nicht erfüllt. Wir beschließen, daß die Glätte der Funktion $f$ keine Konvergenz der Polynominterpolanten garantiert, weil auch wenn die Ableitungen $f^{(n+1)}$ existieren überall, können die Interpolanten "unkontrollierbar schwankeln" wenn $f^{(n+1)}$ "zu groß" sind.
Die Fourierreihe
Die Fourierreihe einer periodischen Funktion $f:\mathbb R\to\mathbb R$ ist die reihe
wo die Fourier-Koeffizienten $\hat{f}(n)$ sind
Der grundlegenden Theorem der Fourieranalyse behauptet daß solange $f$ eine "angemessene" periodische Funktion ist, konvergiert seine Fourierreihe gegen sich selbst:
Laut der Professorin meines Fourieranalysenkurses war die Hauptfrage der Fourieranalyze lange Zeit "was genau heißt angemessen?" Also, welche Beschränkungen wirklich garantieren, daß die Fourierreihe einer Funktion konvergiert? Eine glaubhafte Vermutung: vielleicht kann es sein, daß die Kontinuität punktweise Konvergenz der Fourierreihe garantiert. Erstaunlicherweise aber gar nicht. Tatsächlich habe ich eine solche Grässlichkeit als Abschlussproject für den Kurs erdacht - wenn dieses Thema dich interessiert, hier findest du einen Entwurf meines Projects.
Trotz der Tragik dieser kontraintuitiven Ergebnis gelang es mir zu beweisen, daß alle kontinuierliche Funktionen außer die "schlechteste" konvergente Fourierreihen haben. Nämlich klappt es für all Lipschitz-Funktionen und Hölder-kontinuierliche Funktionen, also, alle Funktionen die nicht "steiler" als eine Potenzfunktion sind. Außerdem klappt es für alle lokalmonoton Funktionen. Deshalb muß jeder Gegenbeispiel "sehr steil" und "grenzenlos wackelnd" in der Nähe von einem Punkt sein.
Wir haben auch das folgende Resultat in meinem Fourieranalysenkurs bewiesen:
Solange $f:\mathbb R\to\mathbb R$ $2\pi$ -periodisch und stetig differenzierbar ist, konvergiert seine Fourierreihe überall.
Dieses ist aber ein schwächeres Resultat, als das was ich in meinem Projekt demostriere, weil alle differenzierbare Funktionen local Hölder-kontinuierlich sind, aber das Gegenteil ist nicht wahr. Man kann auch beweisen, daß obwohl die Kontinuität kein Konvergenz der Fouriersummen $S_n f$ garantiert, zieht sie etwas schwächer aber trotzdem interessant nach sich:
Solange $f:\mathbb R\to\mathbb R$ $2\pi$ -periodisch und kontinuierlich ist, konvergieren die Durchschnitte ihrer Fouriersummen:
Ausgang
Wir haben hier demonstriert, daß obwohl eine Funktion anscheinend "gut benommen" auf den ersten Blich aussieht, sei es kontinuierlich, differenzierbar, oder glatt, kann es andere Eigenschaften besessen, die die übliche numerische Methoden versauen, z.B.:
- mehrfache Nullstellen
- unendliche Schwankungen in der Nähe eines Punktes
- schnell steigende Ableitungen
- extrem Steilheit
Lass dir das eine Lehre sein... wenn du eine numerische Technik auf einer Funktion das nächste Mal anzuwenden versuchst, Vorsicht! Es kann sein, daß deine Funktion eine von diesen verkleideten Ungeheueren ist... (zwar ist es aber ziemlich unwahrscheinlich.)
