Franklin Pezzuti Dyer

Three semesters of projects

My second year of college at UNM is over, and I've been extremely busy! Sadly, this means I haven't had time to write as many blog posts as I've wanted about the interesting topics I've been exploring in school and during my free time. I'm hoping to write a post or two this summer, but for now I'm just putting out a short post to show off some of the (non-blog) projects I've been working on, roughly in chronological order. Even if I won't have time to write in-depth blog posts about these topics, I've spent a lot of time on them over the past couple semesters, so it feels like they should appear on my blog somewhere.

Turtle geometry and 3D printing

During Fall 2020 and Spring 2021, I worked with Professor Leah Buechley at the Hand and Machine lab. At first, I spent a lot of time learning how to use a 3D printer and manipulate STL and GCODE files. An STL file is used to store the coordinates of points in 3D space, usually representing the vertices of some polyhedron or points distributed across a curved surface. These files are digital representations of 3D solids, and the can be passed as input to slicer software, which generates a sequence of instructions (in the form of a GCODE file) telling the 3D printer how to manufacture the represented solid by depositing plastic layer-by-layer. I wrote about STL files and their format in this blog post, and this presentation shows some of my experiments with directly writing GCODE files without the aid of a slicer.

After getting more familiar with 3D printing, I worked with Dr. Buechley to design a Python library called ExtruderTurtle. Traditional design techniques for 3D-printed objects focus on their high-level global geometry, which is necessary to some extent for 3D printing in order to avoid mishaps such as the 3D printer nozzle colliding with the plastic sculpture. However, in the spirit of the Turtle Geometry paradigm, this library encourages users to focus on the local geometry of their 3D prints, such as texture and flexibility, by describing all 3D printer nozzle movements relative to the previous position rather than in a global coordinate system. You can read more about the library and see some demonstrations at this page. We also wrote a paper about our library which was published in the proceedings of TEI 2022 - you can read our paper here.

As a teaser, here's a picture of some cool prints created using the ExtruderTurtle library:

Fluid dynamics

In Spring 2021, I took MATH 375, a numerical computing class at UNM that covered topics such as floating point arithmetic, numerical differentiation and integration, and algorithms for linear algebra. This class was taught by Professor Monika Nitsche, and thanks to her recommendation, I've been able to TA/grade for this class for the past two semesters! (But that's another story.) I also got involved in Professor Nitsche's research involving computational fluid dynamics and applied for the ASSURE research fellowship at UNM. For a while, I learned about her research involving the behavior of multiple nested droplets of varying viscosities/surface tensions in Stokes flow. Eventually, however, I started working on an individual project modeling potential flow past an elliptical cylinder and how it can be used to approximate potential flow past a plate. This project culminated in a research report and a poster presentation last April.

Check out this potential flow past a cylinder:

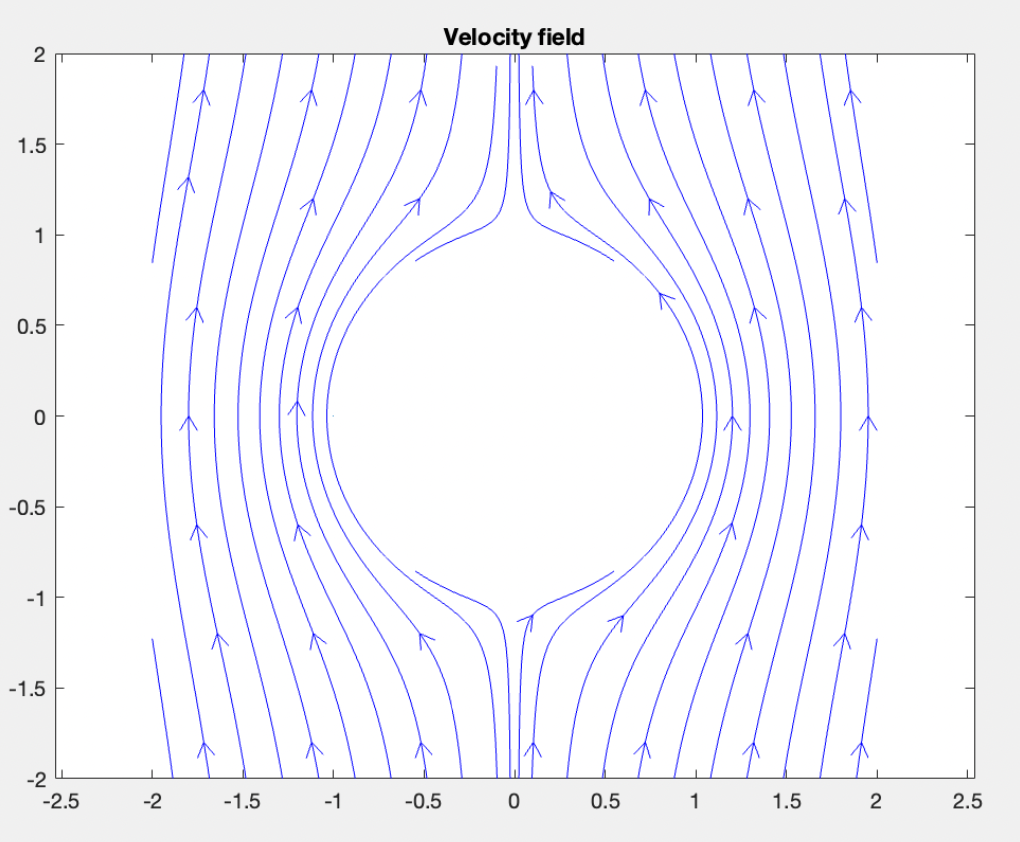
and here's another potential flow past a cylinder, this time with nonzero circulation so that it "wraps around" the cylinder:

Fourier analysis project

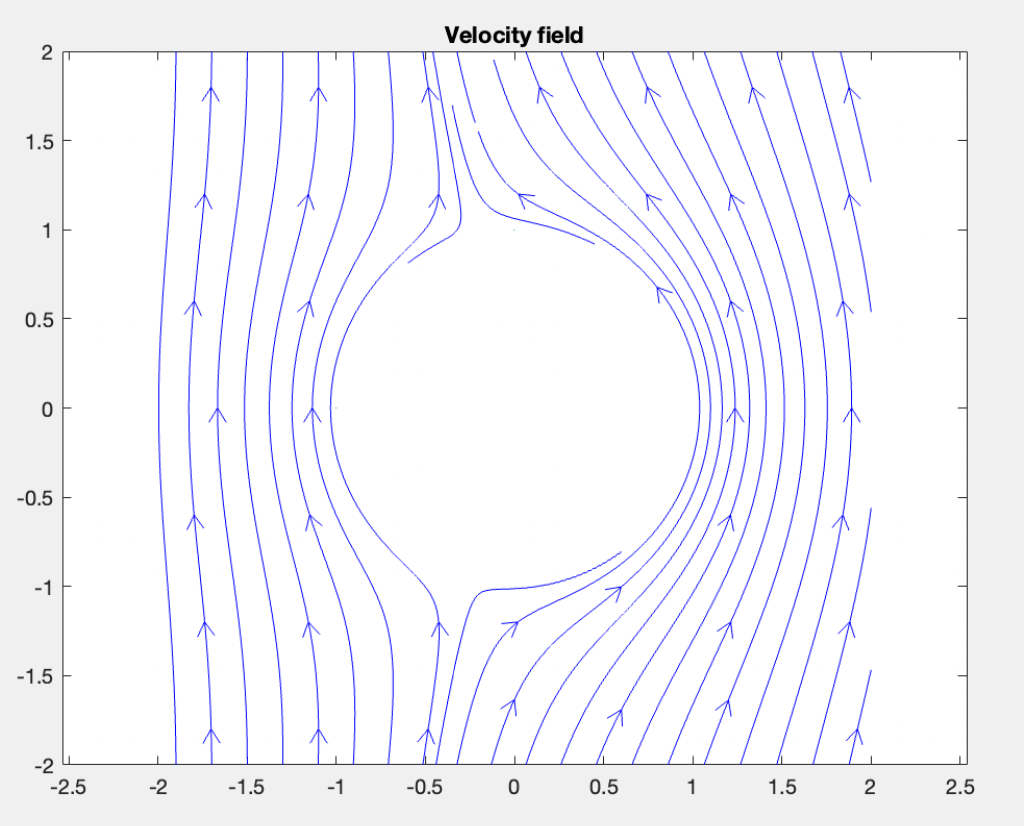
Last semester I took a class on Fourier analysis - another topic I've been yearning to learn about since high school. One of the first things we discussed in the class was the question of exactly which periodic functions have a Fourier series. We proved easily that all functions in $C^2(\mathbb T)$, that is, all twice continuously differentiable functions, have an everywhere convergent Fourier series. With a bit more difficulty, we showed that the weaker condition of continuous differentiability is also sufficient. Amazingly, however, continuity is not sufficient for a function to have a pointwise convergent Fourier series. The professor (Dr. Pereyra, who I'm currently doing my honors thesis with) mentioned this bizarre fact offhand but we didn't prove it in class, so I started trying to construct pathological functions on my own, with the goal of finding a continuous function whose Fourier series diverges at a point.

In the end, I managed to find one, and as my final project for the class, I wrote a detailed description of its construction. The professor encouraged me to do a "literature search" to see if anyone else had come up with the same construction in the past, or if my construction was a new one. The first proof of this result (that I know of) was by DuBois-Raymond in 1873, so I looked up his paper in the archives (in German!) to compare notes. And, lo and behold, DuBois-Raymond had come up with almost exactly the same construction as I did. It was amazing to think that, almost $150$ years later, I stumbled upon the same construction as this German mathematician from the 1800s!

Category theory DRP

During my freshman year at UNM, my friend Austin Bell, a pure math graduate student at UNM, came up with the idea of starting a Directed Reading Program at UNM. The program is meant to seek out undergraduate students who would like to learn about a certain math-related topic outside of class, either because UNM doesn't offer a class on that topic or because of the greater flexibility/gentler pace of self-study, and pair these students with graduate student mentors to help them work their way through an advanced book on that topic. After Austin and I worked together to set up this program last year, I participated in a DRP on complex analysis, where I worked through Ahlfors' Complex Analysis with my mentor Owen Davis. My previous blog post on elliptic functions, which I'd been itching to learn more about since high school, was a product of what I learned in this DRP.

One of the reasons I haven't had time to write many blog posts this semester is because I've been occupied with a DRP on a different topic this semester, namely category theory. Category theory is sometimes described as an alternative foundation for mathematics that takes a "top-down" perspective, as opposed to set-theory's way of constructing mathematical structures from the "bottom up". We started by reading Emily Riehl's Category Theory in Context, but at this point I've moved on to Saunders MacLane's Categories for the Working Mathematician, which I find to be written more clearly and better-organized. I've also started learning about type theory, using Homotopy Type Theory from the Univalent Foundations Program as my textbook. This has given me the chance to apply what I know about category theory to computer science and programming, in particular using Haskell, which I started learning in class this semester, and Coq, which I've been toying with for the past couple weeks. You can read my solutions to some category theory and type theory exercises in this PDF.

Actually, because of a funny turn of events, I ended up being a DRP mentor this semester as well. I spent most of last winter break self-studying set theory and model theory (you can read my notes here), because my real analysis class in Fall 2021 piqued my interest in math foundations. Then, during DRP signup at the start of the Spring semester, one undergraduate chose set theory and foundations as their preferred topic. I don't know of any graduate students at UNM who study set theory or math foundations, so I offered to be his mentor despite only being an undergrad myself. He decided to take me up on the offer, so we've been working through Sierpinski's Cardinal and Ordinal Numbers and Chang and Kiesler's Model Theory all semester. My mentee caught up to me extremely quickly, and I really enjoyed having someone to explore the mind-bending intricacies of set and model theory with. Set theory and model theory have also had some interesting interplay with my studies in category theory.

Honors thesis on growth orders

For the past few months, aside from the time I've been putting into category theory, I've been hung up on a couple tricky problems of personal interest from real analysis, specifically involving asymptotics and growth orders. I wrote two blog posts (first, and second) about my attempts two formalize my questions and tentative solutions, but shortly after finishing the second post I decided to start writing up my definitions and proofs more formally. I'd gotten to the point where I couldn't keep it all in my head, and if I tried to rely on the chicken-scratch ramblings from my notebook, I'd inevitably make a mistake at some point and lead myself up the garden path. So I started compiling definitions and propositions in a LaTeX document.

Before I knew it, I'd accumulated about 50 pages of notes. Needing a sanity check, I spoke with Professor Cristina Pereyra about the problems I was working on, and she said that my project would make a good undergraduate honors thesis! Now I've turned my personal interest project into a work-in-progress honors thesis, and I'm doing an independent study course with Dr. Pereyra to get her advice and feedback on my work. I'm really enjoying it, and I'm grateful that she has time to help me improve my proofs/exposition and flesh out my weird ideas!

As a teaser, here's a pleasing diagram that I created for my thesis:

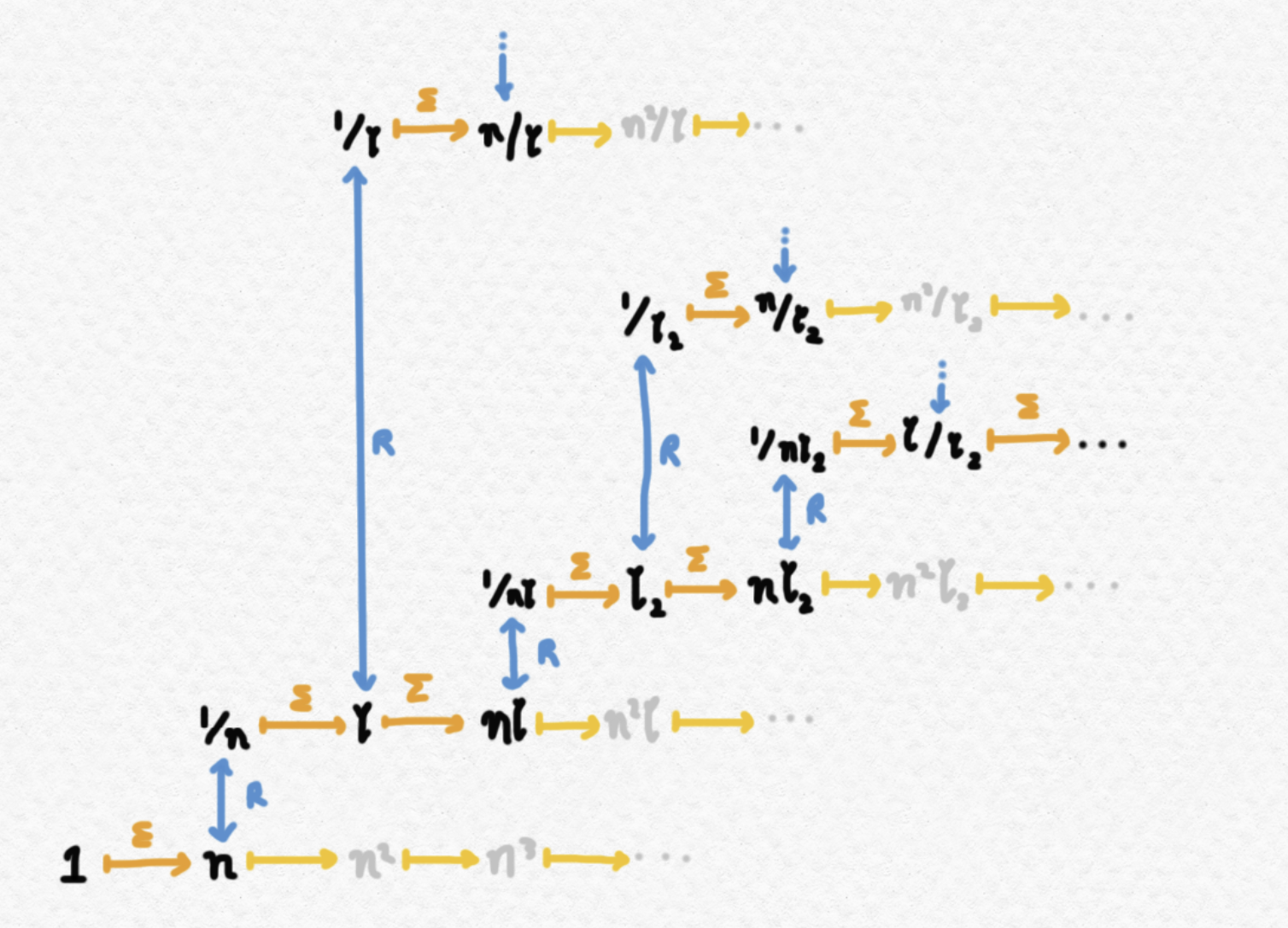
What on earth does this diagram mean, and what does it have to do with growth orders, you might ask? Each of the symbols in black/gray with arrow to/from it represents a growth order, such as $\Theta(n)$, $\Theta(n\log n)$, or $\Theta(\log\log n)$. (These are denoted by $\mathfrak n$, $\mathfrak{nl}$, and $\mathfrak{l}_2$ respectively.) The arrows between growth orders indicate that one growth order is the reciprocal of another, or the growth order of the sequence of partial sums of another. For instance, the orange arrow from $1/\mathfrak{nl}$ to $\mathfrak{l}_2$ represents the asymptotic identity $\sum_{k=2}^n \frac{1}{k\log k}=\Theta(\log\log n)$ This diagram is my way of visualizing the treelike structure that results from repeatedly taking reciprocals and partial sums of growth orders, which I'm studying in-depth in my thesis. You can read my current draft at this link.

Summary

It's been a fun couple of semesters! Here's a list of links to the projects I've been working on that you can access on my blog:

For the next two semesters, I'll be studying abroad at the Universidad de Granada in Spain. That will be a whole new adventure to write about!