(Psst! Don't want to read this in Spanish? Here's a translation.)
Hay una idea que se remonta a la filosofía griega que el índole esencial de la verdad es que es lo que perdura a lo largo del tiempo mientras que todo lo demás se va cambiando. Como matemático tanto como informático me parece muy apto esa idea. A mi parecer la motivación principal de hacer una demostración formal de algún hecho lógico o matemático es la seguridad de poder contar con ese hecho para siempre. Hay esa filosofía platónica de que existe una verdad matemática que ha existido siempre y cuya veracidad no depende de quien lo sepa pero ¿qué nos vale una hecho que no tenemos entre las manos? ¿Por qué asumir que una aserción o es cierto o es falso hasta antes de saber cuál es?
Bueno, nunca he sido muy platónicamente inclinado pero no me pongo a discutir las ventajas de la metafísica constructiva versus la platónica. Lo que sí quiero tratar es un intento de renovar la lógica proposicional (y la teoría de conjuntos) clásica para hacerla más compatible con el punto de vista constructivo, que tal vez aún al platonista le interesaría si sólo por el montón de nuevos problemas interesantes que produce. Si te interesa la entrada y quieres leer más, te sugiero el libro Topos theory por Robert Goldblatt que es un libro muy accesible y bien escrito (del cual aprendí de estas cosas por primera vez) que aborda tanto la lógica como los fundamentos de la teoría de categorías.
Para representar el tiempo usaremos un conjunto de "instantes" $\mathbb P$ con un orden parcial $\le$ para que $x < y$ indica que el momento $x$ ocurre (estrictamente) antes del momento $y$. A $\mathbb P$ nos referimos como el marco de la lógica. Si $\Sigma$ es un conjunto se sentencias que o pueden ser ciertos o no en cada instante, tendremos una función $f:\mathbb P\to 2^\Sigma$ que devuelve el conjunto de sentencias que son ciertos en cualquier momento. Nuestro postulado que la verdad perdura por el tiempo se puede formalizar con una condición sencilla en la función $f$: si $x \leq y$ entonces $f(x)\subseteq f(y)$.
Tal vez te preguntas por qué permitimos que $\mathbb P$ sea un orden parcial en vez de un orden total. ¿Qué sentido tiene un marco con dos "momentos" de tiempo que no son equiparables, o sea, tal que ni el uno ni el otro ocurre antes o después? Pues imagínate que un equipo de matemáticos constructivos anda demostrando cosas de un momento al otro y así se va creciendo su cuerpo de conocimiento, o sea el conjunto $f(t)$. Pero algún día se dan cuenta de que su teoría no es bastante fuerte para abordar todos los problemas que les interesan así que tendrán que añadir otro axioma a su teoría. Pero si no están todos de acuerdo respeto a cuál axioma deben elegir, los matemáticos se repartirán en varios grupos cada uno de los cuales alimenta sus exploraciones matemáticas con un nuevo axioma distinto. Esa fractura se puede representar a través de una bifurcación en el marco $\mathbb P$: dependiendo de qué axiomas eligen los grupos distintos es posible que sus teorías ya no serán consistentes entre si. Así que, un marco no sólo vale para modelar el desarrollo de una teoría en el tiempo sino también varias teorías alternativas (o "realidades posibles" si quieres). Como informático esta construcción me recuerda de los diagramas que se puede dibujar de un repositorio de GitHub para mostrar las ramas distintas de un proyecto - tal vez sería útil este tipo de lógica para rastrear cómo se desarrollan las funcionalidades de ramas distintas de un proyecto de programación.
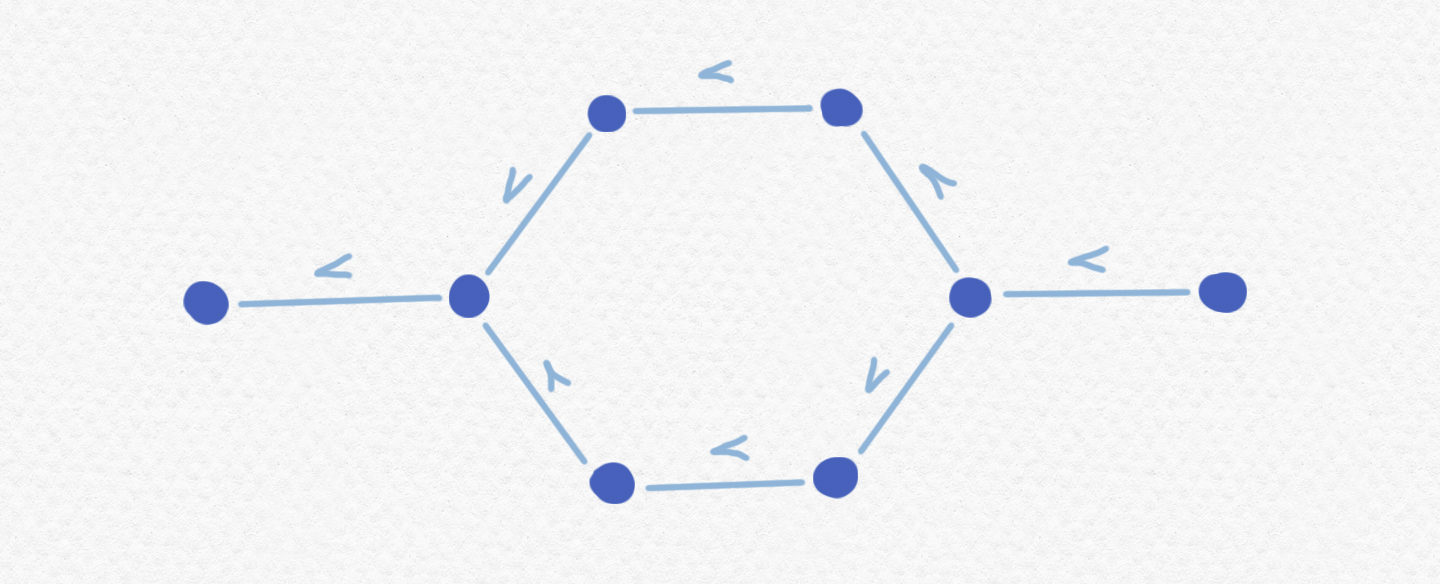
En la lógica clásica existen sólo dos valores de verdad: una sentencia o es cierto o es falso y si somos simpatizantes a los constructivas tal vez diríamos "no cierto" en vez de "falso". Pero ¿qué tal en un marco? ¿Cuántos "comportamientos distintos" puede tener una sentencia $\sigma$ en un marco $\mathbb P$? En esta formalización más complicada hay que tener en cuenta no sólo si una sentencia es cierto o no sino si es cierto o falso en cada instante, es decir que el valor de verdad de una sentencia $\sigma$ se define como el subconjunto de momentos de $\mathbb P$ en los cuales sí es cierto $\sigma$. Consideramos el marco $\mathbb P$ como un ejemplo sencillo:

Como dije, hay que considerar todas las combinaciones posibles de estar cierto y no estar cierto en cada momento de $\mathbb P$. Eso indica que hay a lo máximo $2^{|\mathbb P|}$ valores de verdad pero no podemos deducir que eso es el número exacto puesto que algunas combinaciones no serán posibles debido al requisito que lo cierto perdura en el tiempo. Por ejemplo, no es posible que una sentencia $\alpha$ sea cierto en el primer momento y no en el último. Aquí está una lista de todos los subconjuntos de $\mathbb P$ que pueden ser valores de verdad para alguna sentencia $\alpha$:
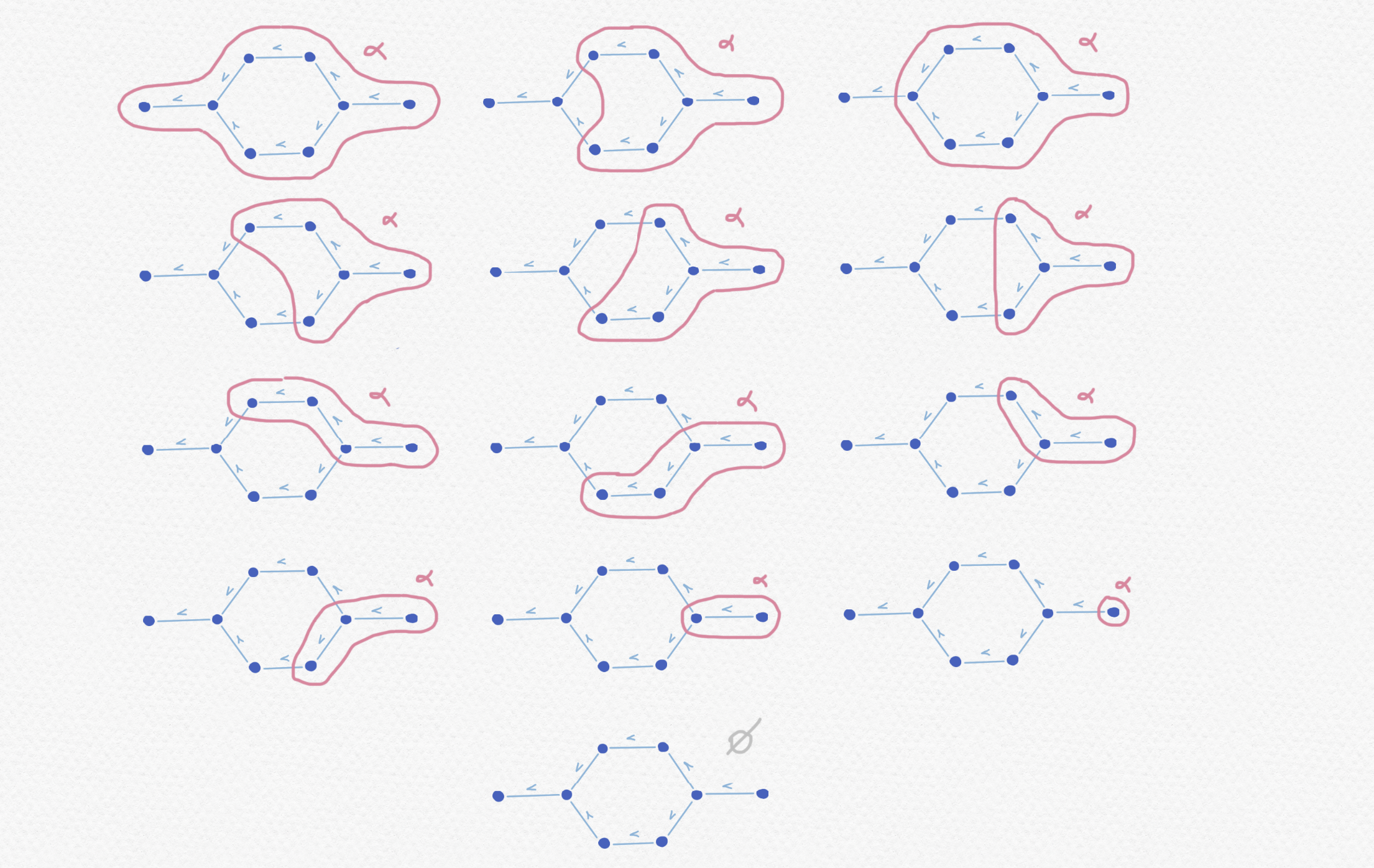
Así se puede describir los valores de verdad de un marco $\mathbb P$ como subconjuntos $V\subset \mathbb P$ con la propiedad de que "sus elementos perduran", o sea, $x\in V$ implica que $y\in V$ para cada $y\ge x$. Ese tipo de subconjunto de un conjunto parcialmente ordenado se llama una sección final.
Fíjate que aún desde ese marco $\mathbb P$ bastante sencillo surgieron hasta $13$ valores de verdad. Como ya hemos notado no es posible tener más que $2^{|\mathbb P|}$ valores pero por otro lado para cada $n$ existe un marco $\mathbb P$ que produce $2^n$ valores de verdad (en particular el orden parcial trivial en el que ningún par de elementos es comparable). Así que la complejidad de calcular los valores de verdad de un marco (finito) podría ir creciendo de manera exponencial. De todos modos existen técnicas más eficiente que fuerza bruta de calcular el número de valores de verdad de un orden parcial finito. Por ejemplo, si no me equivoco el número de secciones finales distintas del marco
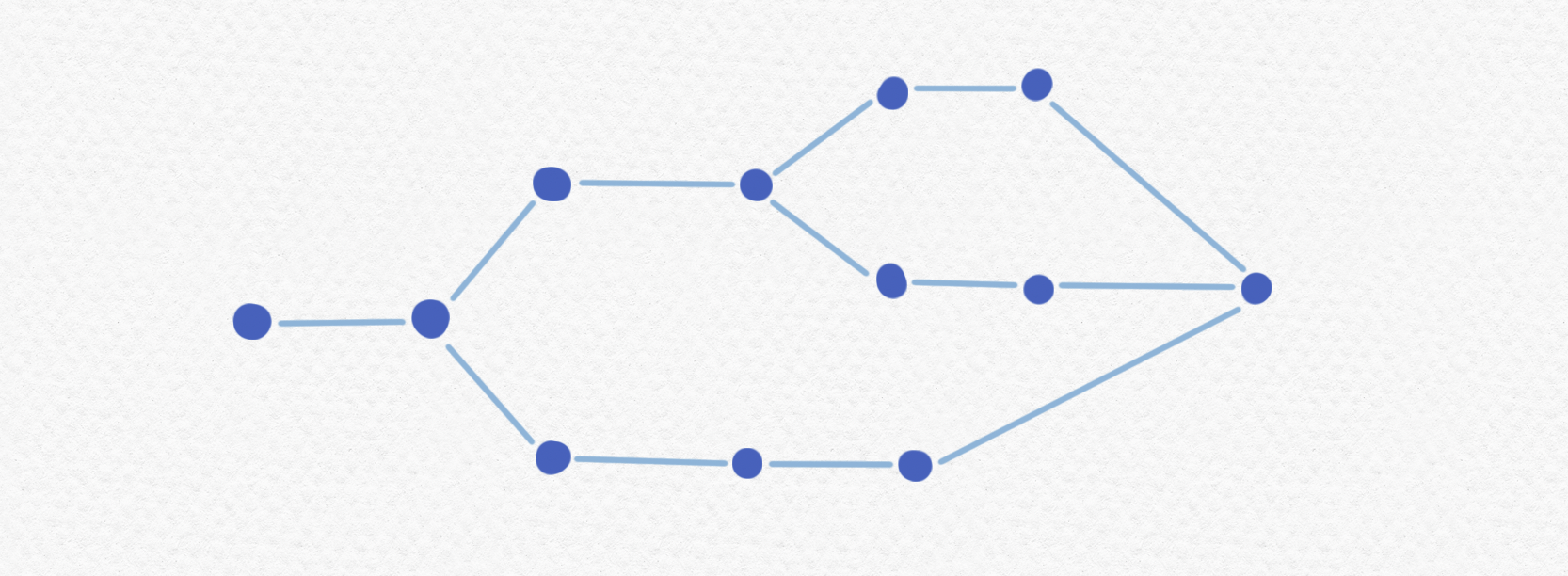
será $47$. ¿Puedes verificar tú esa cifra?
Pues si queremos que este sistema sea una alternativa a la lógica clásica necesitaremos definir operaciones correspondientes a las operaciones lógicas clásicas de "y", "o", "no" y "entonces" para poder hacer cálculo con las valores de verdad. Como ellos se identifican con secciones finales del marco $\mathbb P$ podemos definir esas en términos de operaciones con conjuntos asegurándonos de que el resultado de aplicar cada operación a una sección final o dos secciones finales produce otra sección final (en vez de otro subconjunto del marco que no sea sección final).
Si $\alpha$ y $\beta$ son sentencias con valores de verdad $U,V\subset\mathbb P$ podemos definir los valores de $\alpha\land\beta$ y $\alpha\lor\beta$ fácilmente usando las operaciones de intersección y unión de conjuntos. Definimos el valor de verdad de $\alpha\land\beta$ como $U\cap V$ o sea el subconjunto de $\mathbb P$ que consta de los momentos en los cuales $\alpha$ y $\beta$ ambos están ciertas. Si $\alpha$ y $\beta$ ambos están ciertas en algún instante claro que ambos también estarán ciertas en todos los instantes que siguen puesto que cada una perdura en el tiempo, así que $U\cap V$ es una sección final como deseamos. Semejantemente si $\alpha$ está cierta o $\beta$ está cierta en algún momento entonces una de las dos lo estará en cada momento del futuro, particularmente lo mismo que está cierto en el momento actual. Así que definimos el valor de verdad de $\alpha\lor\beta$ como $U\cup V$ que es otra sección final. Fíjate que forman las secciones finales un retículo puesto que podemos tomar uniones e intersecciones de ellas.
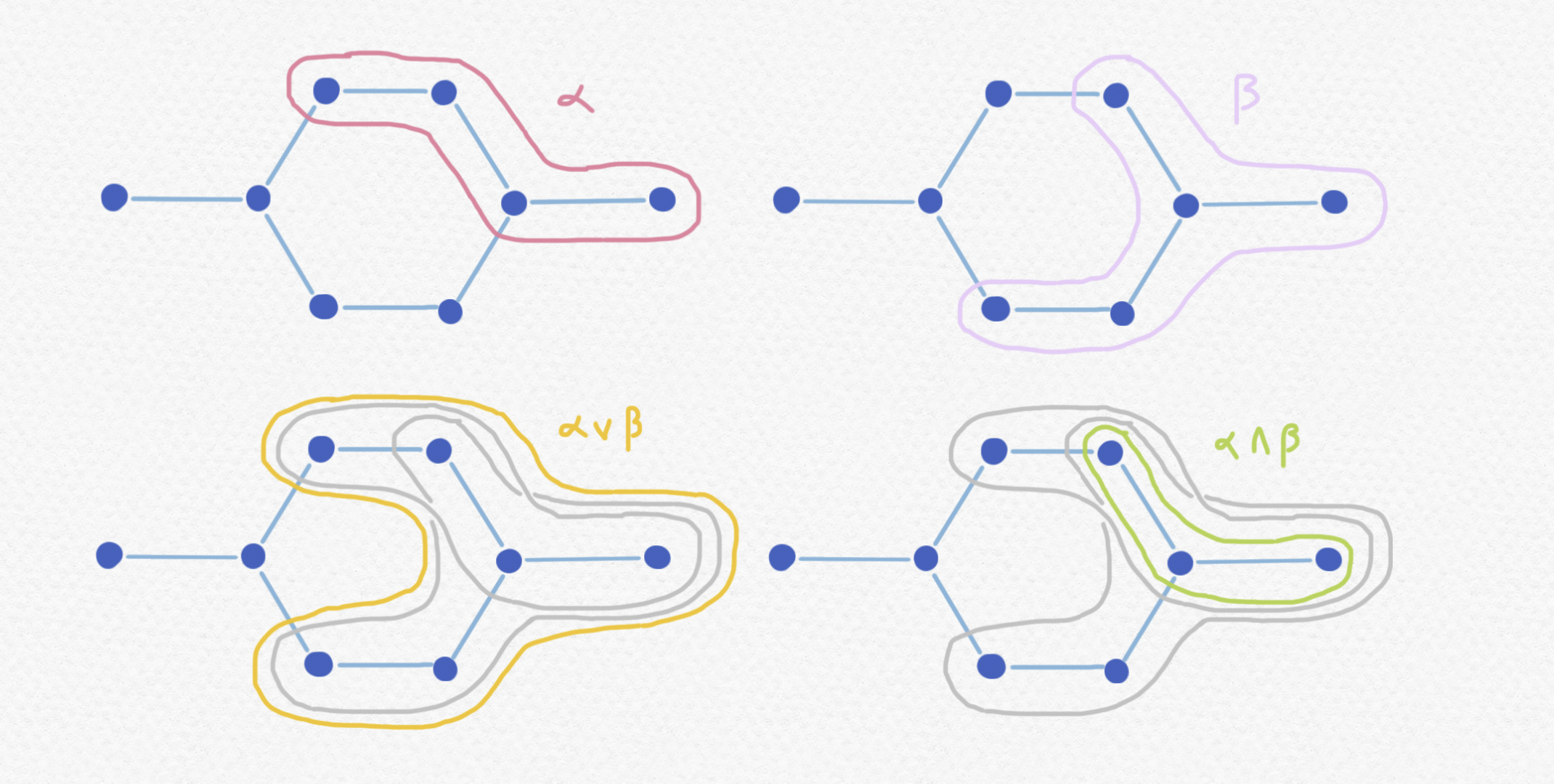
Definir implicación $\to$ y negación $\neg$ no es tan sencillo. El intento más ingenuo de definir el valor de verdad de $\neg\alpha$ sería como el conjunto de momentos en los cuales no es cierto $\alpha$, o sea el complemento del subconjunto $U\subset\mathbb P$. Pero si lo definimos así no hay garantía de que éste sea sección final:
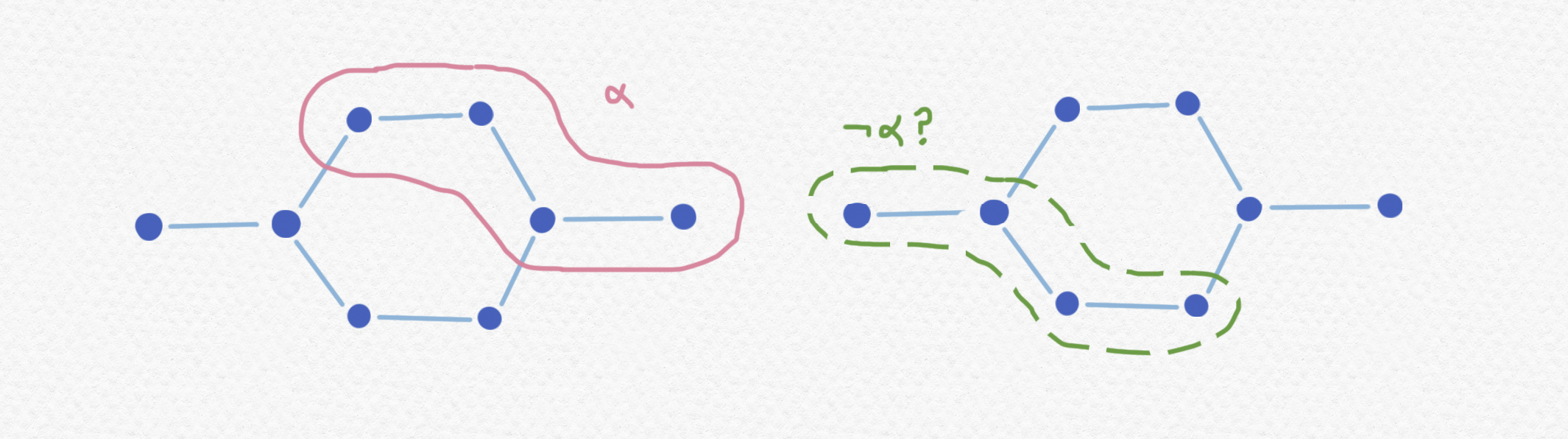
De hecho, podemos usar nuestro postulado de que lo cierto perdura por el tiempo para imponer restricciones en cuándo puede ser verdad la sentencia $\neg\alpha$. Si $\alpha$ está cierto en algún momento $t\in\mathbb P$ sabemos que $\neg\alpha$ no puede estar cierto en ningún instante que comparta un futuro con $t$, o sea si $\neg\alpha$ está cierto en $u\in\mathbb P$ entonces no debe existir ningún $v\in\mathbb P$ tal que $v\ge t$ y $v\ge u$. Pues si existiera sucedería que $\alpha$ y $\neg\alpha$ tendrían que estar ciertos simultáneamente en el momento $u$ y por supuestísimo que no queremos permitir que haya contradicción.
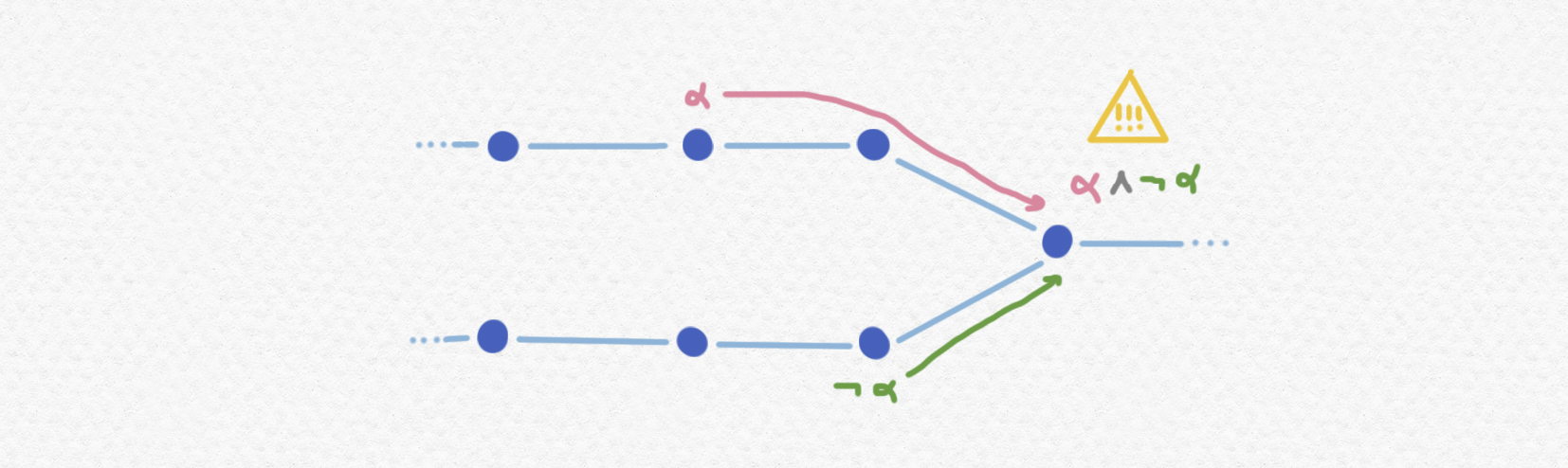
Teniendo en cuenta esa restricción ¿por qué no definir $\neg\alpha$ de la forma más liberal que no produce contradicción y dejar que el valor de verdad de $\neg\alpha$ sea simplemente el conjunto de elementos de $\mathbb P$ que no tienen futuro posible en el cual $\alpha$ sea verdad? Es decir, definimos el valor de verdad de $\neg\alpha$ así: Con esa definición el significado intuitivo de $\neg\alpha$ no se describe adecuadamente con "no $\alpha$" sino tal vez con "nunca $\alpha$" - una prueba de $\neg\alpha$ no sólo indica que $\alpha$ no es cierto en ese instante sino tampoco podrá llegar a ser cierto en ningún futuro posible a partir de ahora mismo. Nota que este conjunto sí será una sección final porque los momentos que quedan después de algún momento también quedan después de todos los que quedan antes de él (por la propiedad transitiva del orden parcial) así que si $\alpha$ no está cierto en ningún futuro de un momento ni estará cierto en el futuro de ningunos de sus momentos futuros. Aquí está un ejemplo de cómo se calcula el valor de verdad de $\neg\alpha$ desde lo de $\alpha$:
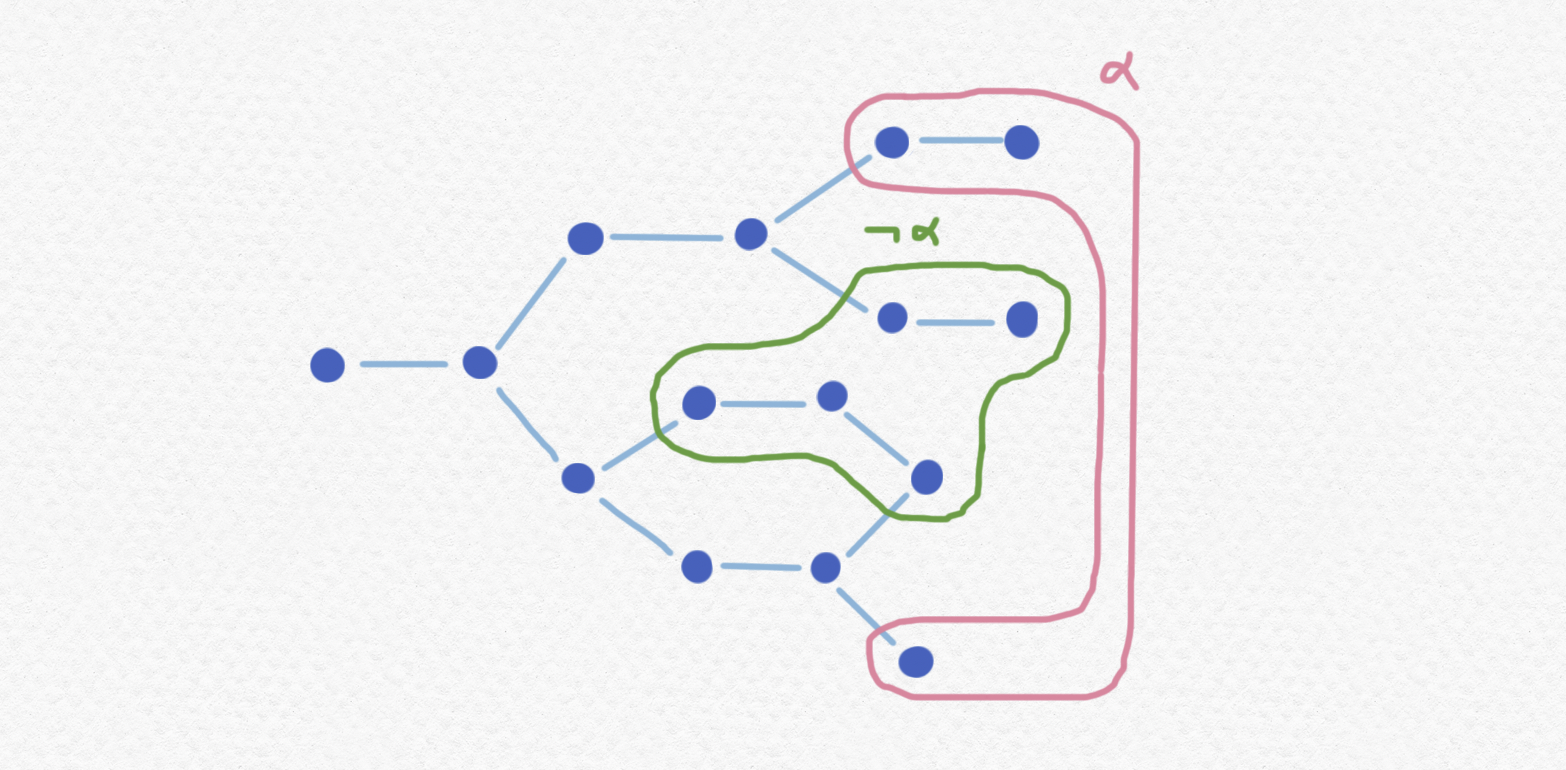
El valor de la implicación $\alpha\to\beta$ definimos con una construcción semejante. Diremos que $\alpha\to\beta$ es cierto en el momento $t\in\mathbb P$ si $\beta$ está cierto en todos los momentos en el futuro de $t$ en los cuales $\alpha$ está cierto. Intuitivamente será más apto referirnos a $\alpha\to\beta$ diciendo "$\beta$ tan pronto como $\alpha$" que "$\alpha$ implica $\beta$". Fíjate que si $\bot$ es una sentencia con valor de verdad igual al conjunto nulo entonces el valor de $\alpha\to\bot$ será lo mismo que $\neg\alpha$.
En la lógica clásica existen fórmulas que se llaman tautológicas como $\alpha\to\alpha$ y $\alpha\lor\neg\alpha$ que estarán ciertos independientemente del valor de verdad de $\alpha$. Podemos generalizar ese concepto a esta lógica temporal: decimos que una fórmula que depende de varias sentencias es tautológica si y sólo si estará cierto en todos los instantes de $\mathbb P$ de manera independiente de las sentencias involucradas. Nota que cuáles fórmulas son tautológicas dependerá del marco con el que trabajamos y ya veremos que no todos tienen los mismos tautologías.
Aquí está una lista de tautologías clásicas:
- $\alpha\lor\neg\alpha$ o sea la ley del tercio excluido
- $(\neg\alpha)\lor (\neg\neg\alpha)$
- $\neg(\alpha\land\neg\alpha)$ o sea el principio de no contradicción
- $\neg\neg\alpha\to\alpha$ o sea eliminación de la doble negación
- $\alpha\to\neg\neg\alpha$ o sea introducción de la doble negación
- $\neg(\alpha\land\beta)\to (\neg\alpha)\lor(\neg\beta)$
- $(\alpha\to\beta)\lor (\beta\to\alpha)$
Nota que el principio de no contradicción sigue siendo tautología en todos marcos, pues hemos definido $\neg\alpha$ con el propósito de no violar esa ley. La introducción de la doble negación también vale en todos marcos $\mathbb P$ porque $\neg\neg\alpha$ será cierto en todos momentos en los cuales $\alpha$ está cierto, pues si $\alpha$ está cierto perdurará hasta todos momentos futuros así que $\neg\alpha$ no podrá estar cierto durante ningunos de ellos. Pero fíjate que la ley de no contradicción no es tautológica en todos marcos. Por ejemplo, en el ejemplo que vimos antes:
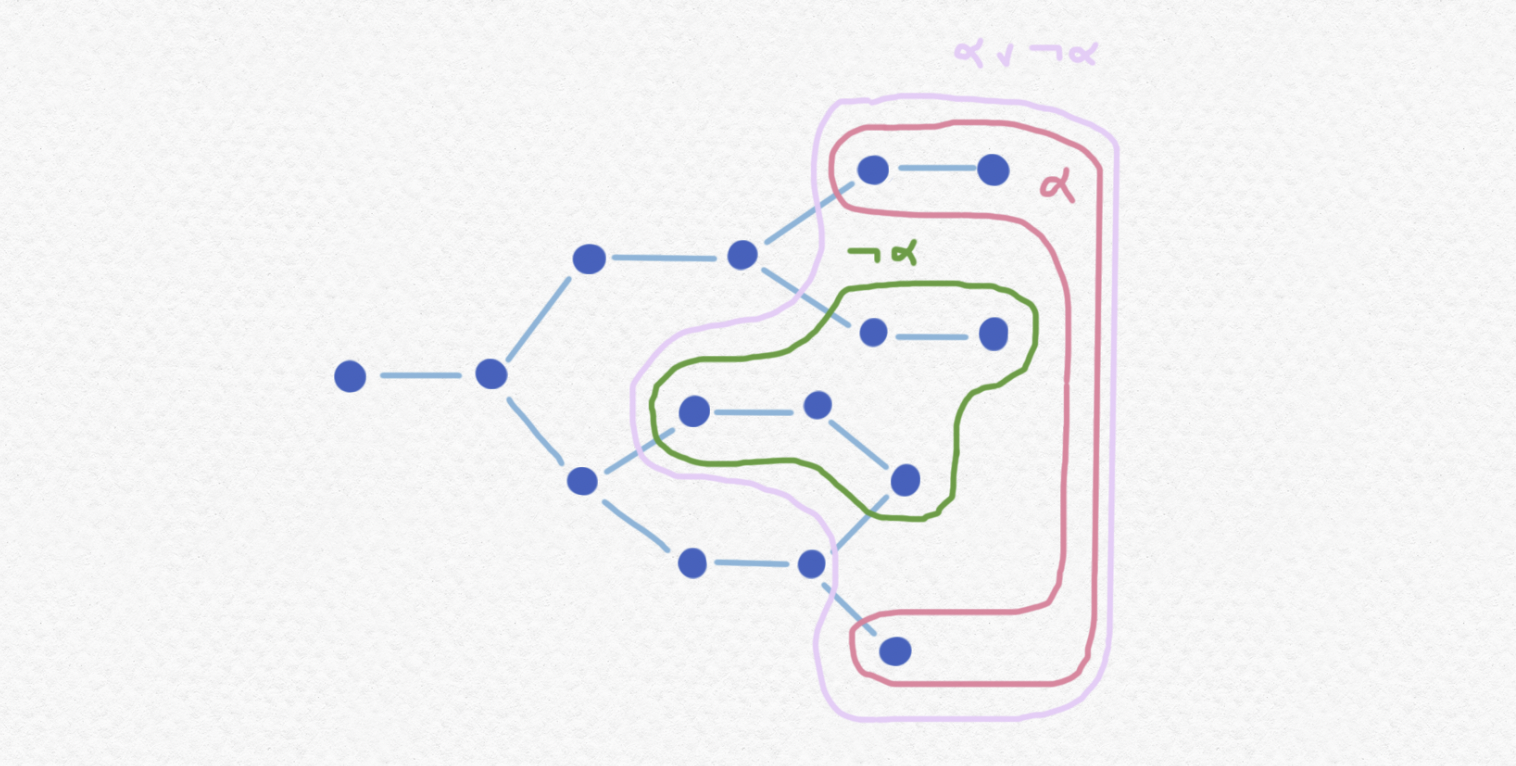
Ni necesitamos un marco $\mathbb P$ tan complejo. Tal vez el marco más sencillo que falta la ley del tercio excluido es el marco con dos elementos comparables. Éste tiene $3$ valores de verdad y lo siguiente no satisface la LTE:
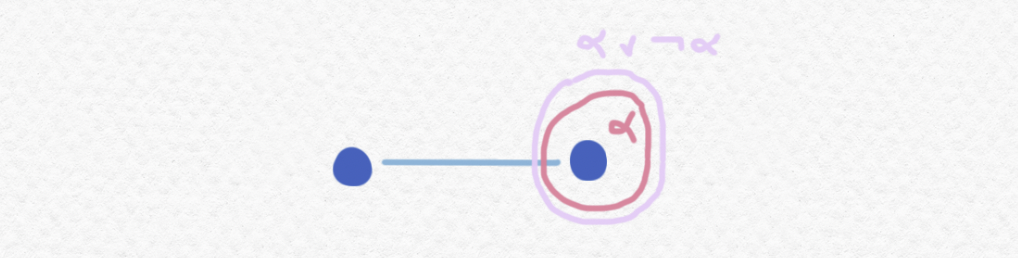
Pues en el primer instante de $\mathbb P$ no es cierto $\alpha$ pero estará cierto "más tarde" y por eso no se lo puede descartar, entonces ni está cierto $\neg\alpha$. Ni será la eliminación de la doble negación cierto en este marco, pues $\neg\neg\alpha$ está cierto en el primer momento (porque éste tiene un futuro en el que estará cierto $\alpha$) sin que $\alpha$ esté cierto en el mismo momento.
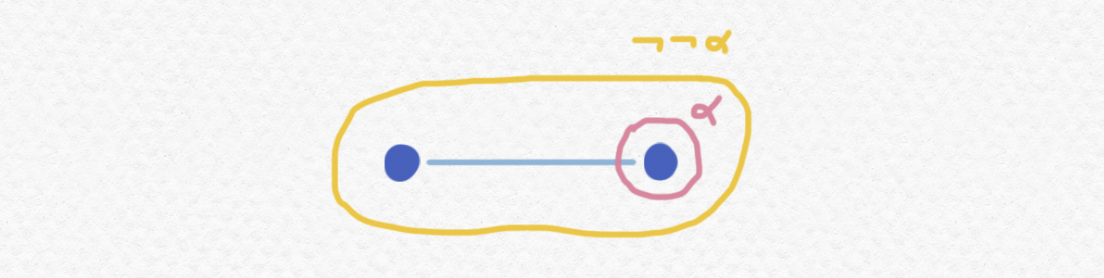
De hecho podemos deducir que en cualquier marco en el que existen $2$ elementos equiparables tendremos situaciones semejantes y entonces fallará la LTE tanto como la EDN. Pues hay varios marcos que no tienen dos elementos distintos y equiparables pero no son muy interesantes.
De hecho sí que hay algo significante que decir sobre esos casos "degenerados" en los que son válidos la LTE y la EDN. Si ningún par de elementos distintos de $\mathbb P$ es comparable entonces el marco parecerá una colección de puntos esparcida y cualquier subcolección de estos puntos constituirá una sección final, es decir que todos los $2^{|\mathbb P|}$ subconjuntos de $\mathbb P$ posibles serán valores de verdad. Las operaciones de $\land,\lor$ y $\neg$ en este caso se degeneran en las operaciones típicos de intersección, unión y complemento.
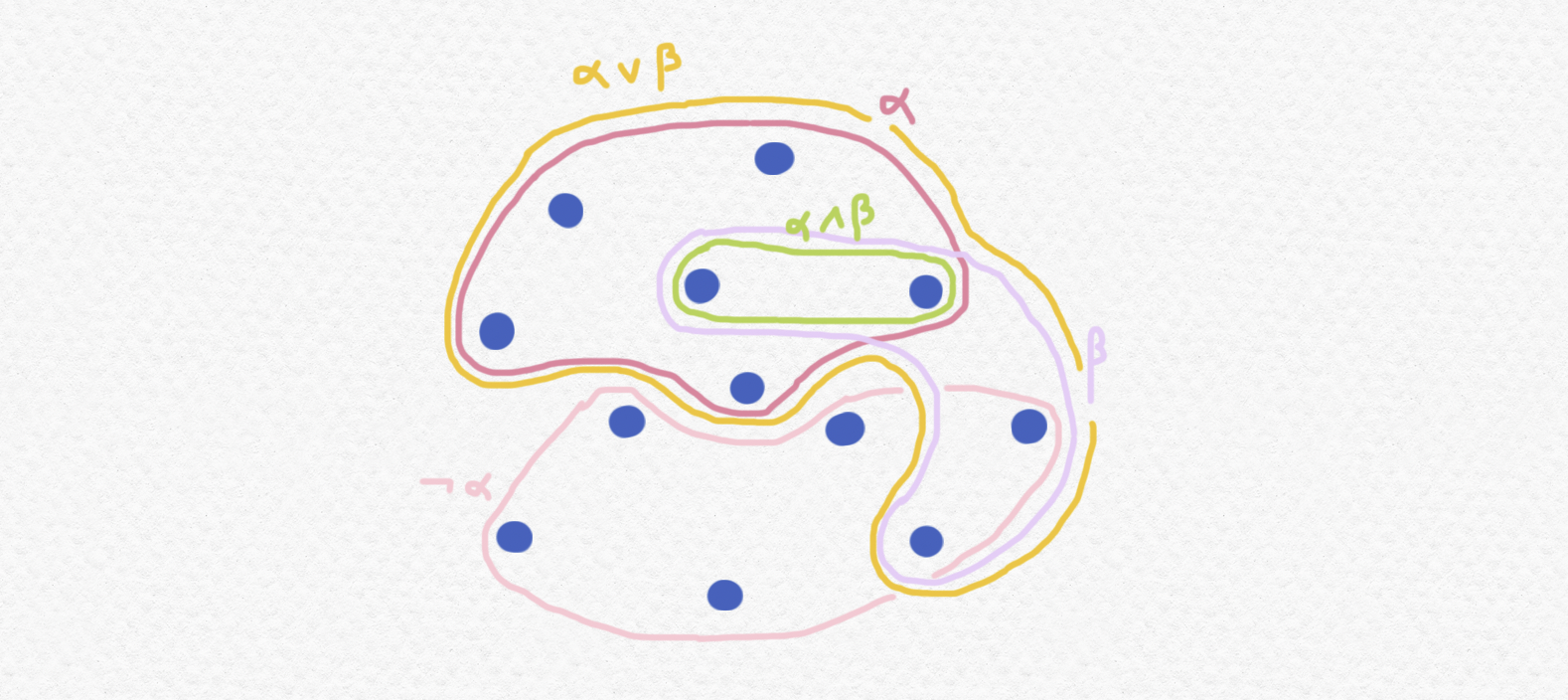
Si has estudiado la lógica o el teoría de conjuntos tal vez reconocerás esta estructura como una álgebra booleana que es un objeto algebraico que se puede definir abstractamente en términos de las identidades que satisfacen sus dos operaciones binarias $\land,\lor$, su única operación unaria $\neg$ y los elementos distinguidos $0$ y $1$. De hecho la estructura algebraica formada por los valores de verdad de una marco arbitrario (y no degenerado) es menos conocido pero también tiene nombre propio: un álgebra de Heyting, que se define como un retículo con operaciones de máximo $\lor$ y mínimo $\land$ y un elemento máximo y otro elemento mínimo, y finalmente otra operación binaria $\to$ que tiene la propiedad de que $(a\to b)\geq x$ si y sólo si $b\geq a\land x$, o sea $a\to b$ es el máximo de los elementos de la álgebra $H$ que cumplen $a\land x\leq b$. Toda álgebra de valores de verdad de un marco $\mathbb P$ constituye un álgebra de Heyting $H$ pero al lector le propongo la pregunta: ¿proviene cada álgebra de Heyting de la álgebra de valores de verdad de algún marco? Dado una álgebra de Heyting $H$ ¿puedes construir un marco $\mathbb P$ que da lugar a éste? (Te sugiero que primero consideras la misma pregunta con las álgebra booleanas que son más sencillas.)
Hay mucho que decir acerca de la relación entre el índole de un orden parcial de un marco $\mathbb P$ y las tautologías de su lógica. Por ejemplo, ya hemos notado que
$\alpha\lor\neg\alpha$ es tautológica si y sólo si $\mathbb P$ es trivial, o sea si ningún par de elementos es comparable.
¿Qué estructura tiene que poseer $\mathbb P$ para que $\neg\alpha\lor\neg\neg\alpha$ sea tautológica? ¿Qué tal $(\alpha\to\beta)\lor (\beta\to\alpha)$? Si $\mathrm{LTE}(\sigma)$ denota la sentencia $\sigma\lor\neg\sigma$ y $\mathrm{EDN}(\sigma)$ denota la sentencia $\neg\neg\sigma\to\sigma$ para cada sentencia $\sigma$, ya hemos visto que existen marcos en los cuales $\mathrm{LTE}(\alpha)$ no es tautológica - ¿puedes encontrar algunos en los cuales $\mathrm{LTE}(\mathrm{LTE}(\alpha))$ o $\mathrm{EDN}(\mathrm{EDN}(\alpha))$ no son tautologías? ¿Puedes encontrar un marco en el cual $\mathrm{LTE}(\alpha)$ no es tautológica pero $\mathrm{LTE}(\neg\alpha)$ sí?
Ya hemos visto que se complica mucho la lógica si consideramos marcos variados pero ¿para qué sirve si no vamos más allá para incorporarlos en teorías más amplias de las matemáticas que se basan en estas lógicas? Parece que lo más básico que querríamos para construir estructuras matemáticas interesantes sería una teoría de conjuntos. ¿Cómo funcionarían los conjuntos si trabajáramos con una de esas lógicas alternativas?
El intento actual más sobresaliente de generalizar la teoría de conjuntos a las lógicas más constructivas se lleva a cabo con herramientas de la teoría de categorías y un universo de objetos que "se comportan como conjuntos" se llama un topos. La definición formal de un topos lleva mucha jerga de la teoría de categorías:
Un topos $\mathscr E$ es una categoría que posee todos límites y colímites finitos, objetos exponenciales y un clasificador de subobjetos.
pero aquí está mi intento de describir informalmente los requisitos de ser un topos y sus homólogos en la categoría de conjuntos $\mathsf{Set}$ (que es un topos en sí). La existencia de "límites y colímites" corresponde aproximadamente a la existencia de uniones disjuntas y productos de familias arbitrarias de conjuntos tanto que cocientes de conjuntos por relaciones de equivalencia. Dado dos objetos $X,Y$ de la categoría, un "objeto exponencial" $Y^X$ juega el mismo papel que el conjunto de todos los funciones entre dos conjuntos en la categoría $\mathsf{Set}$. Finalmente el concepto de un "clasificador de subobjetos" es una generalización de la relación especial que existe en $\mathsf{Set}$ entre el conjunto potencia de un conjunto y el conjunto de funciones desde este conjunto hacia un conjunto con dos elementos. Es decir, hay una correspondencia entre los subconjuntos de un conjunto y sus "funciones características" que indican que si elemento del conjunto está presente en el subconjunto o no. Si has visto mi entrada anterior que trata de la teoría de tipos, vale conceptualizar un topos como un ambiente en el cual puedes hacer todas las mismas construcciones de sumas, productos, sumas y productos dependientes, tipos de funciones etc.
Bueno, pues no hay que entender lo que es un topos por lo general para juguetear con teorías de conjuntos alternativas. Hay una cierta familia de topoi que se denotan $\mathsf{Set}^{\mathbb P}$ cuyos objetos no son conjuntos sino conjuntos "que cambian a lo largo del tiempo" tal que "el tiempo" se representa otra vez con el marco $\mathbb P$. (Formalmente se define como una categoría de funtores por si acaso conoces esa construcción.) Los "conjuntos" con los cuales trabajamos si usamos el marco $\mathbb P$ no constan de un solo conjunto, sino un conjunto distinto para cada elemento de $\mathbb P$ además de una familia de funciones que indican cómo están relacionados entre si esos conjuntos. Así que para especificar un conjunto de $\mathsf{Set}^{\mathbb P}$ tenemos que proveer los datos siguientes:
La última condición tiene que ver con "coherencia", o sea, requiere que las funciones que describen "cómo cambia el conjunto a lo largo del tiempo" no tienen conflictos entre si: los cambios que ocurren entre la hora $t$ y la hora $v$ son precisamente los que ocurren entre $t$ y $u$ juntos con los que ocurren entre $u$ y $v$. Un "elemento" de un tal "conjunto" $X$ se puede definir como una colección de elementos $x_t$ de todos los conjuntos $X_t$ tal que $x_t\in X_t$ para cada $t\in\mathbb P$ y tal que ellos conformen a los cambios descritos por las funciones $f_{i,j}$, o sea, que $f_{t,u}(x_t) = x_u$ para cada $t,u\in \mathbb P$.
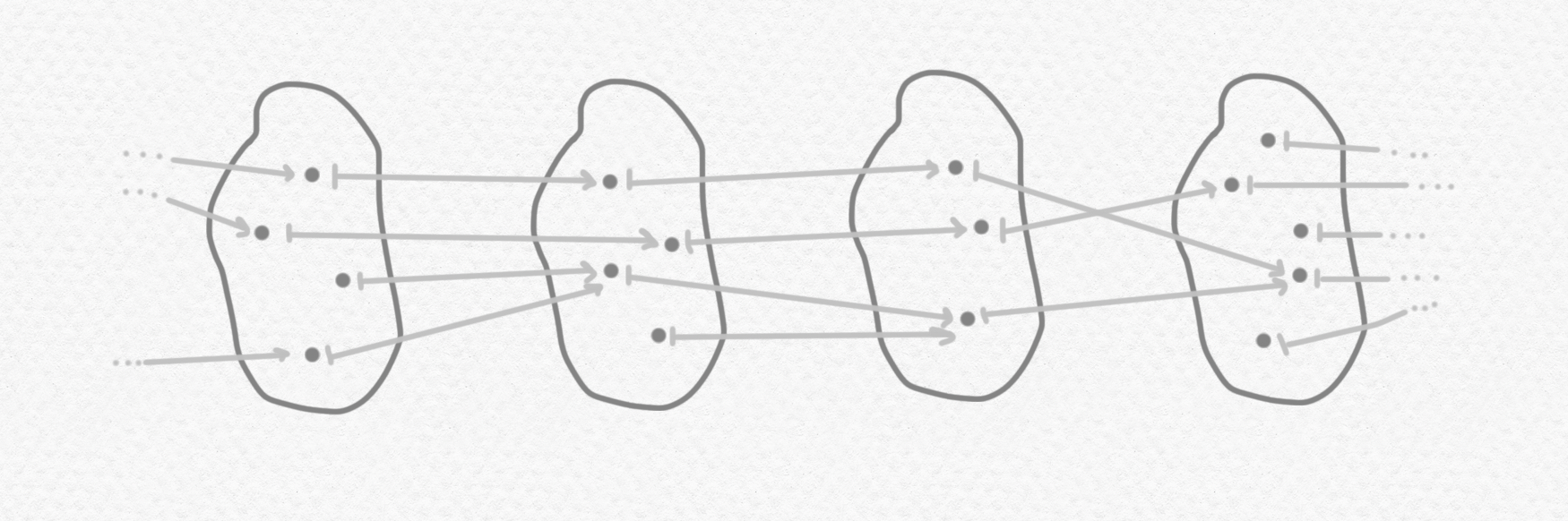
Aquí están dos elementos de este "conjunto":
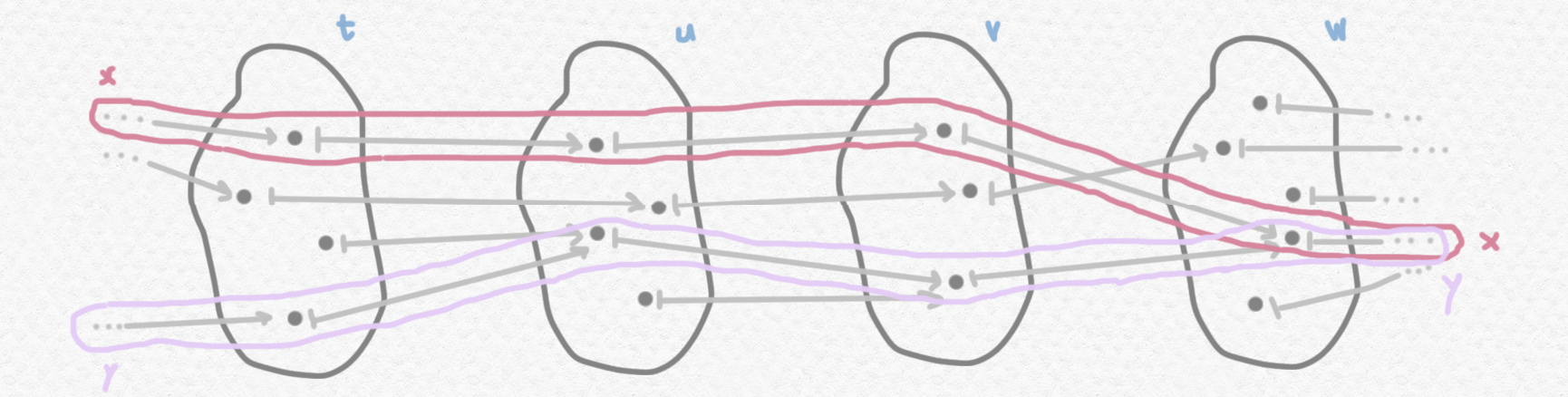
La manera obvia de definir igualdad de elementos sería dictaminar que la sentencia $(x = y)$ sea cierto si y sólo si los elementos de $X_t$ correspondientes a $x$ y $y$ son iguales en cada momento $t$, o sea si $x_t=y_t$ para cada $t\in\mathbb P$. Fíjate que si lo definimos así, entonces en el diagrama anterior la sentencia $(x=y)$ no es cierto pero la sentencia $\neg\neg(x=y)$ sí es cierto porque aunque $x_t=y_t$ no es verdad para cada $t\in\mathbb P$, sí queda cada momento antes de un futuro en el cual llegan a ser iguales.
Cosas aún más raras pueden pasar con estos "conjuntos temporales". Consideramos el ejemplo que sigue:
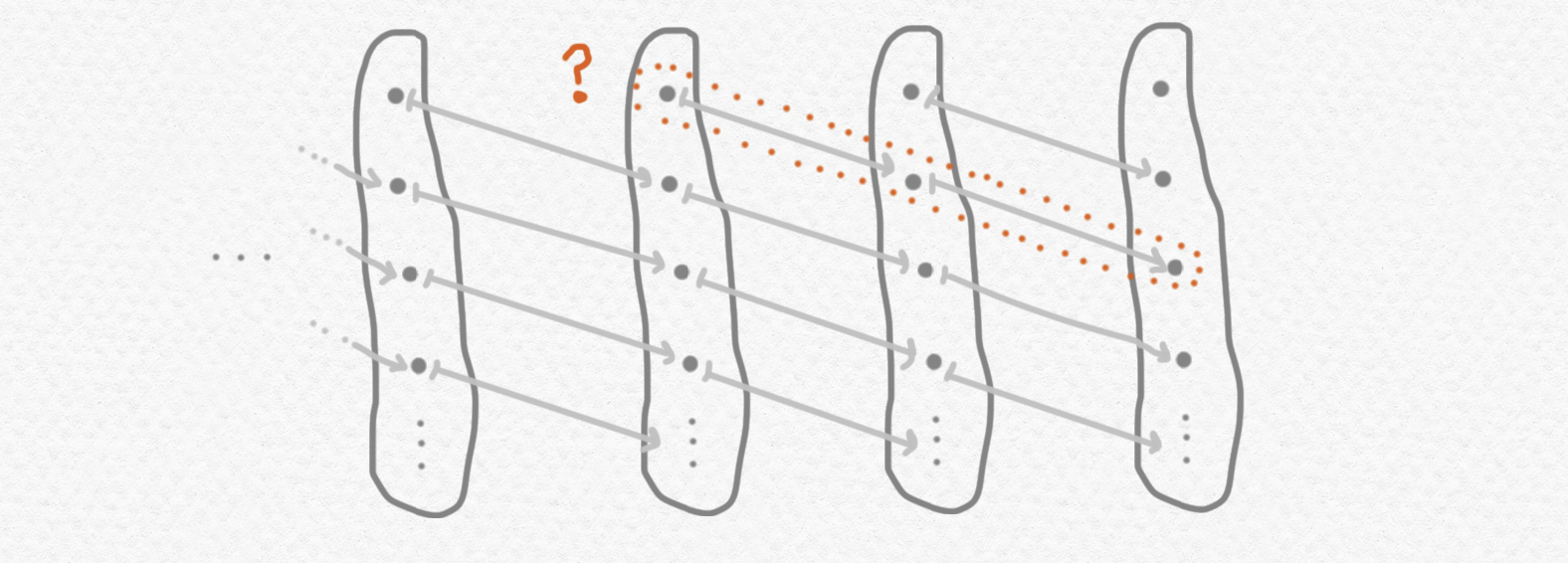
Fíjate que este conjunto no tiene elementos ningunos. Pues si eliges un elemento $x_t$ de uno de estos conjuntos $X_t$ siempre existe un conjunto anterior $X_s$ con $s<t$ tal que $x_t$ no tiene ningún preimagen en $X_s$ y entonces no puede formar parte de un elemento de $X_t$. Pero claro que no diríamos nunca que este conjunto sea vacío... Aquí está otro ejemplo:
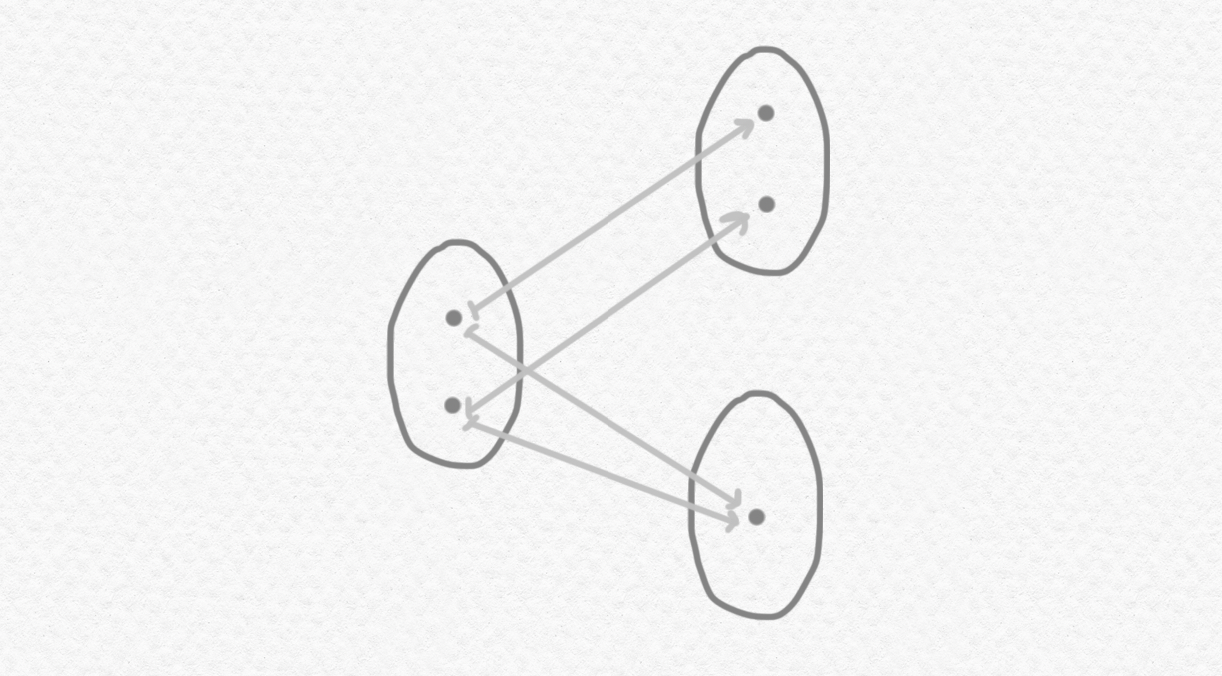
Este conjunto tiene $2$ elementos $x,y$ (¿puedes ver los dos elementos?) pero ni es cierto $(x=y)$ ni $\neg(x=y)$ ni $\neg\neg (x=y)$ ni $\mathrm{LTE}(x=y)$. Aquí se acaba la entrada pero como si quieres juguetear un poco más con estos conjuntos estrafalarios propongo que consideras los rompecabezas siguientes: