(Psst! Don't want to read this in Spanish? Here's a translation.)
En el lenguaje Scheme hay una particularidad muy interesante de ciertas estructuras de control. Cuando realizamos una llamada a función como (f x y) (en este caso una función con dos argumentos) se evalúa ambos argumentos x y y primero para entonces pasarlos a la función f. Podemos demostrar este fenómeno sintetizando argumentos que producen efectos secundarios una vez que son evaluados:
> (define x '(begin (display "evaluating x\n") 34))
> (define y '(begin (display "evaluating y\n") 35))
> (define (f a b) (+ a b))
> (eval x)
evaluating x
34
> (eval y)
evaluating y
35
> (f (eval x) (eval y))
evaluating x
evaluating y
69
Pero algunas estructuras de control que parecen funciones realmente no lo son por no tramitar sus argumentos así. Por ejemplo fíjate qué pasa cuando realizamos operaciones booleanas con la construcción and:
> (define x '(begin (display "evaluating x\n") #t))
> (define y '(begin (display "evaluating y\n") #f))
> (and (eval x) (eval y))
evaluating x
evaluating y
#f
> (and (eval y) (eval x))
evaluating y
#f
En concreto una invocación a and se va evaluando los argumentos uno tras otro hasta encontrar uno falso y devolver #f si lo encuentra o #t si no lo encuentra. Pues una vez que encuentra un argumento con el valor #f realmente no hay necesidad de evaluar el resto de los argumentos porque una vez que aparece un valor falso ya está determinado el resultado de la operación booleana. La construcción or emplea un truco semejante: una vez que encuentra el valor #t en sus argumentos entonces devuelve #t sin evaluar el resto.
Pues no suele influir esta peculiaridad mucho en el rendimiento de nuestros programas pero sí puede importar mucho en el caso de que una de las expresiones que se pasa como argumento produce error o entra en un bucle infinito de tal manera que no devuelve un valor válido. No nos cuesta mucho encontrar ejemplos de expresiones cuya evaluación nunca termina. Por ejemplo, si definimos (define btm '(eval btm) y entonces ejecutamos (eval btm) ya entramos en un bucle sin fin. Si intentamos pasar esta expresión chunga como argumento a una función nunca se acabará la ejecución aún si el resultado realmente no depende del valor del argumento. Por ejemplo la función (lambda x 0) en principio debe devolver 0 siempre pero cuando intentamos realizar la llamada ((lambda x 0) (eval btm)) nunca devuelve ningún valor por intentar evaluar btm. Por otro lado:
> (and #f (eval btm))
#f
pues debido a su tratamiento especial de argumentos and nunca intenta evaluar btm por eso logra devolver un valor. Por otro lado, la llamada (and (eval btm) #f) nunca termina porque intenta evaluar el primer argumento antes del segundo y la llamada (and #t (eval btm)) nunca termina porque el resultado de la expresión depende del valor del segundo argumento.
Pero diría que son muy distintos las evaluaciones (and (eval btm) #f) y (and #t (eval btm)). En el segundo caso realmente no tendría sentido asignarle un valor porque podría resultar o cierto o falso dependiendo del valor de (eval btm) y como éste no produce ningún valor booleano no hay manera de elegir un valor de esta expresión que no sea arbitraria. Por otro lado la intuición nos dice que la expresión (and (eval btm) #f) "debe" evaluar a falso, pues aunque el primer argumento no devuelve ningún booleano, si lo devolviera entonces la expresión resultaría falso en cualquier caso. De hecho podemos definir una versión propia de and que evalúa el segundo argumento antes del primero:
(define-syntax and2
(syntax-rules ()
((and2 x y)
(let ((tmp y))
(if tmp x #f)))))
Con esta construcción nos va (and2 (eval btm) #f) pero (and2 #f (eval btm)) no va - entonces tiene la misma debilidad and2 que and pero al revés. ¿Cómo podríamos escribir una estructura de control que evalúa las expresiones booleanas en todos casos que el resultado sea determinado por los argumentos que devuelven un valor?
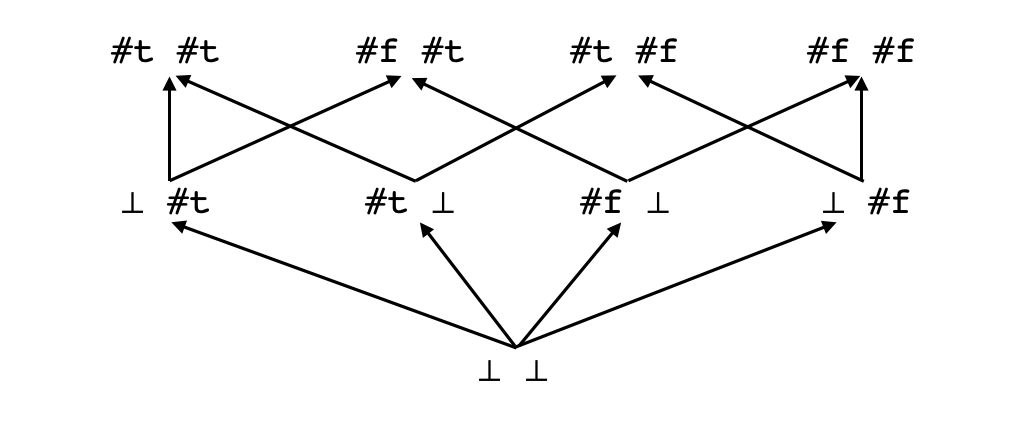
Voy a intentar describir más precisamente qué quiero decir aquí. Suponemos que hay una función (no de Scheme sino una función matemática que queremos implementar en Scheme) con varios argumentos: Para representar la posibilidad de pasar argumentos no bien definidos podemos ampliar el dominio de la función así: o sea que añadimos a cada componente del dominio y al rango un "valor" adicional $\bot$ que representa algo que no se puede evaluar o que no tiene valor definido. (Juro que yo no soy él que inventó esta notación rara.) Vamos a definir un orden parcial en el dominio de la función ampliada $\tilde f$ de la manera siguiente: diremos que una tupla $t=(a_1,\cdots,a_n)$ es "menor" que la tupla $t'=(a_1',\cdots,a_n')$ o sea $t\leq t'$ si y sólo si $t$ "podría ser igual a $t'$" si algunos de sus elementos no definidos (iguales a $\bot$) fueran definidos. Dicho más rigurosamente diremos que $t\leq t'$ si $a_i\ne a_i'$ sólo cuando $a_i = \bot$. Por ejemplo decimos que $(1,\bot,3)\leq (1,2,3)$. Intuitivamente si nos ponemos a evaluar los argumentos de una función y en algún instante resulta que el primer argumento se ha evaluado a $1$ y el tercer argumento a $3$ pero el segundo argumento sigue evaluándose, todavía es posible que salga un $2$ y que la sucesión de argumentos resulte $(1,2,3)$ al final. Por otro lado $(1,\bot,3)\nleq (1,2,4)$ pues como el tercer argumento se ha evaluado a $3$ ya no es posible que sea un $4$. En Scheme en concreto tendríamos el orden parcial siguiente para un par de argumentos booleanos:

en la cual figura $\bot$ representa el "valor" de una expresión como (eval btm).
Exigimos algunas propiedades de esta función $\tilde f$ para que quepa con nuestra intuición de la computación que representa. Lo primero es que mientras mejor definida sea la entrada a la función, mejor definido será la salida. Si $t'$ es una "evaluación posible" de $t$ o sea si $t\leq t'$, entonces $\tilde f(t')$ debe de ser una evaluación posible de $\tilde f(t)$ o sea $\tilde f(t)\leq \tilde f(t')$. Entonces exigimos la propiedad de monotonicidad: En particular si los argumentos $t$ bastan para determinar el valor de $\tilde f(t)$ y si $t'$ es "aún más específico" que $t$ entonces $\tilde f(t')$ tendrá que tener el mismo valor. Además si queremos considerar $\tilde f$ como una implementación de $f$ debe tener los mismos valores que $f$ en el subconjunto $A_1\times\cdots\times A_n$ de su dominio o sea cuando todos sus argumentos son bien definidos. Con el dibujo anterior del orden parcial en pares de booleanos en Scheme podemos visualizar el suborden de argumentos en el cual la implementación de and está definido y el suborden en el cual la operación lógica podría ser definida:
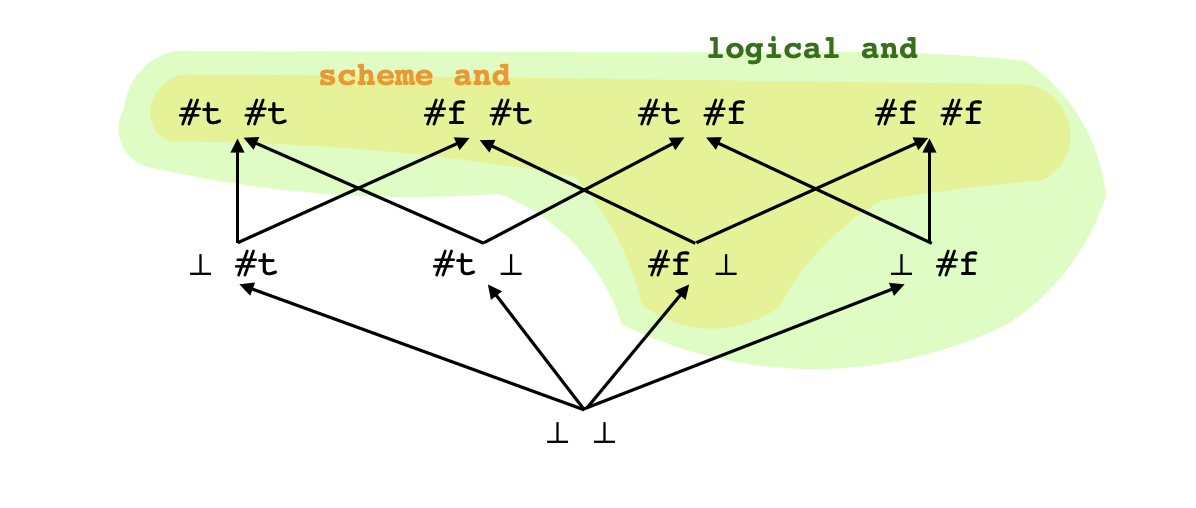
La mejor implementación de $f$ respeto a su robustez frente a argumentos mal formados sería una que le asigna un valor bien definido a cada conjunto de argumentos cuyos valores bien definidos determinan únicamente. Es decir, una implementación óptima de la conjunción lógica en Scheme devolvería un valor para cada par de argumentos dentro de la región verde. Puedes formular esta propiedad matemáticamente?
Pues basta ya con la formalización matemática. Tal vez la trato con más detalle en una entrada a continuación pero si te interesa leer más acera de la formalización de computaciones parciales debes leer sobre la teoría de dominios. Es un tema del cual quiero aprender más yo mismo.
De todos modos mi intento de implementar la operación de conjunción lógica de manera más robusta a las computaciones que no terminan involucra las hebras. Si evaluamos los argumentos uno tras otro entonces siempre quedará un caso en el cual espera el resultado de una computación que nunca termina mientras que el otro argumento determina completamente el resultado. Por otro lado si nos vamos evaluando los dos argumentos simultáneamente o sea evaluando cada uno poco a poco entonces podemos terminar la computación tan pronto como la llegada de un valor que determina el valor de la operación. Aquí está mi código:
(define-syntax andp
(syntax-rules ()
((andp x y)
(let* ((ch (make-channel))
(th1 (thread (lambda () (channel-put ch x))))
(th2 (thread (lambda () (channel-put ch y)))))
(and (channel-get ch) (channel-get ch))))))
Lo que cumple esta función es que crea un canal y entonces crean dos hebras th1 y th2 que comunican con el proceso padre a través del canal. Según la documentación de Racket acerca del paralelismo la llamada channel-get se bloquea hasta que un emisor envía un valor por el canal proporcionado y entonces devuelve éste. Así que al usar (and (channel-get ch) (channel-get ch)) cogemos como el primer argumento a and el valor de la computación que devuelve un resultado primero. Si este valor es falso entonces devuelve and el valor #f sin esperar otro valor con la segunda llamada a channel-get. Si probamos el funcionamiento de nuestra implementación andp observamos los resultados siguientes:
> (andp #f (eval btm))
#f
> (andp (eval btm) #f)
#f
Pues no sé si sería factible usar esta operación en la práctica. La creación de hebras debe generar muchos gastos así que creo que un programa que usa la implementación paralela para cada conjunción lógica sería muy ineficiente. Sin embargo podrían surgir casos en los cuales vale la pena, en concreto en computaciones en las cuales es probable que una parte tarde mucho más que otra en evaluarse.
También podemos considerar el manejo de expresiones sin evaluación por funciones más compleja que las operaciones booleanas. Por ejemplo considera la estructura de control if que también tiene un flujo de control especial en Scheme. Durante la evaluación de la expresión (if t x y) se evalúa t primero y si resulta cierto entonces devuelve el valor de x y si resulta falso devuelve el valor de y de manera que sólo computa el valor o de x o de y. Por ejemplo las computaciones (if #t 23 (eval btm)) y (if #f (eval btm) 23) sí devuelven un valor (ambos evalúan a 23). Si el primer argumento t no se puede evaluar entonces ni se evalúa (if t x y) pero fíjate que hay casos en los cuales el resultado no depende del valor de t. Por ejemplo en la expresión (if (eval btm) 23 23) realmente no hay necesidad de evaluar (eval btm) porque ya sea el valor del primer argumento #t o #f el resultado final será 23. Para implementar la estructura if-else con mejor manejo de este caso especial también podemos utilizar las hebras:
(define-syntax ifp
(syntax-rules ()
((ifp test x y)
(let* ((ch (make-channel))
(th1 (thread (lambda () (if (eqv? x y) (channel-put ch x) 0))))
(th2 (thread (lambda () (if test x y)))))
(channel-get ch)))))
Con esta implementación conseguimos los resultados siguientes:
> (ifp #t 23 (eval btm))
23
> (ifp #f (eval btm) 23)
23
> (ifp (eval btm) 23 23)
23
mientras que evaluaciones como (if (eval btm) 23 24) y (if #t (eval btm) 23) todavía serán sin fin, pues sus resultados dependerían de la computación infinita de (eval btm).
Echamos un vistazo brevemente a un ejemplo más complejo que trata de la implementación de una función que compara dos listas y decide si son iguales o no. Aquí están dos implementaciones no paralelas:
(define (comp-list-1 l1 l2)
(cond ((empty? l1) (empty? l2))
((empty? l2) #f)
(else (and (eqv? (eval (car l1)) (eval (car l2)))
(comp-list-1 (cdr l1) (cdr l2))))))
(define (comp-list-2 l1 l2)
(cond ((empty? l1) (empty? l2))
((empty? l2) #f)
(else (and (comp-list-2 (cdr l1) (cdr l2))
(eqv? (eval (car l1)) (eval (car l2)))))))
Para los argumentos que se portan bien estas dos implementaciones proporcionarán los mismos resultados pero son muy distinto en cuanto a su tratamiento de listas que contienen entradas que no se puede evaluar. Por ejemplo como comp-list-1 compara las dos listas de principio hacia el final es capaz de distinguir entre las dos listas '(1 (eval btm)) y '(2 3) porque detecta la diferencia entre 1 y 2. No es capaz de distinguir entre '(1 (eval btm) 3) y '(1 2 4) porque se topa con una entrada sin evaluación antes de encontrar las entradas 3 y 4 que le permitirían distinguir entre las dos listas. El asunto es al revés para comp-list-2. De hecho podemos clasificar explícitamente los pares de listas entre las cuales son capaces de distinguir las dos implementaciones. En concreto (comp-list-1 l1 l2) devuelve un resultado si:
l1 ni l2 tiene elementos sin evaluaciónl1 y l2 son distintos y la primera entrada en la cual no son iguales tiene evaluación en ambas listasPor otro lado (comp-list-2 l1 l2) devuelve un resultado si:
l1 ni l2 tiene elementos sin evaluaciónl1 y l2 son distintas y la última entrada en la cual no son iguales tiene evaluación en ambas listasUna particularidad interesante es que comp-list-2 detecta desigualdad entre dos listas con largos distintos sin intentar evaluar ni un elemento. Pero además de comp-list-1 y comp-list-2 podemos diseñar una implementación paralela (y poco eficiente) que aprovecha de nuestra construcción anterior andp:
(define (comp-list-p l1 l2)
(if (empty? l1)
(empty? l2)
(andp (eqv? (eval (car l1)) (eval (car l2)))
(comp-list-p (cdr l1) (cdr l2)))))
Con esta implementación las condiciones de terminación son mucho más flojas. En concreto sólo es necesario que las dos listas tienen largos distintos o que tienen dos entradas correspondientes desiguales en cualquiera posición con evaluación. Esta implementación es capaz de distinguir tanto entre '(1 (eval btm)) y '(2 3) como entre '(1 (eval btm) 3) y '(1 2 4). Además puede distinguir entre las listas '((eval btm) 34 (eval btm)) y '((eval btm) 35 (eval btm)) entre las cuales ni comp-list-1 ni comp-list-2 es capaz de distinguir.