En esta entrada pretendo presentar tres ejemplos de mónadas que además de ser interesantes en sí me han ayudado a intuir mejor lo que es una mónada, un esfuerzo que (como muchas cosas en la teoría de categorías) casi siempre va mejor considerando ejemplos concretos. Para esta entrada no hace falta saber de memoria ninguna definición de la teoría de categorías, pero ayudaría tener alguna concepción de lo que es un funtor y lo que es una mónada, tal vez por haber visto otros ejemplos antes ya sean de las matemáticas o de la programación.
Para rellenar los detalles rigurosos que no he tratado en esta entrada, aquí están algunos conceptos de la teoría de categorías que se debe conocer:
En cada uno de mis ejemplos hay varios pasos que rellenar para establecer que las construcciones descritas realmente son mónadas, como por ejemplo:
Así que, si conoces la teoría de categorías y te interesa explorar estos ejemplos de una manera más formal, te sugiero que intentes definir precisamente las mónadas siguientes (en $\mathsf{Set}$, digamos) para comprobar rigurosamente que son mónadas. Yo por mi parte me gustaría hacerlo también al final, pero no puedo negar que parece un ejercicio bastante exigente por tener tantos detalles que vigilar. Como referencia general para el estudio de la teoría de categorías, yo recomendaría el libro Categories for the Working Mathematician (es la que uso yo personalmente).
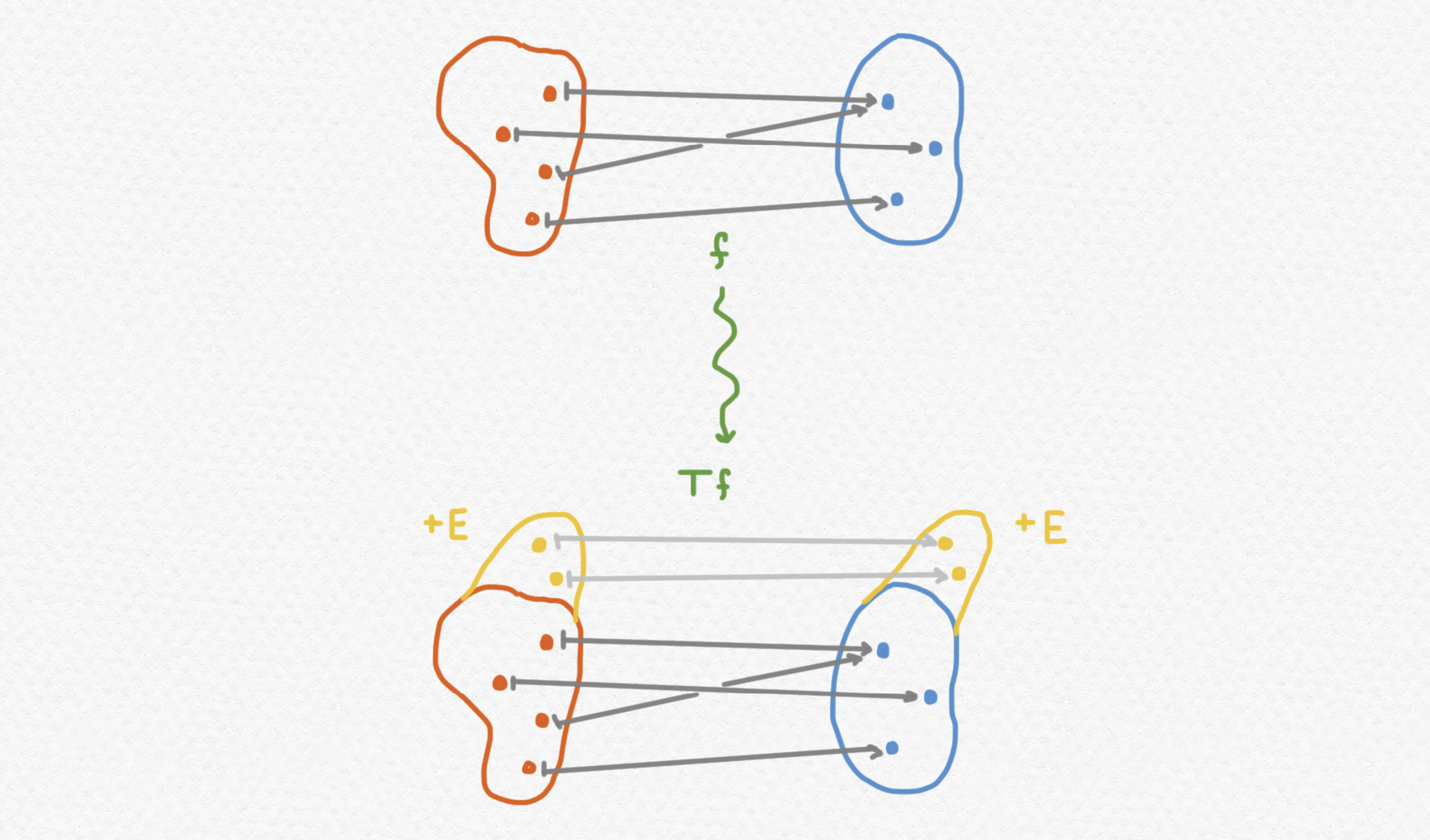
En una categoría $\mathsf C$ que posee coproductos, dado un objeto fijo $E$ de $\mathsf C$, se puede definir una mónada $T:\mathsf C \to \mathsf C$ que lleva $A\mapsto A+E$ para cada objeto $A$ de $\mathsf C$, y $f\mapsto i_B\circ f + i_E$ para cada flecha $f:A\to B$ de la categoría, donde $i_B:B\to B+E$ y $i_E:E\to B+E$ son las inclusiones en el coproducto. Este funtor (como muchos) es más fácil de conceptualizar en la categoría de conjuntos $\mathsf{Set}$: a cada conjunto le agrega una copia del conjunto fijo $E$ y para cada aplicación $f$ se le extiende a un morfismo $Tf$ que se comporta como la aplicación original en el componente preexistente de su dominio per que se comporta como la identidad en el componente nuevamente pegado al dominio y al codominio.

Verificar que esta construcción aún produce un funtor, o sea que $T:\mathsf C \to \mathsf C$ cumple $T(g\circ f) = Tg\circ Tf$ y así preserva la composición, no es muy difícil en $\mathsf{Set}$ pero es un poco más complejo en una categoría arbitraria con coproductos. Como quiero enfocarme en el aspecto intuitivo en esta entrada no hago una demostración, pero se lo puede demostrar como un ejercicio utilizando la propiedad universal que se usa para definir el coproducto y considerando el diagrama siguiente:
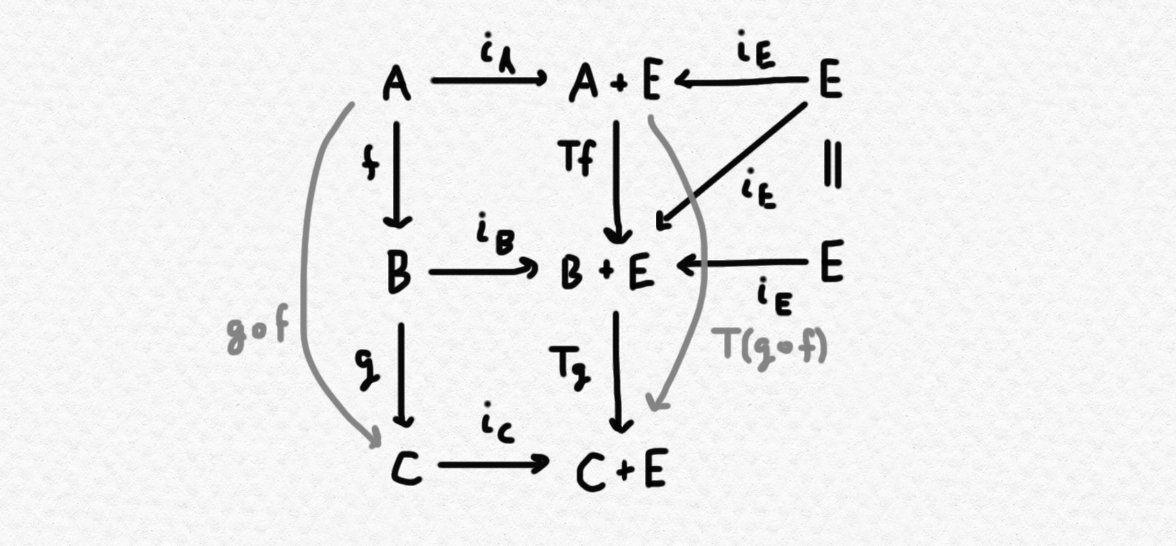
Para definir $T$ como una mónada todavía hace falta proporcionar la unidad $\eta: 1_\mathsf{C}\Rightarrow T$ y la multiplicación $\mu:T^2\Rightarrow T$. La unidad "embebe" un objeto $A$ en $A+E$ usando la inclusión del coproducto, o sea $\eta_A = i_A$ - en $\mathsf{Set}$ por ejemplo, la unidad $\eta_A:A\to E$ es una simple inclusión de $A$ en la unión disjunta $A+E$.
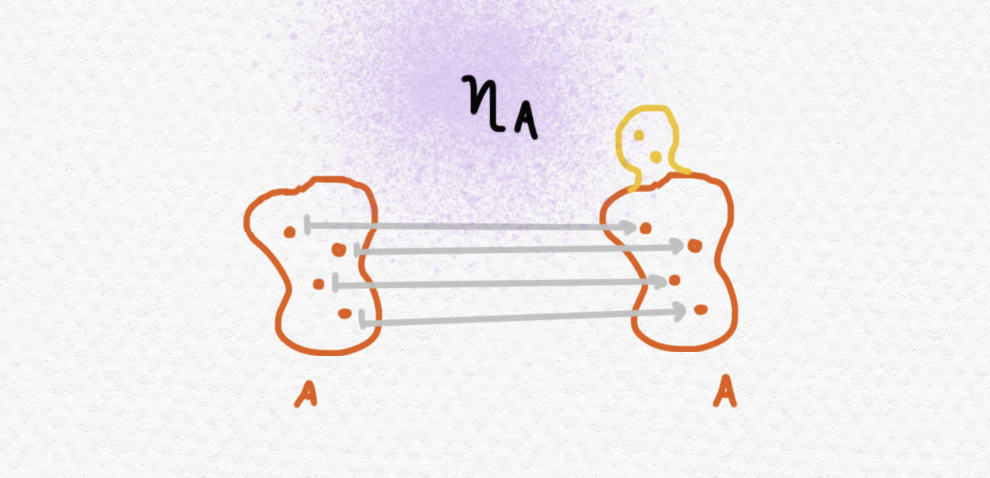
La multiplicación $\mu$ es un poco más interesante. Si el objeto $(A+E)+E$ consiste en $A$ con $E$ dos veces agregado, el componente de la multiplicación en $A$, o sea $\mu_A:(A+E)+E\to A+E$ "colapsa" las dos copias de $E$ en una sola.
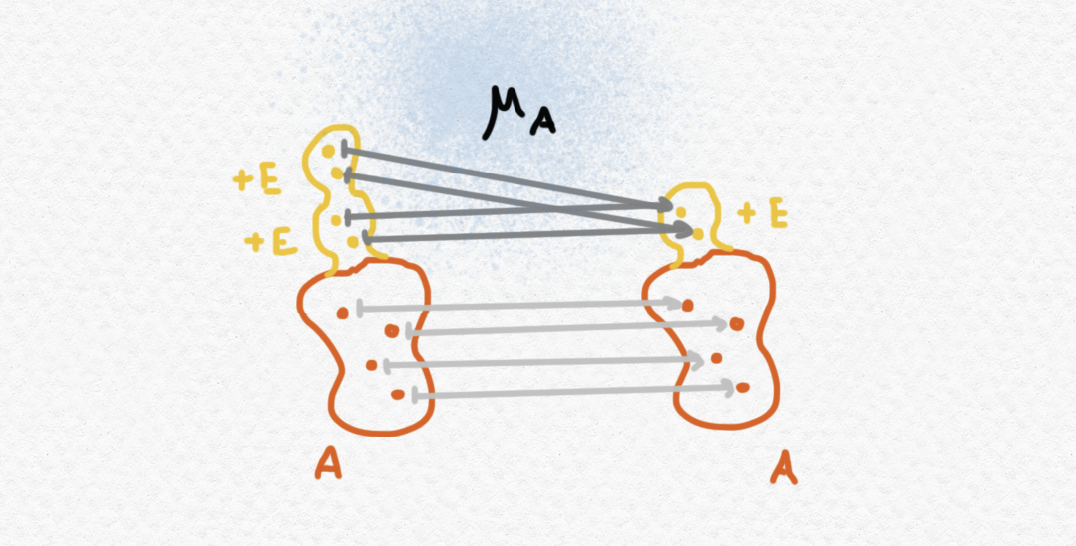
Formalmente podemos definir la multiplicación escribiendo $\mu_A = \mathrm{id}_{A+E} + i_E$.
Ahora, ¿qué hace esta mónada intuitivamente? En el contexto de la programación y la teoría de tipos mi me gusta pensarla como un funtor que le proporciona a cada aplicación una colección de valores "excepcionales" que están disponibles para cada aplicación. Si un morfismo $f:A\to B$ representa una aplicación que transforma cada elemento de $A$ en un elemento de $B$, entonces un morfismo $f:A\to TB$ representa una aplicación que transforma cada elemento de $A$ opcionalmente en un elemento de $B$, o bien en un elemento de $E$ si no. Existen varias interpretaciones de este tipo de comportamiento en la programación: $E$ podría contener valores no definidos como undefined o null, un valor que produce una computación que no termina, o una computación que termina produciendo un error. Así que, si $E$ representa alguna colección de "resultados obstinados" de los cuales no se puede recuperar (errores, excepciones, no terminación etcétera) los morfismos de la categoría Kliesli $\mathsf{C}_T$ representarían aplicaciones que no tienen que ser totalmente definidas en sus dominios respectivos sino que pueden producir estos valores excepcionales para algunas (o todas) las entradas.
Por ejemplo, suponemos que $\mathsf{C}$ es una categoría de los tipos y las aplicaciones que se puede definir en algún lenguaje de programación y que queremos ampliar el lenguaje habilitando funciones parciales con algunos valores sin definir y agregando nuevos tipos que involucran números de coma flotante que pueden dar lugar a excepciones de coma flotante. Entonces podríamos considerar donde $\mathtt{undef}$ representa un valor no definido y $\mathtt{fpe}$ representa una excepción de coma flotante. La categoría Kliesli $\mathsf{C}_T$ contiene aplicaciones que le corresponden a las aplicaciones de la categoría original $\mathsf{C}$, en concreto las aplicaciones que no producen los valores $\mathtt{undef}$ y $\mathtt{fpe}$ excepto cuando los reciben como entrada, pero además contiene un abanico más amplio de aplicaciones que a veces producen valores de su codominio y a veces producen valores "malos" de $E$.
Si interpretamos los elementos de $E$, por ejemplo, como distintos errores, y las aplicaciones de nuestra categoría como aplicaciones implementadas en algún lenguaje de programación, entonces podemos intuir mejor qué exactamente cumple la multiplicación $\eta$. Consideramos dos morfismos $f:A\to TB$ y $g:B\to TC$ de la categoría Kliesli $\mathsf{C}_T$, o sea computaciones que tienen la opción de producir salida de $E$. Supongamos que su comportamiento se ve así:
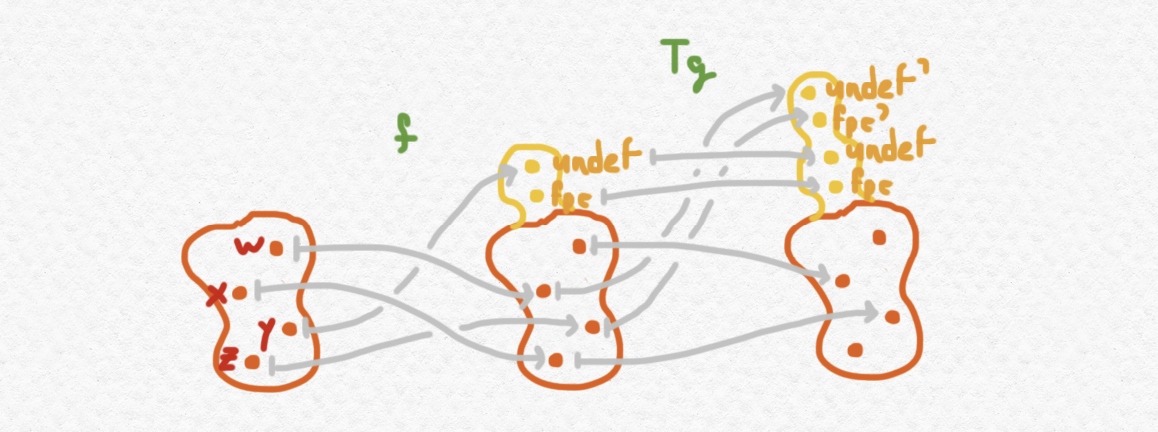
Fíjate que si componemos $Tg\circ f$ sin componer con la multiplicación $\mu_C$ al final, el codominio del morfismo resultante de $\mathsf{C}$ tiene cuatro valores excepcionales en vez de dos. En concreto estos cuatro valores distinguen entre valores excepcionales introducidos durante la evaluación de $f$, y los producidos durante la evaluación de $g$. Por ejemplo en el diagrama de arriba, $\mathtt{undef},\mathtt{fpe}$ representan valores excepcionales introducidos durante la evaluación de $f$ y $\mathtt{undef}',\mathtt{fpe}'$ representan valores excepcionales introducidos durante la evaluación de $g$. Como $f(y)$ es $\mathtt{undef}$ entonces $(Tg\circ f)(y)$ también tiene que ser $\mathtt{undef}$; por otro lado, se ve $f(w)$ no produce ningún valor excepcional pero $Tg(f(w))$ sí lo produce y en este caso la salida es $\mathtt{undef}'$ en vez de $\mathtt{undef}$ como el valor excepcional ha surgido de la evaluación de $g$. Ahora vamos al grano: la multiplicación $\mu_A$ colapsa las versiones distintas de los valores excepcionales de $E$ dejando de distinguir entre cuál aplicación lo ha producido. Mientras que el codominio de $Tg\circ f$ tiene cuatro valores excepcionales, $\mu_A\circ Tg\circ f$, o sea $g\circ_T f$, la composición de $f$ y $g$ en la categoría Kliesli, sólo tiene dos valores excepcionales.
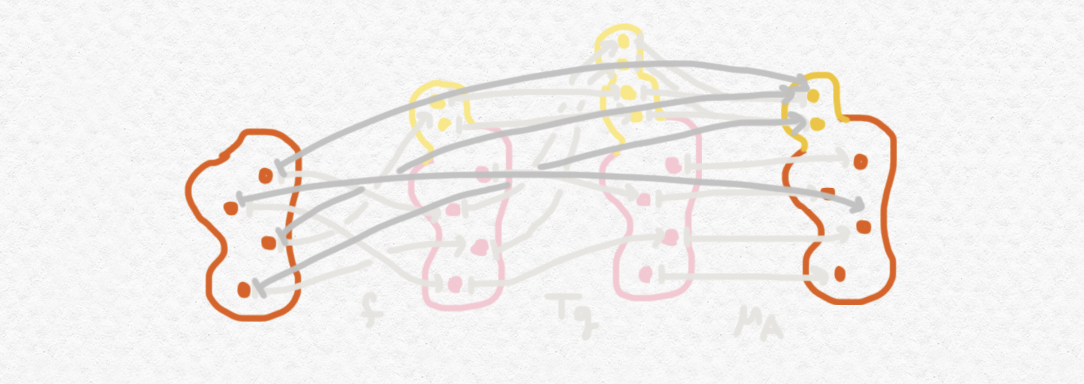
Ahora nos ponemos a describir una mónada que permite describir aplicaciones cuya salida posee cierto grado de incertidumbre. La mónada de distribución $D:\mathsf{Set}\to\mathsf{Set}$ es un funtor que lleva cada conjunto $A$ al conjunto de distribuciones probabilísticas en $A$ con soporte finito, es decir, un número finito de elementos de $A$ cada uno con una probabilidad asociada tal que todas las probabilidades se suman a $1$. Dado un conjunto $A$, se puede conceptualizar $DA$ como una generalización del conjunto $A$ que no sólo permite elementos de $A$ sino también "elementos borrosos" de $A$ que podrían ser o un valor u otro u otro aún con ciertas probabilidades. Por ejemplo, si $A={\mathtt{heads}, \mathtt{tails}}$ entonces los elementos de $DA$ representan todas las posibles monedas que se puede tirar para generar un resultado de o $\mathtt{heads}$ o $\mathtt{tails}$ al azar ya sean justas o parciales. Por ejemplo,
El funtor $D$ actúa sobre las aplicaciones así: mientras que $f:A\to B$ lleva elementos (deterministas) $a\in A$ a elementos (deterministas) $b\in B$, el morfismo $Df:DA\to DB$ lleva una distribución $\delta \in DA$ a la distribución del variable aleatorio que resulta de generar un valor aleatorio de $A$ según dictamina $\delta$ y entonces aplicar la función $f$, así generando un valor aleatorio de $B$. Por ejemplo, suponemos que $A={1,2,3,4,5,6}$ y así podemos interpretar los elementos de $DA$ como todos los posibles dados con $6$ caras (la mayoría de ellas parciales).
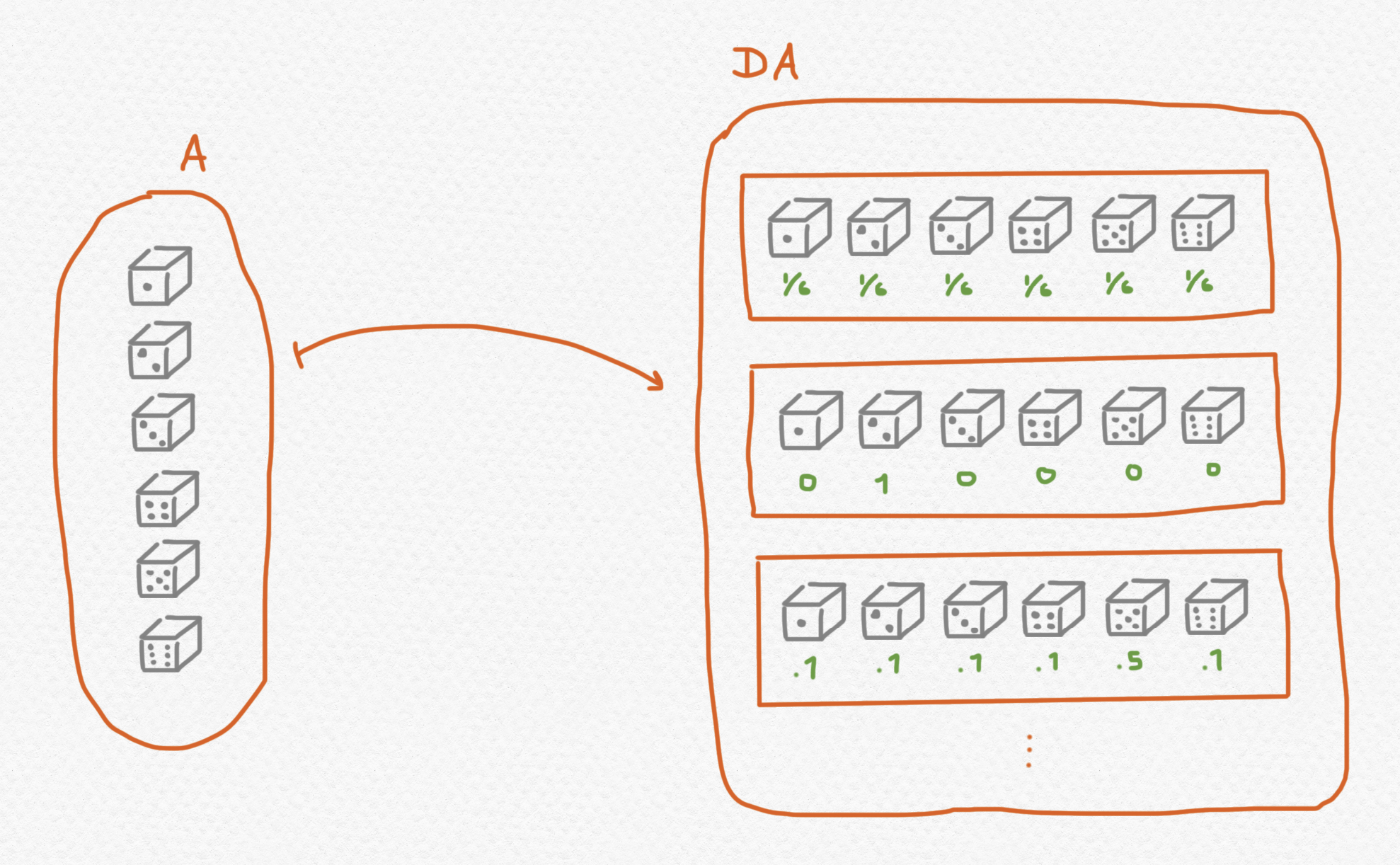
Hay una manera natural de incluir cada conjunto $A$ en el conjunto $DA$ de distribuciones probabilísticas en $A$: establecemos una correspondencia entre elementos $a\in A$ y "distribuciones triviales" que representan procesos aleatorios que siempre producen resultado de $a$ con certidumbre. Es decir que el elemento de $DA$ que le corresponde a $a\in A$ es la distribución que tiene probabilidad $1$ asociada a $a\in A$ y probabilidad $0$ asociada a cada otro elemento de $A$. Así definimos el componente $\eta_A$ de la unidad $\eta$ de nuestra mónada. Si representamos distribuciones como mapeos que se les asignan a elementos sus probabilidades respectivas (de tal manera que todas las probabilidades salvo un número finito son $0$) entonces podemos definir $\eta_A$ así: Y podríamos visualizar su acción en $A={1,2,3,4,5,6}$ así:
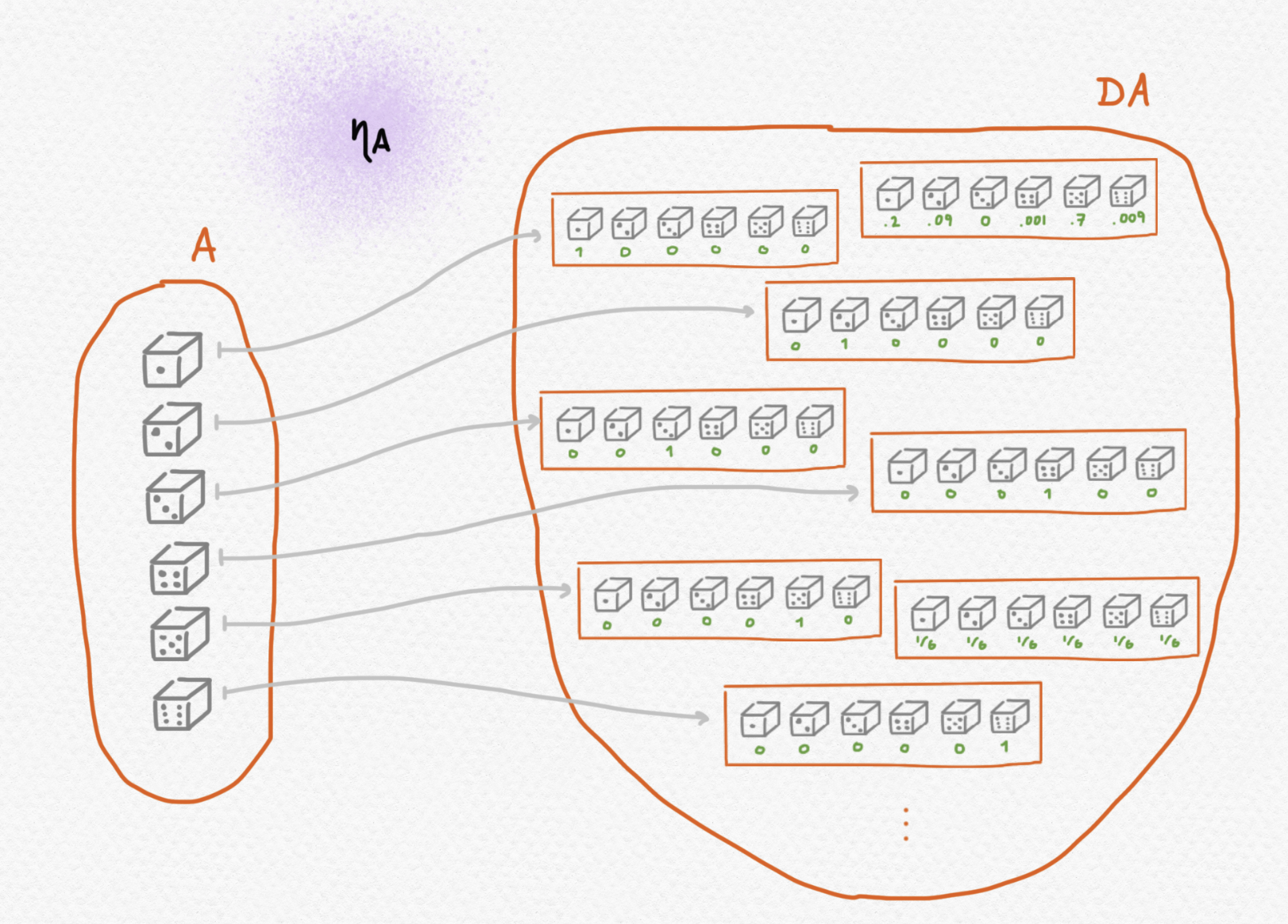
Y ¿qué tal la multiplicación de $D$? Pues para averiguar cómo definir $\mu$ hay que pensar en una manera natural de "reducir" un elemento de $DDA$ en un elemento de $DA$. Un elemento de $DDA$ sería una distribución de distribuciones, concepto que a primera vista parece muy rebuscado pero que se puede intuir así. Acudiendo otra vez al ejemplo del dado de $6$ caras, consideramos el elemento siguiente de $DDA$ con $A={1,2,3,4,5,6}$:
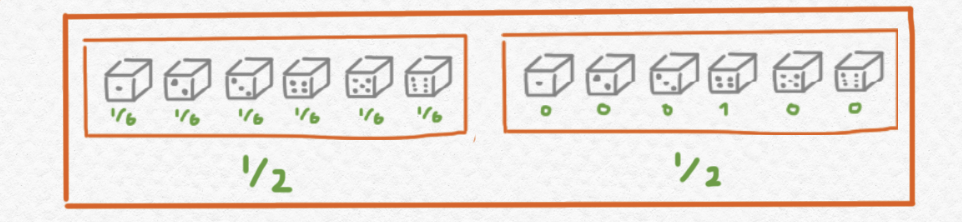
Yo describiría este elemento de $DDA$ intuitivamente como una distribución probabilística que encapsula el juego siguiente:
Tiras un dado de $6$ caras, pero no sabes si este dado es justo o no. Es posible - con probabilidad $1/2$ - que sea justo, pero también es posible - con igual probabilidad - que sea un dado que siempre cae con el lado $4$ arriba.
Fíjate que aunque el dibujo de arriba describe este jueguito, también se puede describir su resultado con una distribución sencilla de $DA$. En concreto, la probabilidad de tirar un $4$ al final del juego iguala mientras que la probabilidad de tirar cualquier uno de los otros números iguala Así que el resultado de este juego también está descrito por la distribución sencilla siguiente:
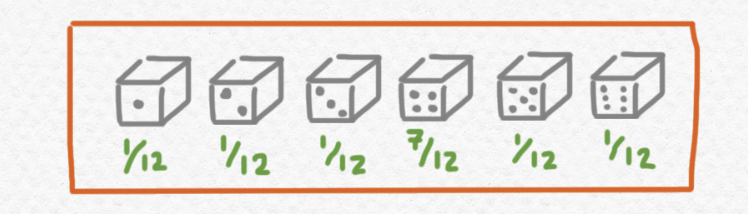
Para generalizar más, el hecho esencial sobre el índole de las distribuciones probabilísticas que estamos aprovechando aquí es el siguiente: elegir una distribución al azar (según una distribución de distribuciones) y entonces elegir un valor según esa distribución equivale a simplemente elegir un valor según alguna distribución, cuyas probabilidades se puede calcular a partir de los datos de la distribución de distribuciones y los datos de cada una de sus distribuciones con probabilidad no nula. Explícitamente, si $\delta\in DDA$ es una distribución de distribuciones, se puede calcular la distribución simple $\mu_A(\delta)$ que le equivale así:
Ahora nos ponemos a describir otro ejemplo un poco más complejo para demostrar como funciona la composición en la categoría Kliesli que surge de esta mónada. Mientras que una aplicación $f:A\to B$ entre conjuntos produce una salida determinista para cada entrada, un morfismo $f:A\to DB$ de $\mathsf{Set}_D$ se puede interpretar como una "aplicación no determinista" que podría producir distintos elementos de $B$ con probabilidades que varían dependiendo del argumento. Consideramos la situación siguiente:
Podemos conceptualizar $f:A\to DB$ como una función que se usa para seleccionar y tirar una moneda:
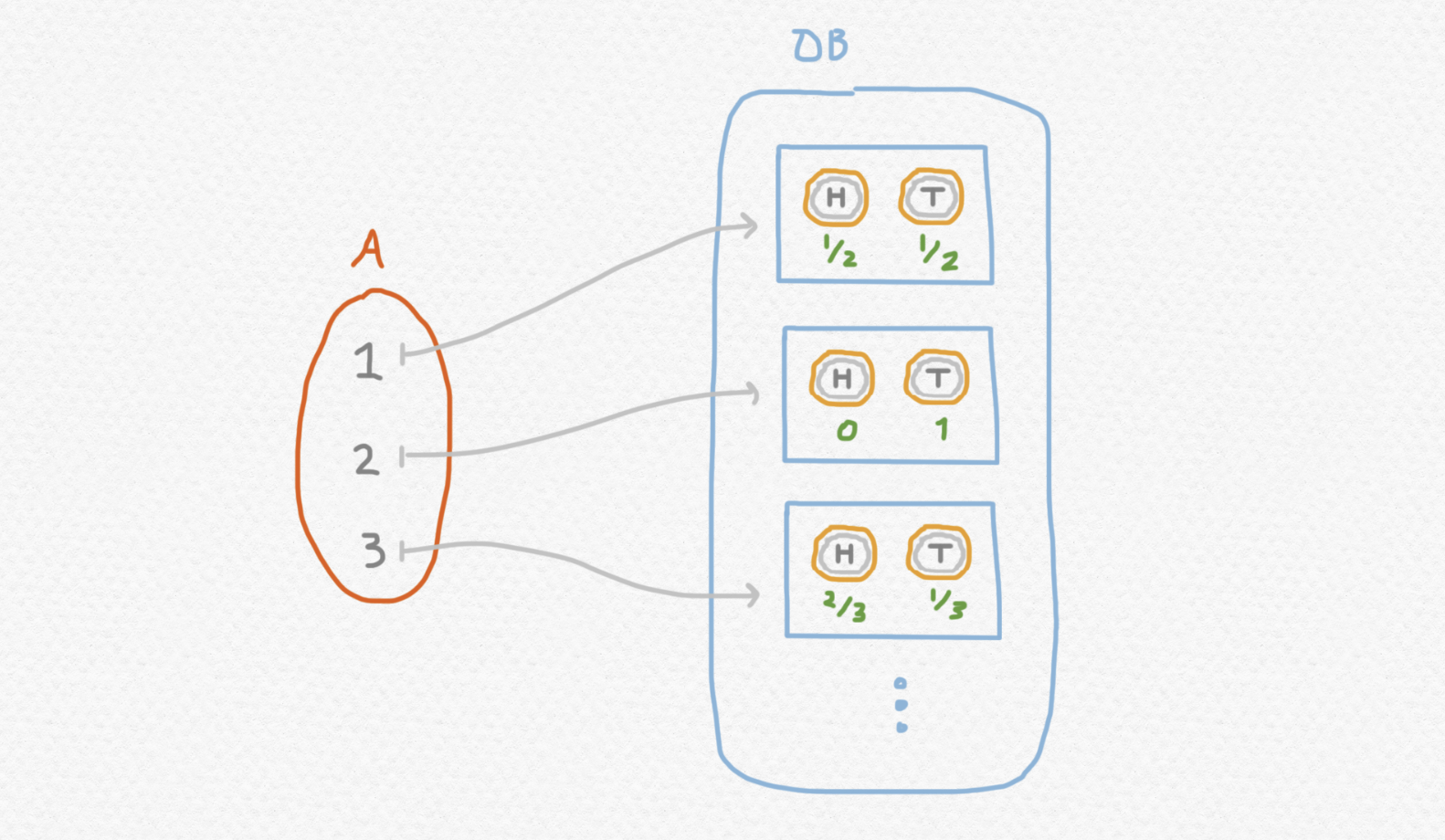
y $g:B\to DC$ como una función que elige y tira un dado a partir del resultado de tirar la moneda:
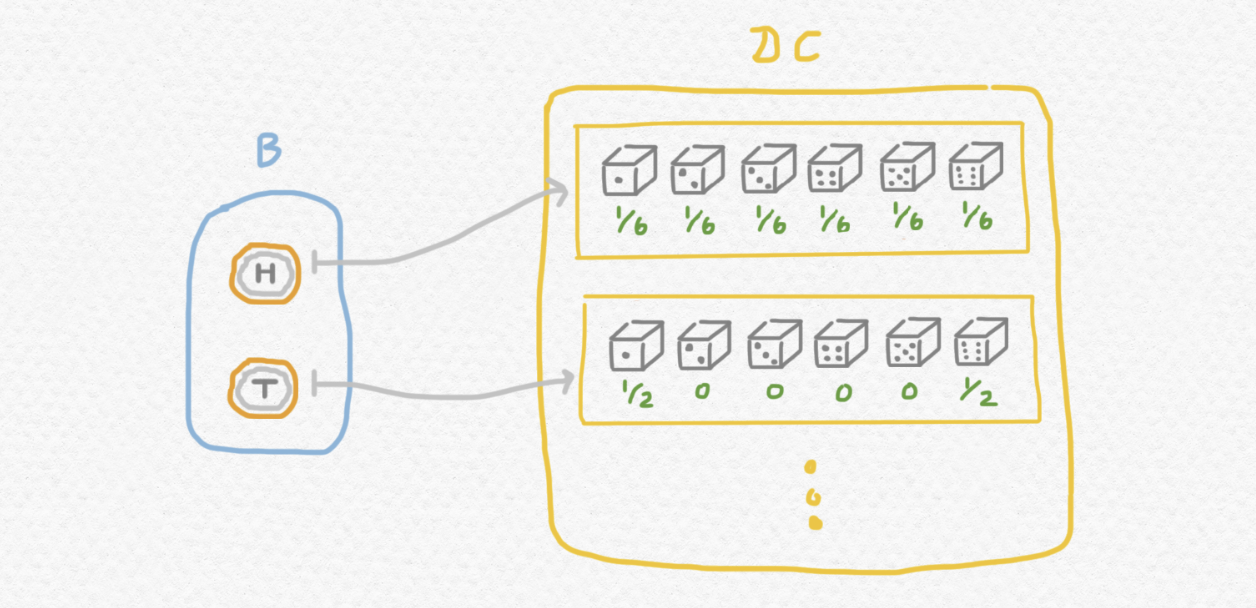
Si simplemente componemos $Dg\circ f$ entonces el codominio del morfismo que resulta constará de distribuciones de distribuciones:
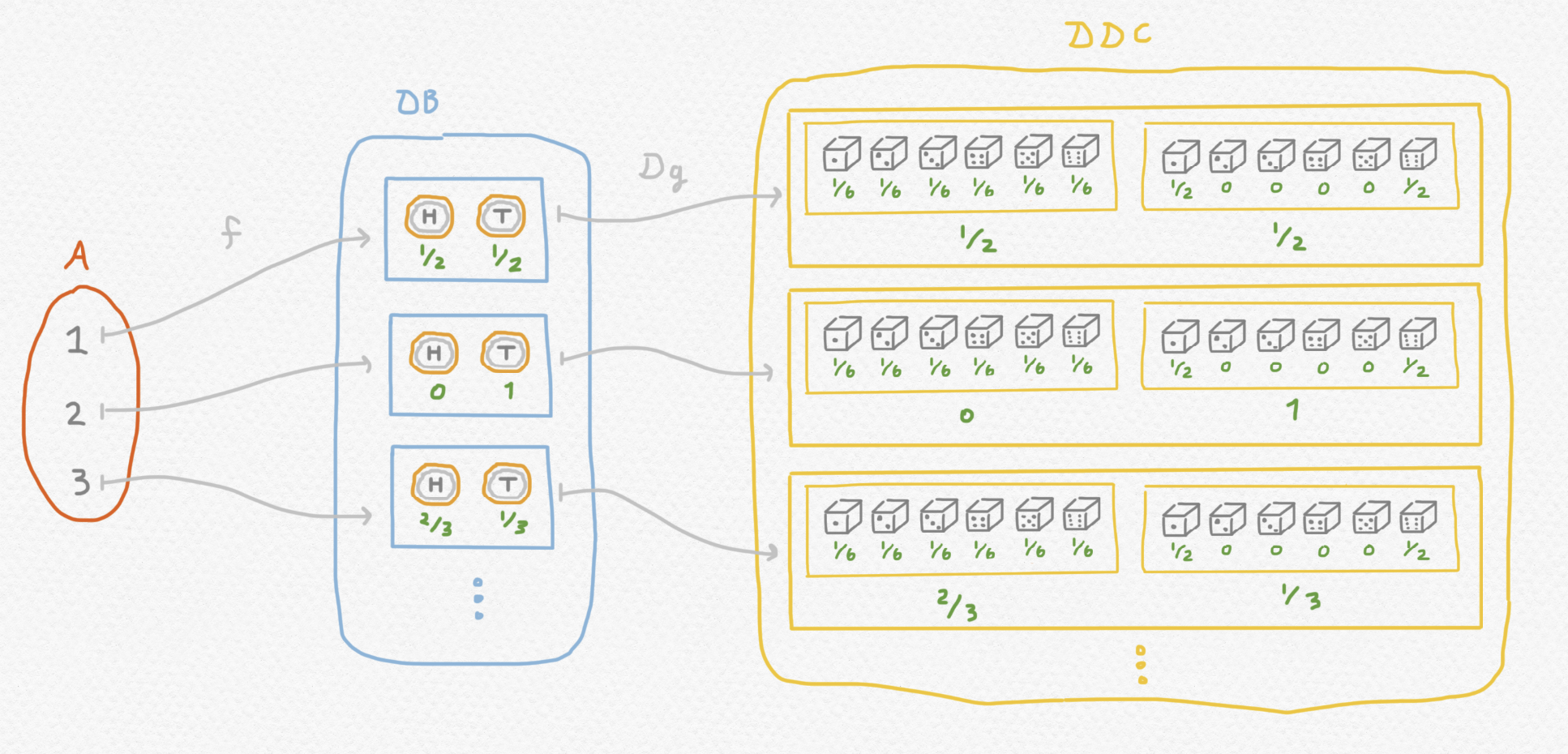
Pero como hemos comentado, no hace falta distribuciones anidadas para describir el resultado de un tal juego. Entonces aplicamos la multiplicación $\mu_C$ del mónada al final y obtenemos $\mu_C\circ Dg\circ f$, aplicación que se le asigna a cada una de las tres opciones ${1,2,3}$ la distribución del variable aleatorio que describe el resultado final de todo el juego a partir de la opción inicialmente elegida:
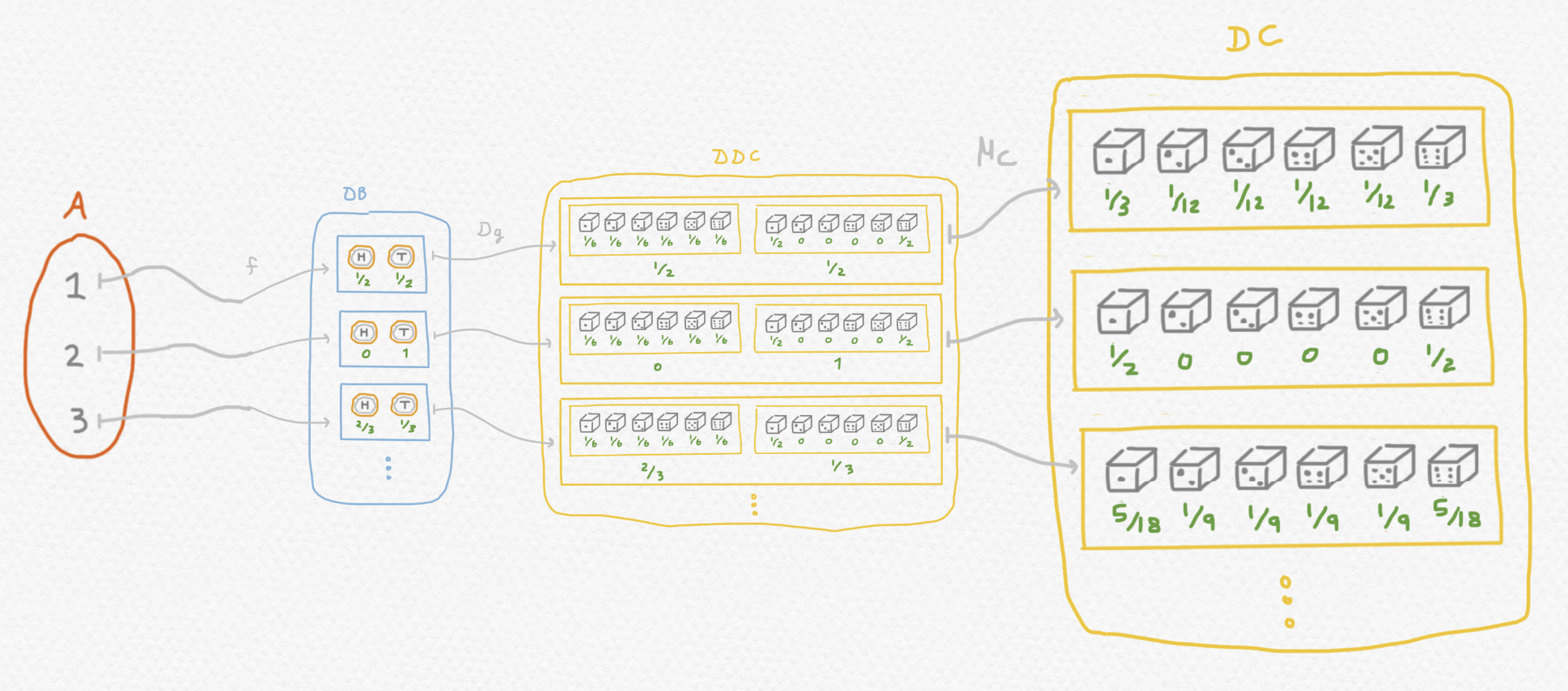
En las matemáticas hay una manera general de describir diversos tipos de estructuras algebraicas. Se puede definir un sistema algebraico como una tupla $\langle \Omega, E\rangle$ en la cual $\Omega$ es una lista de nombres de funciones con diversas aridades o sea diversos números de argumentos (incluso a veces funciones nularias o sea funciones que no aceptan ningunos argumentos y por eso en esencia son constantes) y $E$ es una lista de identidades universales o sea ecuaciones que involucran las funciones de $\Omega$ y varios variables libres. Entonces un $\langle \Omega,E\rangle$ álgebra es una estructura que consta de un conjunto de elementos $A$ y para cada aplicación abstracta de $\Omega$ con aridad $n$ una aplicación concreta $A^n\to A$ con la aridad especificada, tal que las aplicaciones concretas proporcionadas realmente satisfacen las identidades alistadas en $E$.
Por ejemplo, se puede definir un semigrupo como un $\langle \Omega,E\rangle$ álgebra donde $\Omega$ consta de un sólo símbolo $f$ de aridad $2$ que representa la operación binaria del semigrupo: y $E$ consta de la única identidad universal siguiente que asevera la asociatividad del semigrupo: que representa la ley asociativa del semigrupo. Un monoide es levemente más complicado: consiste en un semigrupo con un elemento identidad, que podríamos representar agregando un símbolo a $\Omega$ para una función nularia: y también hay que agregar una nueva identidad universal a $E$ para exigir que el nuevo símbolo $e$ se comporte como una identidad con respecto a la operación $f$: Podemos modificar $\Omega$ y $E$ otra vez para describir un grupo como un sistema algebraico. Como un grupo consta de un monoide que posee inversos para cada elemento, agregamos una tercera función para invertir los elementos de la álgebra: y un par más de leyes universales para especificar que $i(a)$ se comporta como inverso de $a$ con respecto a la operación $f$:
De todos modos, nos enfocamos en álgebras mucho más sencillos porque nuestro propósito principal no es profundizar en los entresijos de la álgebra universal sino conocer algunos ejemplos interesantes de mónadas. Nosotros consideraremos la el sistema algebraico con una función unaria y una binaria y ningunas identidades universales: Dado un sistema algebraico $\langle \Omega,E\rangle$ y un conjunto $A$, existe un álgebra $FA$ que se llama la "álgebra libre" en $A$. No voy a incluir una descripción precisa de esta álgebra pero se la puede conceptualizar como una álgebra que consta de los elementos de $A$ y del "máximo número de elementos distintos" que se puede alcanzar aplicando las funciones proporcionadas a los elementos de $A$. En nuestro caso concreto se puede imaginar los elementos de la álgebra libre $FA$ como expresiones no evaluadas que involucran los elementos de $A$ como "variables" y las funciones proporcionadas por $\Omega$. (Exploré algo semejante en una entrada anterior.)
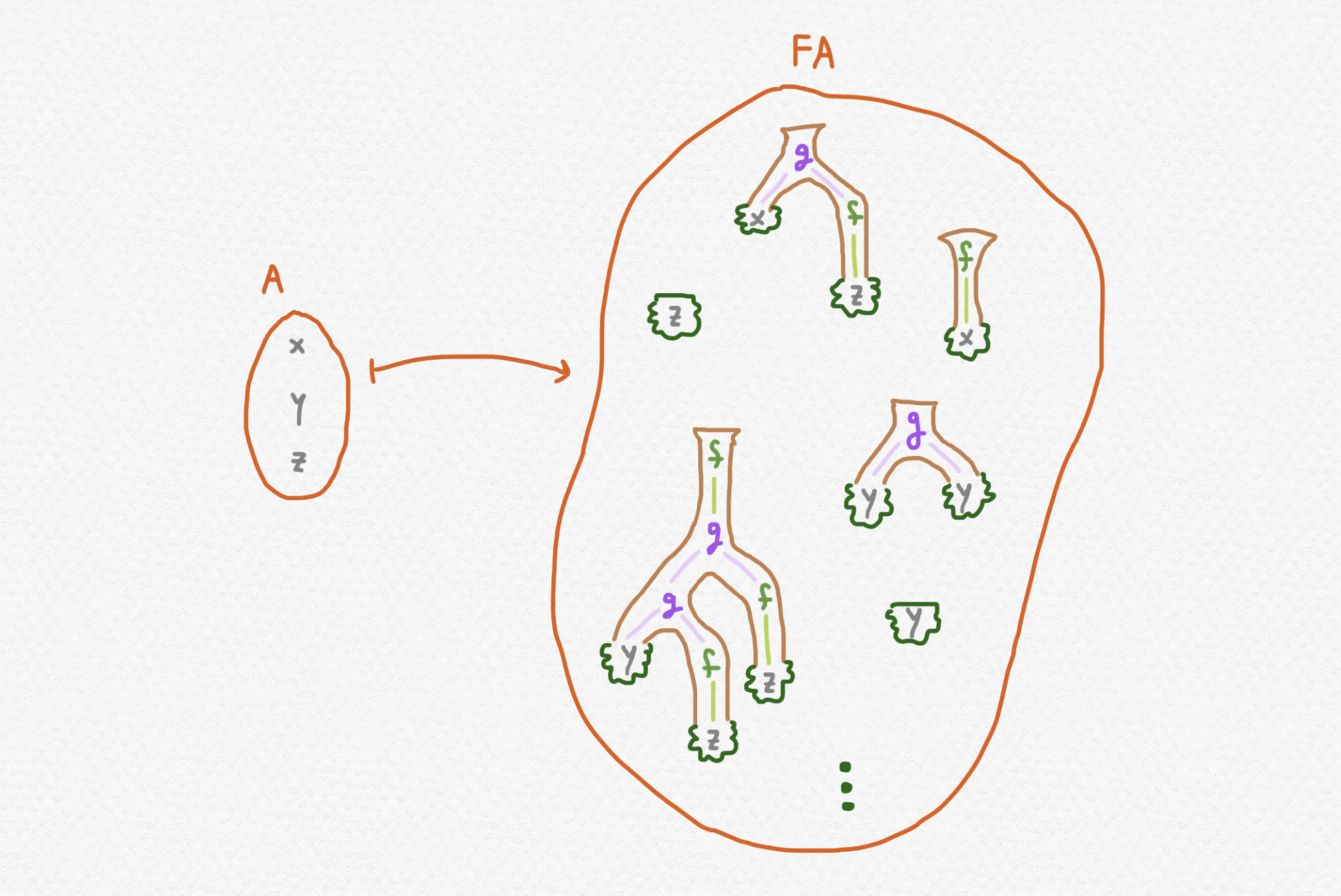
En el dibujo arriba, por ejemplo, los árboles mostrados dentro de $FA$ representan las expresiones respectivamente. Se ve del dibujo que estos arboles de $FA$ tienen elementos del conjunto $A$ en sus hojas y funciones de $\Omega$ en los demás nodos.
El funtor $F$ actúa sobre funciones $\varphi:A\to B$ entre conjuntos realizando sustituciones en las hojas de los arboles. En concreto si uno de los arboles $t\in FA$ tiene el elemento $a$ en una de sus hojas entonces el árbol transformado $F\varphi(t)\in FB$ tendrá el elemento $\varphi(a)$ de $B$ en su hoja correspondiente. Por ejemplo:
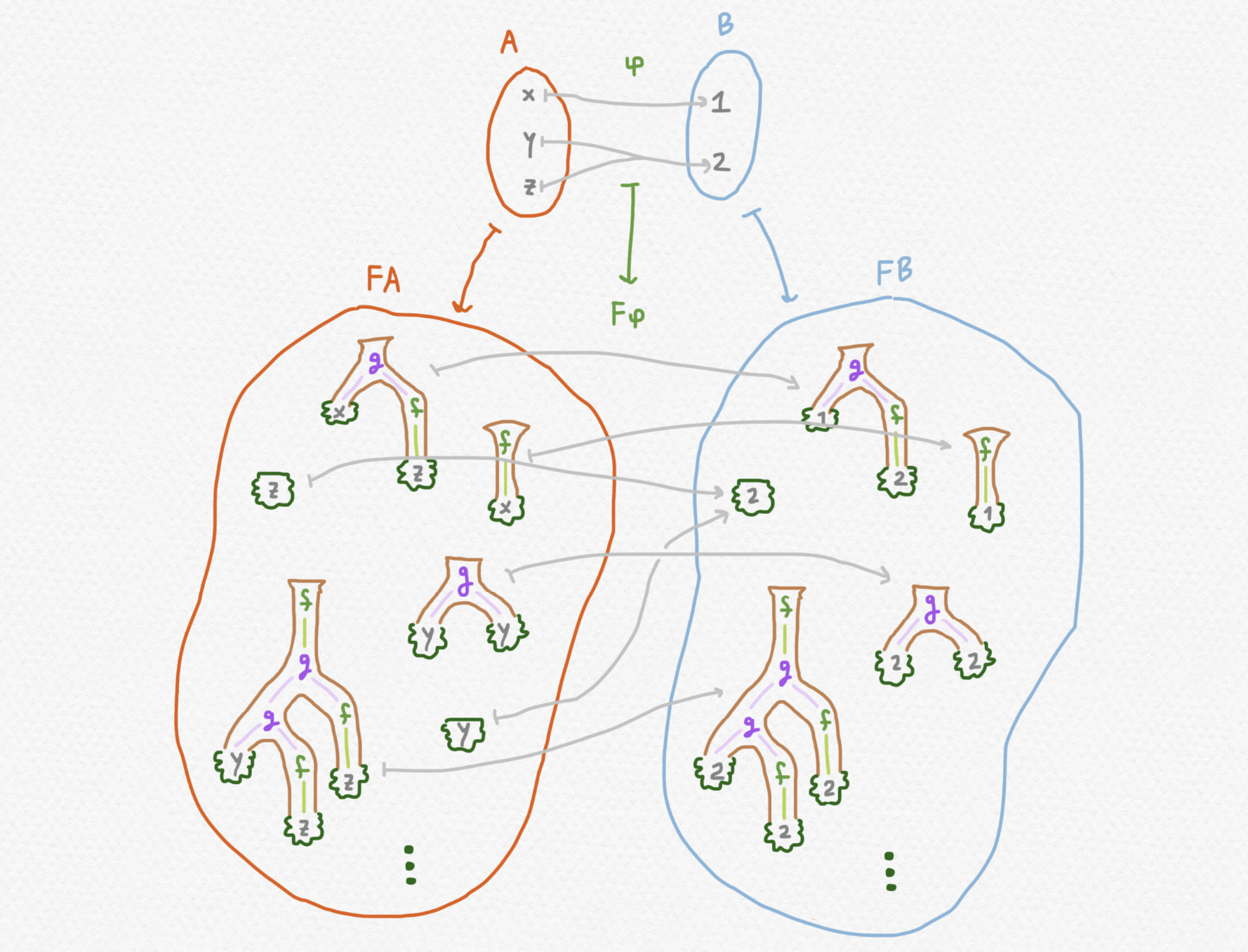
Este dibujo nos enseña como si $\varphi$ es una aplicación que tiene $\varphi(x)=\varphi(y)=1$ y $\varphi(z)=2$ entonces las expresiones anteriores se transformarán en las siguientes:
De inmediato vemos una manera muy natural de embeber cada conjunto $A$ en el conjunto $FA$ - podemos llevar cada elemento $a\in A$ al árbol de $FA$ con una única hoja que lleva el dato $a$. Así definimos el componente $\eta_A:A\to FA$ de la unidad $\eta:1_{\mathsf{Set}}\Rightarrow F$ de la mónada - pero ¿qué tal la multiplicación? Pues, a considerar cómo se ven los elementos del conjunto $FFA$. Estos serán árboles construidos utilizando las mismas funciones $f$ y $g$ pero con distintos datos en sus hojas. En los arboles de $FFA$, cada hoja de un árbol lleva dentro otro árbol perteneciente a $FA$. Aquí está un ejemplo de un tal elemento de $FFA$:
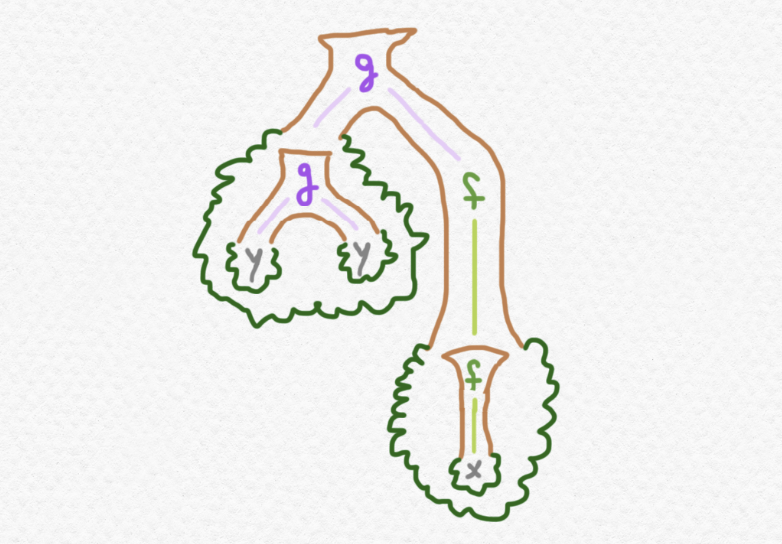
que representa la expresión siguiente:
El uso de colores en esta expresión sirve para desambiguar, pues si escribiera solamente
sin color ninguno, entonces no distinguiría la notación entre el árbol anteriormente dibujado y el siguiente, por ejemplo:
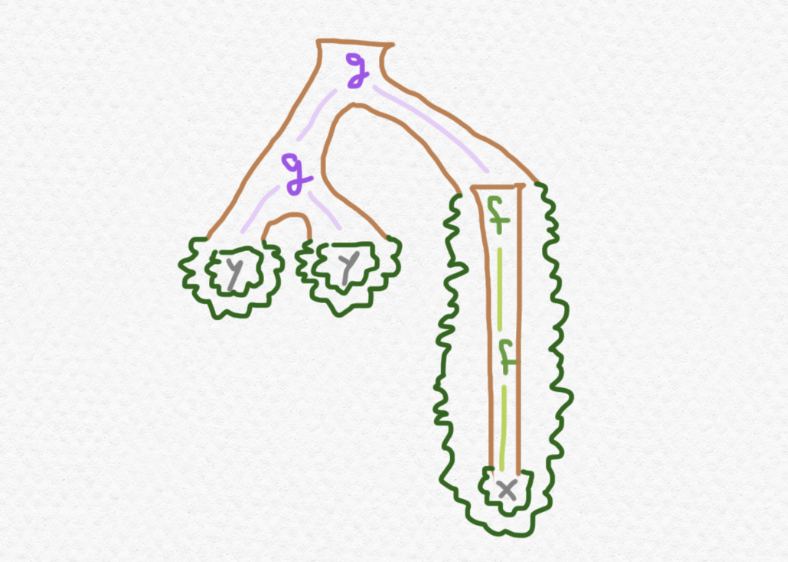
un árbol que, en nuestra notación colorada, se puede expresar sin ambigüedad así:
Al mirar estos dibujos, tal vez se te ocurre que estos dos "arboles de arboles" de $FFA$ son sospechosamente parecidos al siguiente árbol ordinario de $FA$:
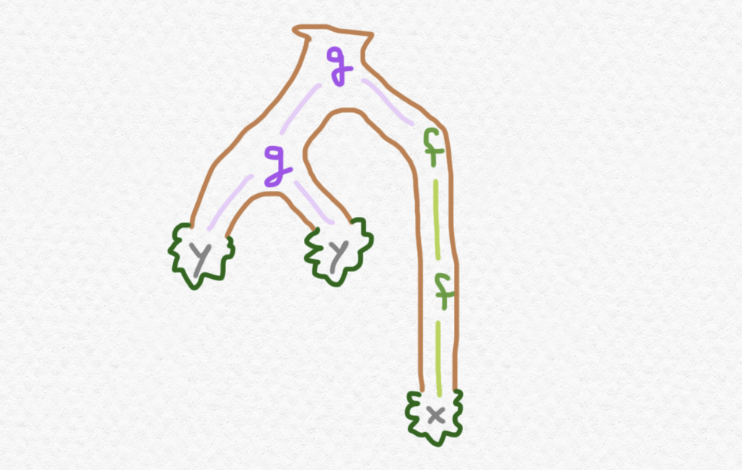
De esa observación surge la definición de la multiplicación de esta mónada. Es decir, el componente $\mu_A:FFA\to FA$ convierte cada árbol de arboles en un árbol ordinario extrayendo el árbol almacenado en cada hoja y empalmándolo con el árbol más grande en esa ubicación, de tal manera que las hojas del árbol resultante constan de las hojas agregadas de todos los arboles presentes en las hojas del "meta-árbol".
Entonces, mientras que una función $\varphi:A\to B$ de $\mathsf{Set}$ está transformado en una función $F\varphi:FA\to FB$ que realiza sustituciones de un variable por otro en las hojas de los arboles de $FA$, los morfismos de la categoría Kliesli $\mathsf{Set}_F$ realizan sustituciones de las hojas por otros arboles enteros. En concreto, si $\varphi:A\to FB$ es morfismo de $\mathsf{Set}_F$ que se le asigna a cada elemento de $A$ un árbol de $FB$, y si $\lambda:B\to FC$ es otro morfismo de $\mathsf{Set}_F$ que se le asigna a cada elemento de $B$ un árbol de $FC$, entonces el morfismo $\lambda\circ_F\varphi$ o sea $\mu_C\circ F\lambda\circ\varphi$ es lo que resulta de reemplazar cada hoja de cada árbol que sale de $\varphi$ que lleva un elemento $b\in B$ con el árbol $\lambda(b)$, empalmando éste en lugar de la hoja que llevaba el $b$.
Para crear una mónada en Haskell, hay que realizar tres pasos:
Functor describiendo cómo transforma los morfismos Monad proporcionando funcionalidad que equivale a la definición de la unidad y multiplicaciónAl definir una mónada en Haskell no se define directamente la unidad $\eta$ y la multiplicación $\mu$ sino un operador llamado "unir" ("bind" en inglés) que se denota x >>= f. En términos de la maquinaria matemática de la cual dispone una mónada, se puede definir el unir así: si $T:\mathsf{C}\to\mathsf{C}$ es una mónada, $a$ es un elemento de $TA$ y $f:A\to TB$ es un morfismo en la categoría Kliesli, entonces se define x >>= f como $\mu_B\circ Tf(x)$. Se puede entender la operación de unir como el homólogo de evaluación en la categoría Kliesli: mientras que la composición ordinaria $g\circ f$ de dos funciones corresponde a la composición $\mu_C\circ Tg\circ f$ en la categoría Kliesli, una evaluación ordinaria $f(x)$ de una función en un valor corresponde al unir x >>= f.
Vamos a intentar reproducir la mónada de valores excepcionales que hemos descrito en Haskell. Si para $E$ elegimos una colección de dos valores excepcionales, los cuales llamaremos Exn1 y Exn2 en Haskell, podemos definir un tipo parametrizable para nuestro funtor $T$ así:
data TwoExns a = Okay a | Exn1 | Exn2
deriving Show
Esta declaración dictamina que para algún tipo concreto a, para construir un elemento de TwoExns a, se puede proporcionar un elemento de a, o bien usar cualquier uno de los elementos fijos Exn1 y Exn2. Para instanciar este tipo parametrizable en la clase Functor hace falta proporcionar una definición de fmap :: (a -> b) -> TwoExns a -> TwoExns b, aplicación que describe cómo nuestro funtor transformará los morfismos. Aquí está nuestra definición:
instance Functor TwoExns where
fmap f (Okay x) = Okay (f x)
fmap f Exn1 = Exn1
fmap f Exn2 = Exn2
Ahora, a instanciar TwoExns en Monad. A propósito, salté un paso necesario, que es que Haskell precisa que instancie un funtor en otra clase que se llama Applicative antes de Monad. Como no quiero profundizar en los funtores aplicativos en esta entrada voy a simplemente pegar mi código aquí:
instance Applicative TwoExns where
pure x = Okay x
(Okay f) <*> (Okay x) = Okay (f x)
Exn1 <*> (Okay x) = Exn1
Exn2 <*> (Okay x) = Exn2
tf <*> Exn1 = Exn1
tf <*> Exn2 = Exn2
Lo único aquí que hay que comentar es la función pure :: a -> TwoExns a, que servirá como nuestra implementación de la unidad $\eta$ especificando cómo se incluye un tipo a en TwoExns a. Tal y como describimos anteriormente, embebemos a en TwoExns a estableciendo una correspondencia entre los elementos de a y los elementos de TwoExns a que no sean valores excepcionales, es decir los valores producidos con el constructor Okay. Al final instanciamos nuestro funtor como una mónada:
instance Monad TwoExns where
Exn1 >>= f = Exn1
Exn2 >>= f = Exn2
(Okay x) >>= f = f x
Como describimos antes, si pasamos un valor excepcional como entrada en un morfismo de la categoría Kliesli, entonces devuelve ese valor excepcional mismo, mientras que si pasamos un valor "ordinario" entonces evaluamos la función en este valor.
Ahora pasamos a implementar la mónada de álgebra libre que hemos visto anteriormente, en concreto la que corresponde al sistema algebraico en el que $\Omega$ posee una función unaria $f$ y una binaria $g$ y $E={}$. Por ahora voy a saltar la mónada de distribución para tratarla al final, como es la mónada más difícil de implementar en Haskell de los tres.
Representamos el tipo de dato de los arboles así:
data AlgTree a = Leaf a
| ApplyF (AlgTree a)
| ApplyG (AlgTree a) (AlgTree a)
Así, una expresión como $\mathtt{g(f(1),2)}$ en nuestra notación anterior se representaría como ApplyG (ApplyF (Leaf 1)) (Leaf 2) en Haskell. Nuestra implementación de fmap será así:
instance Functor AlgTree where
fmap f (Leaf x) = Leaf (f x)
fmap f (ApplyF t) = ApplyF (fmap f t)
fmap f (ApplyG t1 t2) = ApplyG (fmap f t1) (fmap f t2)
Fíjate que cuando se aplica fmap f a un árbol cuyo primer nodo no es una hoja sino ApplyF o ApplyG, entonces fmap f se propaga por los subarboles hacia abajo hasta llegar a las hojas, donde al final aplica f directamente a los datos presentes en las hojas. O sea, se sustituyen los valores en las hojas por sus valores correspondientes de f, tal y como hemos descrito la acción de este funtor anteriormente.
Aquí instanciamos el funtor como un funtor aplicativo, que no comento más excepto para indicar que pure actúa sobre los datos exactamente como hemos descrito la unidad $\eta$ antes, es decir simplemente envolviendo cada dato en una hoja del árbol:
instance Applicative AlgTree where
pure x = Leaf x
tf <*> (Leaf x) = fmap ($ x) tf
tf <*> (ApplyF t) = ApplyF (tf <*> t)
tf <*> (ApplyG t1 t2) = ApplyG (tf <*> t1) (tf <*> t2)
y por fin estamos listo para definir AlgTree como una mónada. Aquí definimos la operación de unir:
instance Monad AlgTree where
(Leaf x) >>= f = f x
(ApplyF t) >>= f = ApplyF (t >>= f)
(ApplyG t1 t2) >>= f = ApplyG (t1 >>= f) (t2 >>= f)
Es que para aplicar un morfismo de la categoría Kliesli a un árbol, tiene que propagarse hasta las hojas del árbol para allí sustituir otro árbol (el que corresponde con el dato de esa hoja) en esa ubicación. Fíjate que aunque la definición recursive de t >>= f es muy parecido a la definición de fmap f t, si f es del tipo f :: a -> AlgTree b, entonces la expresión t >>= f será del tipo AlgTree b pero la expresión fmap f t será del tipo AlgTree (AlgTree b). Es por eso que en la definición del unir para el caso de ser t una hoja, escribimos (Leaf x) >>= f = f x en vez de (Leaf x) >>= f = Leaf (f x) (lo cual produciría un error de tipos).
Ahora veremos la implementación del ejemplo más difícil de implementar en Haskell de los tres. Representaremos una distribución sobre el tipo a como una lista de pares de elementos de a con números de punto flotante, tal que el tipo de distribuciones (con soporte finito) sobre a será [(a, Float)]. Así que ponemos la definición siguiente:
data Distr a = Distr { getData :: [(a, Float)] }
deriving Show
Pues, como Haskell es un lenguaje perezoso, esto realmente permitiría la construcción de distribuciones con soporte infinito. Además, permite la construcción de distribuciones que ni son válidas, por ejemplo listas de pares en las cuales las probabilidades (i.e. los segundos elementos de los pares) no se suman a $1$. No hay manera de asegurar una tal cosa en Haskell (que sepa yo... en un lenguaje como Agda, sí) así que simplemente asumiremos que todas las instancias construidas serán distribuciones bien definidas.
El lío viene cuando intentamos instanciar este tipo parametrizado en la clase Functor. Tal y como hemos descrito la acción de este funtor en el apartado anterior, fmap f debe actuar sobre una distribución aplicando la función f a los primeros componentes de los pares de la lista y entonces combinando los pares con el mismo primer elemento. Por ejemplo, si tenemos una distribución y queremos aplicar, digamos, la función $\mathtt{mod2}$ que calcula el resto módulo $2$ de un número entero, entonces el resultado no debe de ser sino Así que, nuestra implementación de fmap no solo debe aplicar una función a los primeros elementos de todos los pares sino también "compactar" los pares combinando pares que representan el mismo resultado. Pero de eso consta el problema: en Haskell no es cierto que todos los tipos vienen equipados con una función (==) :: a -> a -> Bool para comprobar la igualdad de elementos. Hay una clase que se llama Eq cuyas instancias son los tipos que llevan un comprobador de igualdad. Pero para instanciar Distr en Functor sería preciso poder comprobar la igualdad de los elementos de cualquier tipo lo cual no es posible.
Por eso, realmente no podemos instanciar Distr en Functor ni en Monad. En vez de hacer eso, definiremos clases propias que se parecen a Functor y Monad pero que operan sobre todos los tipos sino sólo los tipos en los cuales se puede realizar comprobaciones de igualdad. De hecho, para simplificar las cosas no exigiremos que los tipos sean instancias de Eq sino de Ord, otra clase que representan tipos cuyos elementos pueden ser ordenados y comparados. Cualquiera instancia de Ord también es instancia de Eq, pues se puede determinar si x iguala y comprobando si x <= y y entonces si x >= y. Las definiciones de Functor y Monad usadas en Haskell son las siguientes:
class Functor f where
fmap :: (a -> b) -> f a -> f b
class Monad m where
(>>=) :: m a -> ( a -> m b) -> m b
(>>) :: m a -> m b -> m b
return :: a -> m a
pero nosotros definiremos clases propias semejantes que se llaman OrdFunctor y OrdMonad:
class OrdFunctor f where
ordFmap :: (Ord b) => (a -> b) -> f a -> f b
class OrdMonad t where
oBind :: (Ord b) => t a -> (a -> t b) -> t b
oReturn :: a -> t a
Fíjate que ordFmap sólo exige la posibilidad de comprobaciones de igualdad en el codominio de una función porque el cálculo involucrado no precise comparaciones de las entradas a la función sino sólo los valores devueltos.
Antes de instanciar Distr en OrdFunctor y OrdMonad vamos a definir un par de funciones útiles para la manipulación de distribuciones:
reduceDistr :: (Ord a) => Distr a -> Distr a
reduceDistr (Distr d) =
Distr (sortBy (\x -> \y -> compare (fst x) (fst y))
(filter (\p -> (snd p) > 0)
(map (second (sum . (map snd)))
(filterOnKey fst d))))
distrEq :: (Ord a) => Distr a -> Distr a -> Bool
distrEq dd1 dd2 = (getData $ reduceDistr dd1) == (getData $ reduceDistr dd2)
La función reduceDistr sirve para reescribir una distribución en una forma "canónica" para poder compararlas. Por ejemplo, las dos distribuciones
realmente nos parecen maneras rebuscadas de representar la misma distribución, que se escribe de la forma "más natural" así: Lo que hace reduceDistr es combinar pares que corresponden al mismo resultado agregando sus probabilidades, eliminando por completo los resultados con probabilidad igual a $0$ y al final ordenando los pares de la lista según el orden de los elementos de a en sus primeras entradas. Por ejemplo, para las distribuciones d1 y d2 definidas anteriormente, la salida de reduceDistr d1 tanto como de reduceDistr d2 será exactamente la tercera lista más "limpia" mostrada arriba. La segunda función distrEq utiliza reduceDistr para determinar si dos distribuciones son iguales reduciéndolas a sus formas canónicas respectivas y comparando esas como listas.
Otra maquinaria que tenemos que proporcionar es una manera de ordenar los elementos de Distr a dado una manera de ordenar los de a. Pues si queremos poder manipular morfismos de la categoría Kliesli, necesitaremos poder formar composiciones de la forma $\mu_C\circ Dg\circ f$, la cual involucraría computar fmap g donde g es una función con signatura g :: a -> Distr b para algunos tipos a y b, pero como fmap g exige que el codominio de g lleve una estructura ordenada, que en este caso es el tipo Distr b. Imponemos un orden lexicográfico en los tipos de distribuciones:
instance (Ord a) => Ord (Distr a) where
(Distr d1) <= (Distr d2)
= if d1 == [] then True else
if fst (head d1) <= fst (head d2) then True else
if snd (head d1) <= snd (head d2) then True else
(Distr (tail d1)) <= (Distr (tail d2))
Ahora por fin estamos listo para instanciar Distr en OrdFunctor y OrdMonad:
instance OrdFunctor Distr where
ordFmap f (Distr d) = reduceDistr (Distr (map (first f) d))
instance OrdMonad Distr where
oBind (Distr d) f
= reduceDistr
(Distr
(concatMap
(\(x, p) -> map (second (p *)) ((getData . f) x))
d))
oReturn x = Distr [(x, 1)]
Aquí sólo estamos implementando las leyes de la probabilidad y aprovechando de nuestra implementación anterior de recudeDistr para limpiar los resultados de las computaciones. Ahora que tenemos las implementaciones podemos intentar replicar el ejemplo rebuscado con monedas y dados que construimos anteriormente. Aquí definimos las dos funciones $f,g$ usadas en el ejemplo, donde representamos los dos lados de la moneda con True y False de tipo Bool:
f :: Integer -> Distr Bool
f x = if x == 1 then Distr [(True, 0.5), (False, 0.5)] else
if x == 2 then Distr [(False, 1.0)] else
if x == 3 then Distr [(True, 0.67), (False, 0.33)] else
Distr [(True, 1.0)]
g :: Bool -> Distr Integer
g True = Distr (map (\x -> (x, 1.0/6)) (take 6 [1..]))
g False = Distr [(1, 0.5), (6, 0.5)]
y ahora podemos calcular $(g\circ_D f)(1), (g\circ_D f)(2)$ y $(g\circ_D f)(3)$ para comprobar si tienen las mismas probabilidades como las alistadas en nuestro dibujo anterior. En el REPL realizamos estas tres computaciones usando oBind y oReturn:
ghci> oBind (oBind (oReturn 1) f) g
Distr {getData = [(1,0.33333334),(2,8.3333336e-2),(3,8.3333336e-2),(4,8.333333336e-2),(5,8.3333336e-2),(6,0.33333334)]}
ghci> oBind (oBind (oReturn 2) f) g
Distr {getData = [(1,0.5),(6,0.5)]}
ghci> oBind (oBind (oReturn 3) f) g
Distr {getData = [(1,0.27666667),(2,0.11166667),(3,0.11166667),(4,0.11166667),(5,0.11166667),(6,0.27666667)]}
los cuales valores están de acuerdo con los valores fraccionales exactos de nuestro dibujo anterior.