Counting elements of lists in Agda

In this entry, I just want to describe a simple concept that I've personally had a lot of trouble grasping that involves case splits in the proof assistant Agda. I've written a couple of posts in the past involving Agda, such as this post introducing how type theory, and in particular the theory of dependent types, can help us represent mathematics programmatically with propositions and proofs corresponding to types and their elements. In this later post I dived a little deeper into the algebraic side of things, showing how a common tedious part of our proofs (involving repeated applications of associativity) can be automated. I'd recommend checking out these posts before reading this one, if you haven't already. I'll also use some of the more basic functions defined in Martín Escardó's notes, since this is where I've learned the most about proofwriting and foundations in Agda.

Originally, I was planning on writing this blog post about my attempt to implement the insertion sort algorithm in Agda and prove that it correctly sorts lists. This was a huge challenge, and I've spent several weeks puzzling over it between semesters, but I finally managed to make it work. But this would make for a monster of a blog post, and a lot of my more recent blog posts have ended up a lot longer than I meant for them to be. So, instead, I'll be zooming in on a small part of this much larger problem with a focus on the part that has given me the most trouble: case splits in proofs.

The statement we'll be trying to prove is the following:

Given two lists $\mathtt{ls1}$ and $\mathtt{ls2}$, the number of times that the element $a$ appears in $\mathtt{append}(\mathtt{ls1},\mathtt{ls2})$ equals the number of times that it appears in $\mathtt{ls1}$ plus the number of times that it appears in $\mathtt{ls2}$.

...to the surprise and amazement of nobody. The tricky part of this task is not really convincing ourselves that this is true, but convincing the type checker that this is true. (Although, to be honest, after explicitly and pedantically writing out all of the components of this proof in Agda, I do feel like I understand it on a deeper level, even if it seems like a "trivial" statement.)

We need to do a little bit of housekeeping first. We're going to use the following inductive definition of list types:

data List (A : 𝓤 ̇) : 𝓤 ̇ where
   [] : List A
   cons : A → List A → List A

The type $\mathtt{List} A$ is the type of lists of elements of $A$, where $A$ is any other type (in some type universe). There are only two ways of getting a list of elements of $A$ - we can either produce the empty list, or we can add an element of $A$ to the beginning of a preexisting list of elements of $A$. We aren't quite ready to formulate our statement, because we still need to tell Agda what we mean by "appending two lists" and "the number of times an element appears in a list". We can define an $\mathtt{append}$ function pretty easily as follows:

append : {A : 𝓤 ̇} → List A → List A → List A
append [] ls2 = ls2
append (cons x ls1) ls2 = cons x (append ls1 ls2)

Notice that we're pattern matching on the first argument. If the list we're prepending is empty, we don't need to make any changes to the second list. If the list we're prepending starts with some element $x$, then this will become the first element of the resulting list. Defining an "element counting" function involves a slight complication. To count the number of occurrences of some element $a:A$ in a list $\mathtt{ls}:\mathtt{List} A$, we have to iterate through the elements of the list, check whether each one of them is equal to $a$, and increment our result for each element that is equal to $a$. The problem is that it's not a given that every type is equipped with decidable equality. To write this function, we'll need a function that is capable of determining whether two given elements of $A$ are equal or not, i.e. a function with the type signature $$\prod_{a,a':A} \Big((a\equiv a')+ \neg(a\equiv a')\Big)$$ If we nonconstructively decide to assume the law of excluded middle, we can always procure a function of this type, since LEM allows us to construct elements of $P+\neg P$ for any type $P$. However, in order to keep things constructive and make the weakest assumptions necessary, we'll just assume that the type $A$ comes equipped with an "equality decider", and this assumption will take the form of an additional argument to our counting function. Hence, rather than writing a function with the type signature $$\mathtt{counts}: \prod_{A:\mathcal U} \Big(\mathtt{List} A \rightarrow A \rightarrow \mathbb N\Big)$$ we will write a function with the signature $$\mathtt{counts} ~ : ~ \prod_{A:\mathcal U} \bigg(\Big(\prod_{a, a':A}\mathtt{decidable}(a\equiv a')\Big)\rightarrow \mathtt{List} A \rightarrow A \rightarrow \mathbb N\bigg)$$ where $\mathtt{decidable}(P)$ represents $P+\neg P$. By the way, this problem is by no means unique to Agda. If you attempt to write a polymorphic function in Haskell with the type signature a -> [a] -> Int that counts the number of occurrences of some element in a list, you'll probably find yourself running into this issue as well. The solution is to add something called a constraint to the function signature, so that it looks like (Eq a) => a -> [a] -> Int. This has the effect of only allowing the type variable a to range over types that instance the Eq class, which requires its instances to possess an equality testing function == :: a -> a -> Bool, rather than allowing a to range over all types. This is pretty much analogous to the fix we've implemented above in Agda, where we accept an equality decider on $A$ as an additional argument to our counting function. Anyways, here's our counting function:

counts : {A : 𝓤 ̇} → has-decidable-equality A → List A → A → ℕ
counts deq [] a = 0
counts deq (cons x ls) a
  = +-recursion
      (λ _ → succ)
      (λ _ → id)
      (deq x a)
      (counts deq ls a)

What exactly is going on here? We're pattern-matching on the list argument, returning zero if the list is empty and recursing if the list has at least one element. Although the call to +-recursion is a little cryptic-looking, it's essentially a glorified if-else statement. The type signature of +-recursion, a function defined in Escardó's notes, is as follows: $$\prod_{A:\mathcal U}\prod_{B :\mathcal V}\prod_{C:\mathcal W}\Big((A\to C)\to (B\to C)\to (A+B)\to C\Big)$$ For any three types $A,B,C$, given a function $f:A\to C$ and another $g:B\to C$, it "smushes together" the domains of these two functions to form a function $h:A+B\to C$ originating from the coproduct $A+B$, so that the behavior of $h$ is determined by the behavior of $f$ on the "left side" of the coproduct and by $g$ on the "right side" of the coproduct. In particular, if this coproduct looks like $P+\neg P$ - i.e. a decision of whether the proposition $P$ is true or false - and if the functions $f$ and $g$ are constant and $\mathtt{dec}$ is something of type $P+\neg P$, then (+-recursion f g dec) produces the first constant if $P$ is true and the second constant if $P$ is false. In the above definition, the result of our evaluation of +-recursion is either the successor function succ (if x equals a) or the identity function id (otherwise). Hence, the effect is to increment the occurrence count of $a$ in the tail of the list if the first element is equal to $a$, or simply return the occurrence count of $a$ in the tail if the first element is not equal to $a$.

Now we're ready to at least state the proposition that we want to prove. Here is its type signature:

append-sum-counts :
  {A : 𝓤 ̇}
  → (deq : has-decidable-equality A)
  → (ls1 ls2 : List A)
  → (a : A)
  → counts deq (append ls1 ls2) a ≡ (counts deq ls1 a) +̇ (counts deq ls2 a)

To paraphrase this in English, given a type $A$, a function that decides equality of elements of $A$, two lists of type $\mathtt{List} A$, and an element $a:A$, the count of $a$ in the concatenation of the two lists (tallied using the provided equality deciding function) equals the sum of the counts of $a$ in the two lists separately (also tallied using the equality deciding function). We'll want to pattern match on the first input list for this proof, since the definition of append is defined in this way. The case when ls1 is empty is pretty easy to write:

append-sum-counts deq [] ls2 a = refl (counts deq ls2 a)

Why does this work? Agda knows from our definition of append that (append [] ls2) is defined to be equal to ls2, and it also knows that (counts deq [] a) is defined to be zero. Also, not only is $0+n$ equal to $n$ for any natural number $n:\mathbb N$, but this fact is part of the very definition of the addition function as it's defined in my arithmetic.agda module:

_+̇_ : ℕ → ℕ → ℕ
0 +̇ y = y
(succ x) +̇ y = succ (x +̇ y)

so Agda is able to determine without any help from us that counts deq (append [] ls2) a and (counts deq ls1 a) +̇ (counts deq ls2 a) are equal. It is capable of simplifying both of these expressions to (counts deq ls2 a) using only the definitions of the functions involved, allowing us to supply nothing more than refl (counts deq ls2 a).

The second case won't be quite as simple, and we'll see why in a second, but we can already start to sketch out in our heads what it should look like. Since we've already covered the case in which the first list is empty, the second case should define the proof append-sum-counts deq (cons x ls1) ls2 a in terms of previous proofs of simpler cases, most likely the case append-sum-counts deq ls1 ls2 a. We know that if x and a are equal, then appending x shouldn't change the occurrence count of a, so we can probably return the previous proof unchanged - but if they are equal, then both sides of the equality will be incremented, so we'll probably need to use an ap succ somewhere to transform the previous case into the current one. Since the way in which we transform the previous equality to obtain the desired equality depends on whether or not $x=a$, our proof will have to involve some kind of case split. Even though the proof may not seem terribly complicated, we're going to write a pair of helper functions first, one for each of these two cases, with the following type signatures:

cons-eq-succ-count :
  {A : 𝓤 ̇}
  → (deq : has-decidable-equality A)
  → (ls : List A)
  → (a x : A)
  → (x ≡ a)
  → (counts deq (cons x ls) a) ≡ succ (counts deq ls a)

cons-neq-same-count :
  {A : 𝓤 ̇}
  → (deq : has-decidable-equality A)
  → (ls : List A)
  → (a x : A)
  → ¬ (x ≡ a)
  → (counts deq (cons x ls) a) ≡ counts deq ls a

The first helper function will essentially be a proof that appending some element of $A$ that is equal to $a:A$ to a list will increment its count for that element, and the second will be a proof that appending an element distinct from $a$ will not affect the list's count for that element. Since this is essentially how we defined the counts function, it feels like these equalities should be completely definitional. For the first function, we might be tempted to write something like

cons-eq-succ-count deq ls a x eq = refl (succ (counts deq ls a))

but Agda's type checker does not like this: it's not capable of verifying that the two quantities are definitionally equal. It can simplify the expression (counts deq (cons x ls) a) to the following:

+-recursion
  (λ _ → succ)
  (λ _ → id)
  (deq x a)
  (counts deq ls a)

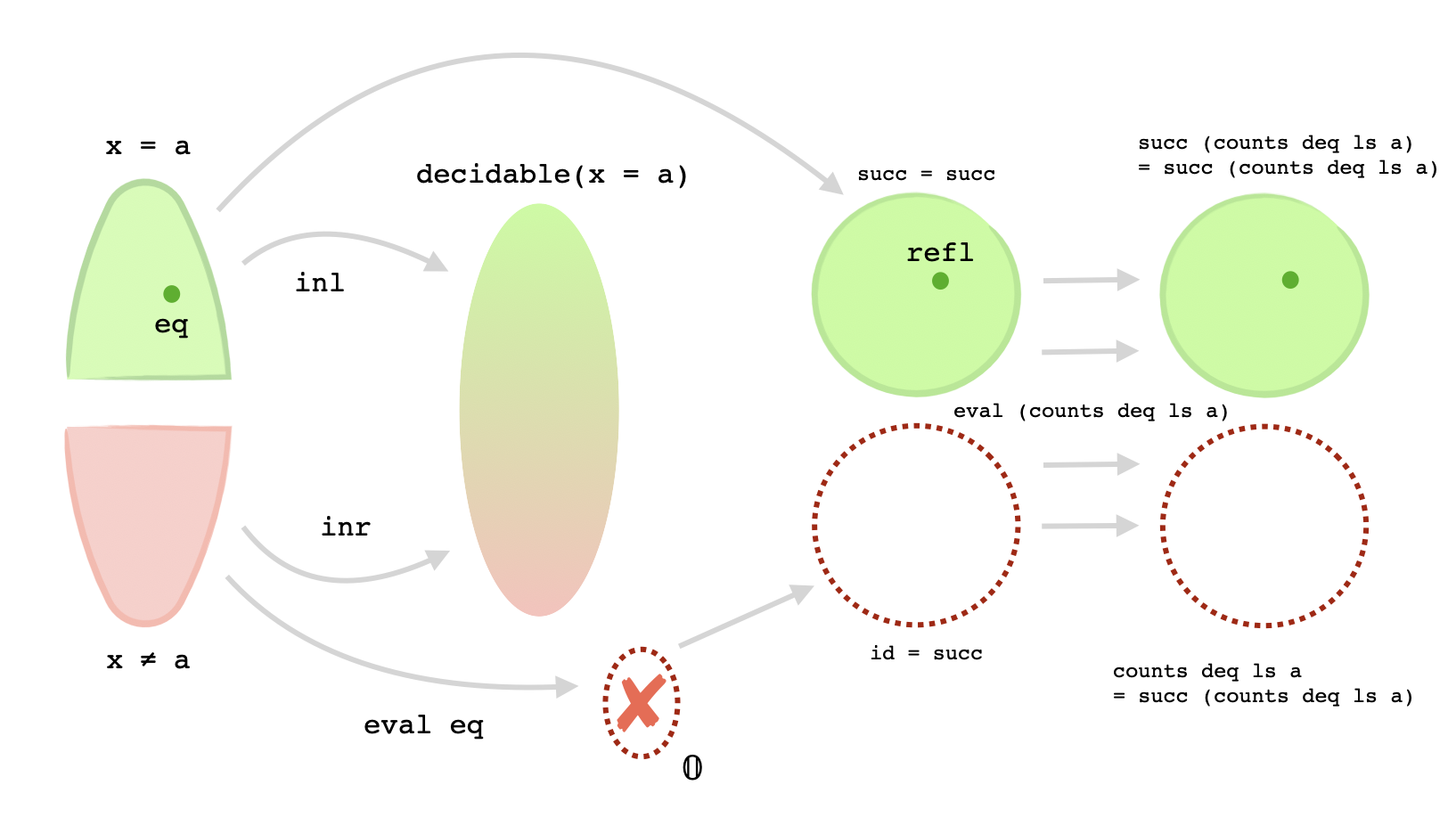
but it's not able to simplify the +-recursion expression call to either succ or id without knowing whether or not deq x a results in something that looks like inl equal or inr not-equal. And even though something of type $x \equiv a$ is passed to this function as an argument, Agda can't make the final leap of deducing from this that whatever is returned from deq x a will have to fall inside the left half of the coproduct $\mathtt{decidable}(x\equiv a)$, or the half containing proofs that $x\equiv a$. A little piece of insight is missing, namely the fact that receiving something from the right half of the coproduct, i.e. the half containing proofs that $x\not \equiv a$, would contradict the preexisting proof eq that $x\equiv a$. That's right - there's actually a small proof by contradiction hidden inside the proof of this innocuous claim!

Since Agda cannot infer what the output of (deq x a) will look like, we'll have to perform a case-split depending on whether its output looks like inl equal or inr not-equal. The second case, of course, will be an "absurd" case. This time, however, we can't use +-recursion to do our case split. This is because we will actually be defining a dependent function out of the sum type $(x\equiv a) + \neg (x\equiv a)$. That is, +-recursion will only help us when the output has the same type for inputs in the left half and the right half of the domain. But for the function we're writing, when (deq x a) evaluates to something that looks like inl equal, the +-recursion on the left hand side of the equality type defining the output can be reduced, giving the following output type:

succ (counts deq ls a) ≡ succ (counts deq ls a)

which is clearly inhabited by refl (succ (counts deq ls a)). On the other hand, if deq x a were to evaluate to something of the form inr not-equal, then the output type would simplify to

counts deq ls a ≡ succ (counts deq ls a)

which of course is not an inhabited type - but this is okay, because deq x a should never evaluate to a proof of inequality, since a proof of equality was passed as an argument. We don't actually need to procure an element of the above type - we just need to show that inr not-equal would produce a contradiction, i.e. an element of the empty type $\mathbb 0$, and then use an absurd pattern. Here's a picture visualizing our plan of attack:

Now we're finally ready to write the body of this function:

cons-eq-succ-count :
  {A : 𝓤 ̇}
  → (deq : has-decidable-equality A)
  → (ls : List A)
  → (a x : A)
  → (x ≡ a)
  → (counts deq (cons x ls) a) ≡ succ (counts deq ls a)
cons-eq-succ-count deq ls a x eq
  = ap (λ f → f (counts deq ls a))
    (+-induction
      (λ yneq → +-recursion (λ _ → succ) (λ _ → id) yneq ≡ succ)
      (λ eq' → refl succ)
      (λ neq → ex-nihilo (neq eq))
      (deq x a))

Notice that +-induction takes an additional argument (its first argument) used to explicitly specify the type family for its output. In the case in which deq x a evaluates to something of the form inl eq', Agda knows how to finish the job - hence the second argument λ eq' → refl succ. The second case, where we employ the absurd pattern, is the tricky one. If deq x a were to instead evaluate to something of the form inr neq, we could still obtain a proof of the desired type by first obtaining something of type $\mathbb 0$, which can be done by evaluating $\mathtt{neq}:(x\equiv a)\to\mathbb 0$ at the argument $\mathtt{eq}:x\equiv a$, and from there anything follows. Notice that this part of the case split doesn't really have any computational content, since it can never actually be evaluated. It's just a "formality" to convince the type checker that we're taking all possibilities into account.

We can write a similar proof for our second helper function, but for this one the first case will be the absurd one, since the assumption is that $x$ and $a$ are unequal:

cons-neq-same-count :
  {A : 𝓤 ̇}
  → (deq : has-decidable-equality A)
  → (ls : List A)
  → (a x : A)
  → ¬ (x ≡ a)
  → (counts deq (cons x ls) a) ≡ counts deq ls a
cons-neq-same-count deq ls a x neq
  = ap (λ f → f (counts deq ls a))
    (+-induction
      (λ yneq → +-recursion (λ _ → succ) (λ _ → id) yneq ≡ id)
      (λ eq → ex-nihilo (neq eq))
      (λ neq' → refl id)
      (deq x a))

Now we're ready to write our final proof! We've proven our proposition for the case in which the first list was empty, so now we need to consider the following case:

append-sum-counts deq (cons x ls1) ls2 a = _

Depending on whether $x$ and $a$ or equal or not, we will follow one of two different lines of reasoning - but our output type will be the same, namely the type

counts deq (append (cons x ls1) ls2) a ≡ (counts deq (cons x ls1) a) +̇ (counts deq ls2 a)

so it makes sense to use +-recursion rather than +-induction for this case split. So we'll want to write a definition that looks something like this:

append-sum-counts deq (cons x ls1) ls2 a = 
  = +-recursion
     (λ eq → _)
     (λ neq → _)
     (deq x a)

If it turns out that $x\equiv a$, then there are three intermediate equalities involved in arriving at the desired result. Firstly, we will have that counts deq (append (cons x ls1) ls2) a is equal to succ (counts deq (append ls1 ls2) a), the result of one of our previous lemmas. Secondly, we will have that this is equal to succ ((counts deq ls1 a) +̇ (counts deq ls2 a)), the result of a recursive call to the previous case of our function (in which the first argument has one element fewer). Thirdly, we will have that this is equal to (counts deq (append x ls1) a) +̇ (counts deq ls2 a), which also follows from our first lemma. Similarly, the case of $x\not\equiv a$ can be split into three intermediate equalities, with the difference being that there is no succ applied to both sides of the equality. Hence, we can arrive at the following final implementation:

append-sum-counts deq (cons x ls1) ls2 a
  = +-recursion
     (λ eq →
       (cons-eq-succ-count deq (append ls1 ls2) a x eq)
       ∙ (ap succ (append-sum-counts deq ls1 ls2 a))
       ∙ (ap (λ y → y +̇ (counts deq ls2 a)) (cons-eq-succ-count deq ls1 a x eq) ⁻¹))
     (λ neq →
       (cons-neq-same-count deq (append ls1 ls2) a x neq)
       ∙ (append-sum-counts deq ls1 ls2 a)
       ∙ (ap (λ y → y +̇ (counts deq ls2 a)) (cons-neq-same-count deq ls1 a x neq) ⁻¹))
     (deq x a)

And this type-checks, completing our proof of the proposition! It still baffles me how long it took me to understand how to deal with the case-split, and why it was even necessary at all to use +-induction at all.