Skip to page content Inicio     Entradas     CV     Contacto     Gente     RSS

Topología para la genética

En una entrada anterior he tratado una interpretación de la topología que me parece muy esclarecedor. En breve:

• Un elemento $x\in X$ de un espacio topológico representa una entidad cuya identidad tal vez no se puede saber con exactitud.
• Un entorno $N$ de un punto $x\in X$ del espacio topológico representa un conjunto que es tal que se puede confirmar que $x\in N$ a pesar de no conocer la identidad de $x$ con exactitud.
• Un conjunto abierto $U\subset X$ es un conjunto semidecidible, es decir, un conjunto que es entorno de todos sus puntos, o un conjunto que describe una propiedad que se puede confirmar para cada punto que la posea.
• El conjunto vacío $\varnothing$ es abierto porque no contiene ningún punto y el conjunto total $X$ es abierto porque contiene todos los puntos.
• Una unión de abiertos $U_i$ es abierto, porque al verificar que $x$ pertenezca a algún $U_i$ concreto, se habrá verificado que pertenece a la unión.
• Una intersección finita de abiertos es abierto, porque al verificar que $x$ pertenezca a cada uno de ellos a su vez, se habrá verificado que pertenece a su intersección.

Anteriormente consideré esta interpretación en términos computacionales - se ha tratado de propiedades que se puede computar sabiendo sólo la identidad de una entidad hasta precisión finita, por ejemplo en las representaciones aproximadas de números reales. Pero en esta entrada quiero ampliar esta punto de vista usando la topología para modelar no sólo propiedades computacionales sino también observaciones empíricas sobre sistemas naturales cuyo estado interno no se puede saber con certeza desde fuera. En concreto, veremos como se la puede usar para describir la genética, siendo el datos "oculto" la información genética de un organismo, a la que sólo se puede acceder de forma limitada a través de la manera en la que se manifiesta en las características físicas del organismo.

Fundamentos genéticos

Primero introducimos un poco de terminología de la genética. Los organismos que se reproducen sexualmente suelen recibir varios copias de sus genes de sus padres y en particular los organismos diploides poseen dos copias de cada cromosoma, siendo uno de cada padre. Si la sucesión de ADN que controla un gen concreto del organismo está localizado en una ubicación de un cromosoma, se dice que esta ubicación es el locus de este gen. Los distintos posibles secuencias de ADN que pueden ocupar ese locus y constituir ese gen se llaman los alelos del gen. Cuando un organismo se reproduce con otro, su cría recibe un cromosoma de cada padre y se suele suponer que el que se recibe de cada padre está seleccionado al azar.

Entonces, ¿qué sucede si un organismo diploide posee dos distintos alelos del mismo gen, uno en cada cromosoma? Pues lo que se observa con frecuencia es que uno de los alelos sea dominante y que otro sea recesivo, de tal manera que la manifestación de la característica física que codifica el gen está determinada por la presencia o la ausencia de la variante dominante. La combinación de alelos que posee un organismo se llama su genotipo mientras que la característica que presenta por causa de estos genes se llama su fenotipo.

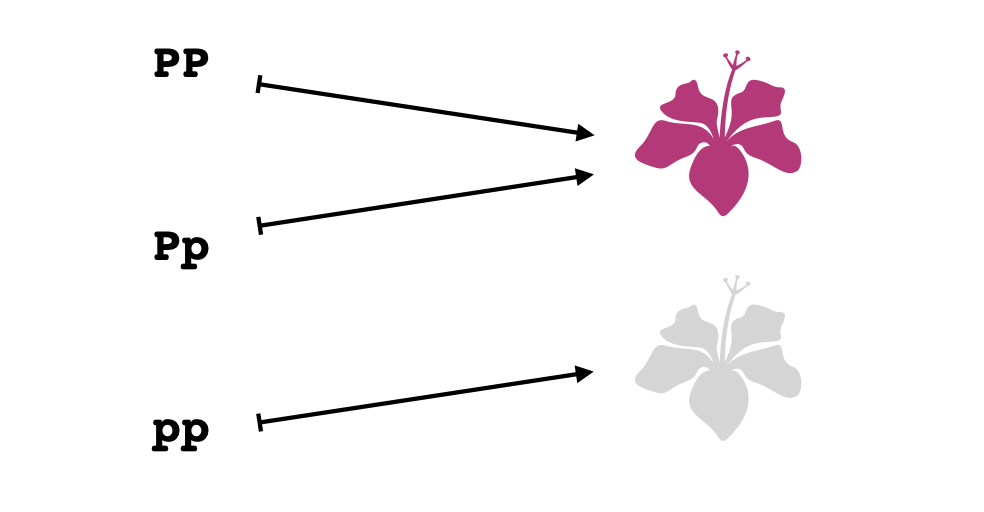
Por ejemplo, entre los genes de una planta floreciente, puede que en el gen que determina la producción de pigmentos morados en la flor tenga un posible alelo ($P$) que provoca la producción del pigmento y otro ($p$) que no. En este caso basta una única copia del alelo que produce el pigmento para que se manifieste el color morado en las flores. Así que, tanto las plantas del genotipo $PP$ como las del genotipo $Pp$ tendrán flores moradas mientras que sólo las plantas del genotipo $pp$ manifestarán flores blancas (sin pigmento). Los organismos con dos copias del mismo alelo se llaman homocigotos mientras que los que tienen distintos alelos se llaman heterocigotos.

Aporte topológico

El aspecto interesante de este mecanismo de herencia en cuanto a la topología y su capacidad de modelar el conocimiento parcial es que no se puede deducir directamente el genotipo de un organismo de su fenotipo. Por ejemplo, dada una planta con una flor blanca, se sabe que su genotipo es seguramente $pp$, pero dada una planta con una flor blanca, no se sabe (a lo menos de inmediato) si su genotipo es $PP$ o $Pp$.

Pero aunque los genotipos $PP$ y $Pp$ le corresponden al mismo fenotipo no cabría decir que sean indistinguibles un organismo con genotipo $PP$ y uno con genotipo $Pp$. Por ejemplo, al reproducir con otra planta de flores blancas, producirán descendientes con distribuciones de colores distintas. Un cruce $PP\times pp$ sólo puede producir descendientes del genotipo $Pp$ y con flores moradas, pero un cruce $Pp\times pp$ puede producir tanto descendientes del genotipo $Pp$ (flores moradas) como descendientes del genotipo $pp$ (flores blancas).

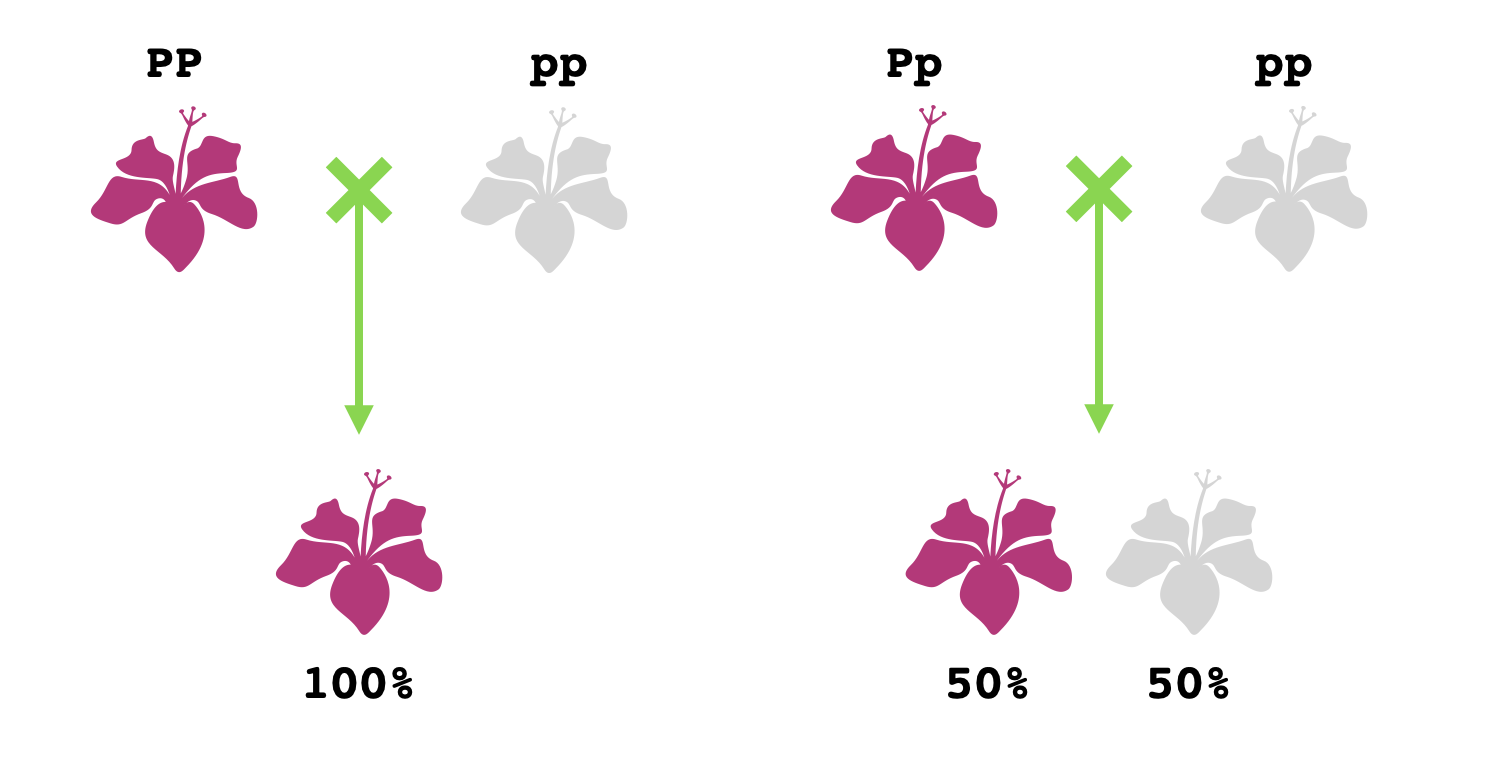
Por tanto, si se tiene una planta con flores moradas y de genotipo desconocido, se la cruza con una planta con flores blancas, y se obtiene así una planta con flores blancas, la primera planta tendría que tener el genotipo $Pp$. Pero fíjate que si esa planta original con flores moradas en la realidad tiene genotipo $PP$, no hay procedimiento que permite concluir con certeza que es homocigoto. Una planta $PP$ se comporta de manera indistinguible de una planta $Pp$ que, por muy improbable que sea, siempre pasa el alelo $P$ a sus descendientes. La cuestión de distinguir entre una planta $PP$ y una $Pp$ es entonces más liada que determinar si son "distinguibles" o "indistinguibles" - es que una $Pp$ se puede distinguir de un $PP$ pero una $PP$ no se puede distinguir de un $Pp$.

El esquema conceptual que utiliza la topología para expresar "conjuntos semidecidibles" como conjuntos abiertos nos permite describir este fenómeno en formato breve. El problema de extraer información sobre el genotipo de un organismo se puede representar como un espacio topológico con tres elementos: los tres genotipos $PP$, $Pp$ y $pp$. Acabamos de comentar que si se tiene una planta con genotipo $pp$ se lo sabrá de inmediato por el color de sus flores, así que ${pp}$ debe ser un conjunto abierto. Además, dado una planta con genotipo $PP$ o $Pp$ se sabrá de inmediato que tiene uno de estos dos genotipos por el color de sus flores, y por tanto ${PP, Pp}$ debe ser conjunto abierto. Finalmente, si se tiene una planta heterocigota $Pp$ se puede confirmar su genotipo observando que produce descendientes con flores blancas, así que ${Pp}$ debe ser un abierto. Lo que resulta es la siguiente topología en el conjunto ${PP, Pp, pp}$:

Fíjate que una topología en el conjunto de genotipos nos da una manera concisa y exhaustiva de expresar qué tipo de conocimiento podemos poseer en cada circunstancia posible. A continuación veremos unos ejemplos teóricos de particularidades que pueden complicar la herencia y cómo influyen en la topología que usamos para expresar el conocimiento verificable que se puede obtener.

Dominancia incompleta

Dominancia incompleta es un fenómeno en el que se puede observar una diferencia entre los fenotipos de un homocigoto dominante y un heterocigoto para alguna característica. Por ejemplo, en el caso del color de las flores, si dos copias del alelo dominante $P$ resultan en una producción de pigmento que supera por mucho la producción de pigmento que se logra con una sola copia, entonces puede que los heterocigotos presenten un color más tenue, así:

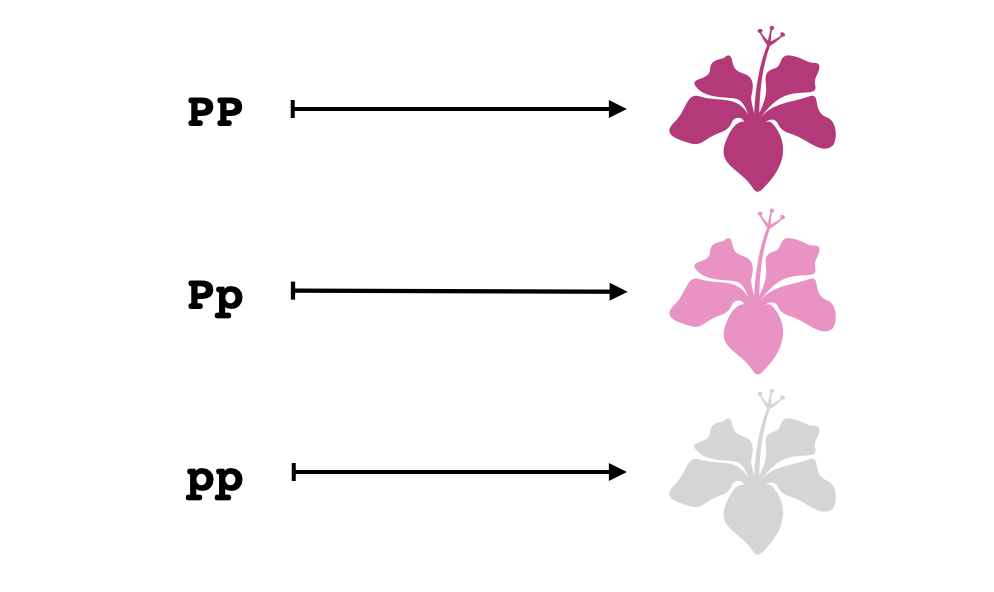
Si fuera así esta característica entonces podríamos distinguir fácilmente entre todos los posibles genotipos simplemente observando el fenotipo, pues a cada fenotipo le correspondería un único genotipo. Por tanto la topología que corresponde a este locus sería la topología discreta en tres puntos:

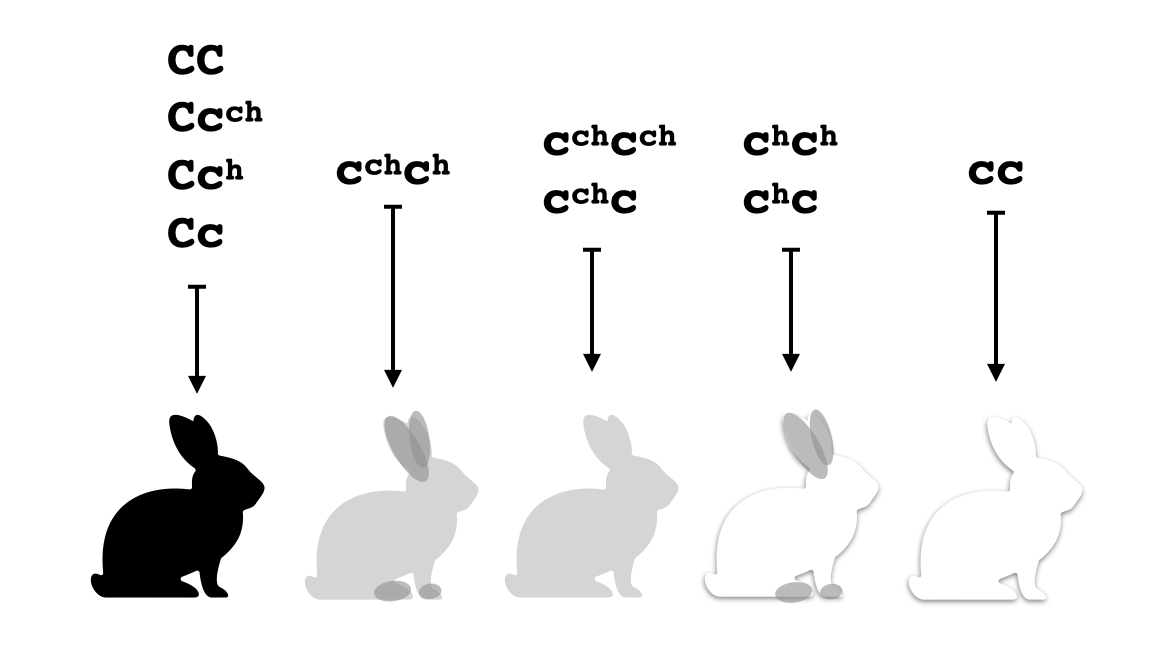
En este caso la dominancia incompleta trivializa el problema, pero hay casos más complicados en los que produce comportamiento interesante. Por ejemplo, hay un gene que controla el color del pelaje en los conejos con cuatro alelos distintos $C,c^\mathtt{ch}, c^\mathtt{h}, c$ que tienen el siguiente comportamiento:

• $C$ produce una enzima que fabrica pigmento normalmente, la cual resulta en pelo negro por todo el cuerpo.
• $c^\mathtt{ch}$ produce una enzima menos eficaz que produce pigmento en una menor cantidad, la cual resulta en pelo gris (a menos que haya otra enzima que produce pigmento en mayor cantidad).
• $c^\mathtt{h}$ produce una enzima muy sensible a la temperatura que no funciona en absoluto en altas temperaturas. Por tanto, sólo produce pigmento en las extremidades del conejo (las patas y las orejas) y en esos sitios lo produce normalmente.
• $c$ produce una enzima que no funciona para nada.

Fíjate que en la presencia del alelo $C$ no se puede observar directamente la presencia de ninguno de los otros alelos, pues se producirá pigmento negro en grandes cantidades por todo el pelaje del conejo. Por eso se dice que $C$ es completamente dominante a los otros tres alelos. Por otro lado, $c^\mathtt{ch}$ es incompletamente dominante a $c^\mathtt{h}$, como en el genotipo heterocigoto con estos dos alelos, se puede observar una mezcla de las dos características - pelaje negro en las extremidades y pelaje gris por el resto del cuerpo. He tenido un poco de dificultad en encontrar buenas fuentes en el internet que describen sin ambigüedad las relaciones de dominancia entre los cuatro alelos de este gen, pero a partir de ahora vamos a suponer que resultan en los $5$ fenotipos siguientes, que es lo que he entendido yo según lo que he leído:

Si es así, entonces la topología que se podría usar para describir lo que se puede deducir sobre el genotipo de un conejo con certeza es la siguiente:

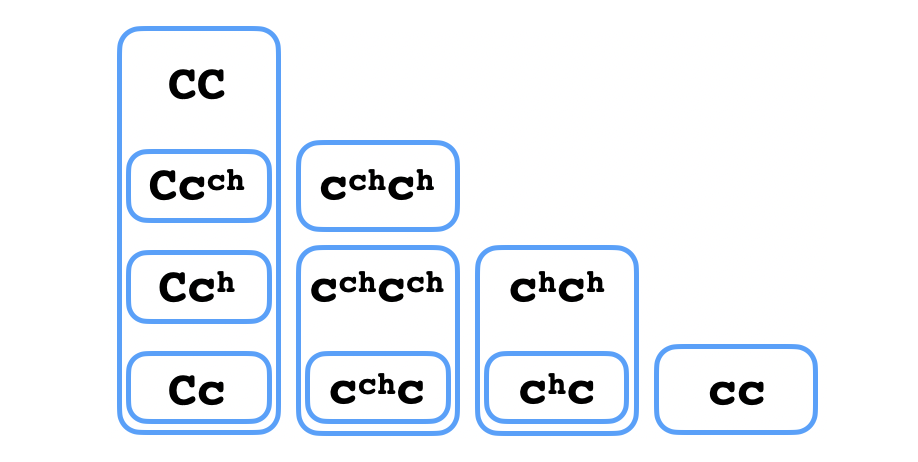
¿Ves por qué? Para cada abierto de este diagrama y cada elemento de éste ¿puedes describir una observación que confirmaría la pertenencia del genotipo de un organismo a ese abierto?

Epistasia

Se puede considerar también multiples características de un organismo a la vez que son codificadas por distintos genes. Por ejemplo, si un gen con alelos $A,a$ controla el color del pelo de una persona y un gen con alelos $B,b$ controla el color de sus ojos, pues como ya sabemos las topologías en los conjuntos ${AA,Aa,aa}$ y ${BB,Bb,bb}$ que obtenemos considerando estas características por separados, podemos obtener la topología en el conjunto $$\begin{Bmatrix} AABB & AaBB & aaBB \\ AABb & AaBb & aaBb \\ AAbb & Aabb & aabb \end{Bmatrix}$$ que describe la consideración simultánea de las dos características a la vez, tomando la topología producto en este conjunto. En este caso la topología es:

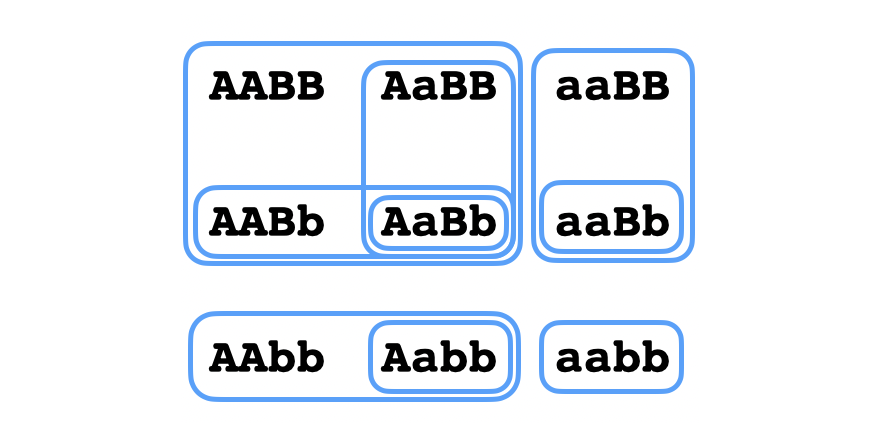
El término epistasia se refiere a una interacciones entre genes en el que el genotipo con respecto a uno de los genes influye en la expresión de un fenotipo codificado por otro gen, a diferencia del ejemplo anterior en el que las dos características son independientes. Por ejemplo, suponemos esta vez que un gen con alelos $A,a$ controla el color del pelo mientras que un gen con alelos $B,b$ controla si una persona es calvo o no (suponiendo que ser calvo es dominante). En este caso se tiene que la segunda característica puede ocultar el fenotipo con respecto a la primera característica - si una persona es calvo, da igual el color que tendría su pelo si lo tuviera porque no se lo puede observar. En este caso el mapeo de genotipo a fenotipo es el siguiente:

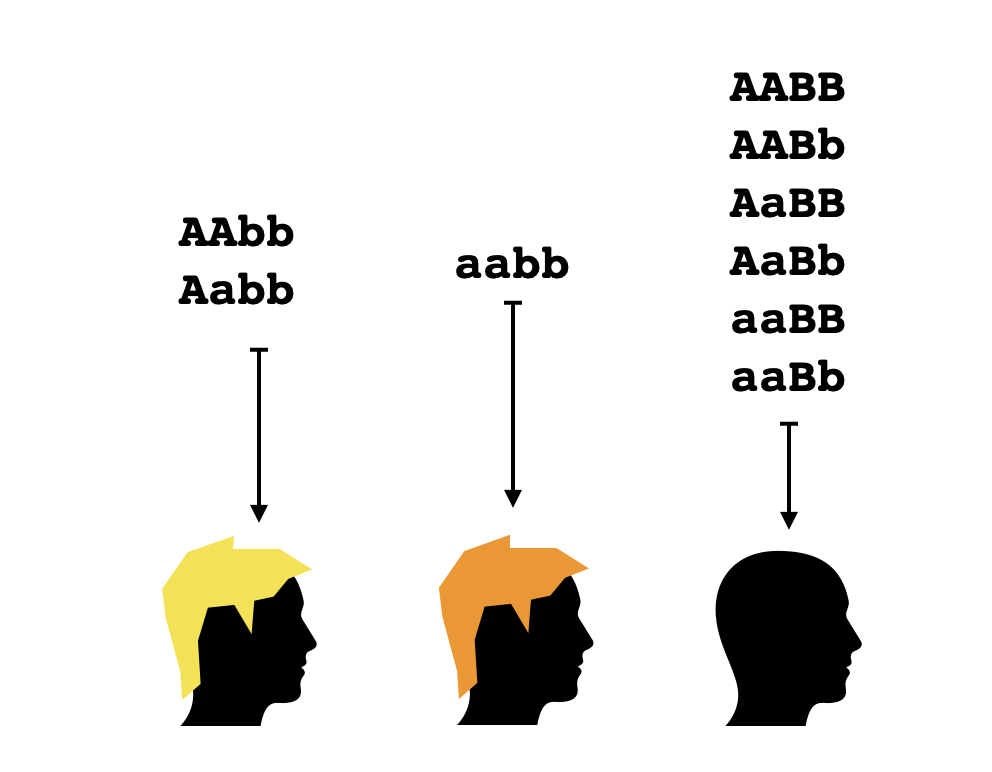
En una topología finita como las que vamos considerando, se puede considerar el abierto básico $B_g$ sobre cada punto $g$, o sea el abierto más pequeño que contenga ese punto, o la intersección de todos los abiertos que lo contienen. Para un genotipo $g$, el básico $B_g$ representa el conocimiento más específico que se puede llegar a tener sobre un organismo de ese genotipo. Es un buen rompecabezas determinar cuáles exactamente son los conjuntos abiertos (básicos) en la topología que corresponde a esta combinación de características. La topología que he calculado yo es la siguiente:

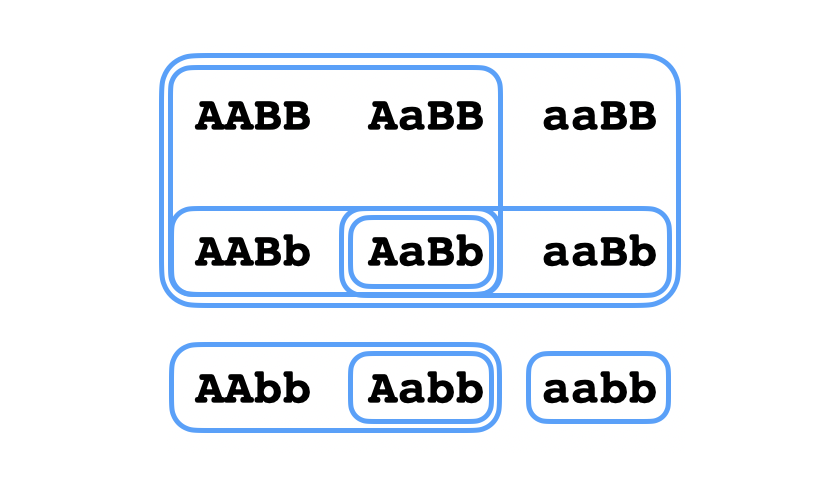
El caso más interesante para considerar era $aaBB$, es decir el genotipo cuyo abierto básico es el más grande, o sea el genotipo de una persona sobre la que se puede deducir lo más mínimo. Podemos describir los $9$ abiertos básicos $B_g$ de esta topología en términos de las observaciones sobre una persona de genotipo $g$ que nos llevamos a concluir la pertenencia de su genotipo a $B_g$:

1. $B_\mathtt{aabb}$ incluye personas con pelo castaño.
2. $B_\mathtt{AAbb}$ incluye personas con pelo rubio.
3. $B_\mathtt{Aabb}$ incluye personas con pelo rubio que pueden tener hijos de pelo castaño al reproducir con alguien de pelo castaño.
4. $B_\mathtt{aaBb}$ incluye personas calvas que pueden tener hijos de pelo castaño al reproducir con alguien de pelo castaño.
5. $B_\mathtt{AABb}$ incluye personas calvas que pueden tener hijos de pelo rubio al reproducir con alguien de pelo castaño.
6. $B_\mathtt{AaBb}$ incluye personas calvas que pueden tener tanto hijos de pelo castaño como hijos de pelo rubio al reproducir con alguien de pelo castaño.
7. $B_\mathtt{AABB} = B_\mathtt{AaBB}$ incluye personas calvas que pueden tener hijos que pertenecen a $B_\mathtt{AaBb}$.
8. $B_\mathtt{aaBB}$ incluye todas personas calvas. Es decir, $aaBB$ no se puede distinguir de ningún otro genotipo de una persona calva (aunque éstos a veces de pueden distinguir entre sí).

Para abordar una posible confusión: tal vez de parece que el conjunto ${aaBB, aaBb, AaBB, AaBb}$ debe ser también abierto, como estos son los únicos genotipos que se pueden cruzar con $AAbb$ para obtener un hijo con uno de los genotipos de $B_\mathtt{aaBb} = {aaBb, AaBb}$, y como esto es otro abierto se podrá verificar cuando su hijo tiene un genotipo de $B_\mathtt{aaBb}$. Pero esto no es un experimento válido porque para estar seguro del resultado habrá que estar seguro de haber cruzado definitivamente con una persona del genotipo $AAbb$. Pero este genotipo no es verificable. No se podrá observar que la persona con la que se está reproduciendo tiene genotipo $AAbb$, sino sólo que pertenece a $B_\mathtt{AAbb} = {AAbb, Aabb}$, y si se cruza cualquiera persona calva con una persona de un genotipo que puede ser o $AAbb$ o $Aabb$ el resultado puede ser un hijo de $B_\mathtt{aaBb}$. Es por eso que $B_\mathtt{aaBB}$ no es ${aaBB, aaBb, AaBB, AaBb}$ sino el conjunto de todos los genotipos que corresponden a ser calvo.

Ejercicios

Aquí están algunos casos adicionales para considerar. Son puramente teóricos y no sé si tienen base en la genética real.

1. Imagínate que hay tres alelos $A_0,A_1,A_2$ de un gen que codifican tres fenotipos distintos y que son tales que que $A_0$ es totalmente dominante sobre $A_1$, $A_1$ es totalmente dominante sobre $A_2$ y $A_2$ es totalmente dominante sobre $A_0$. ¿Puedes dibujar la topología en los $6$ genotipos posibles que describe lo que se puede deducir sobre el genotipo de un organismo?
2. Considera el caso de las flores que tratamos al principio de la entrada, pero esta vez supón que hay una enfermedad (que no se hereda y que se contagia al azar) que causa que una planta tenga flores azules no obstante de su genotipo. Cada planta puede tener cualquier uno de los tres genotipos $PP, Pp, pp$ pero también puede o tener la enfermedad o no tenerla, así que hay $6$ estados posibles y sólo dos posibles colores. Encuentra la topología correspondiente. ¿Qué tal si la enfermedad produce siempre flores moradas? ¿Flores blancas?
3. Considera de nuevo el ejemplo de los genes del color de pelo y de ser calvo. ¿Cuál sería la topología si ser calvo es recesivo en vez de dominante?

The posts on this website are licensed under CC-by-NC 4.0.