Skip to page content Home     Posts     CV     Contact     People

Fractional iterates

2017 Dec 8

In previous posts, I've written about finding formulas for $f^{\circ n}$ in terms of $n$, but I've considered iterates of $f$ only for integer values of $n$. I will now discuss an extension of the definition of $f^{\circ n}$ to include rational non-integer values of $n$.

Find half-iterates of the functions $$a(x)=x^2+2x$$ $$b(x)=x+(-1)^{\lfloor x\rfloor}$$ and find a continuous half-iterate of the function $$c(x)=e^x$$

Recall that function iteration has the properties $$f^{\circ n}\circ f=f\circ f^{\circ n}=f^{\circ n+1}$$ and $$(f^{\circ n})^{\circ m}=f^{\circ mn}$$ The second property might lead us to say that $$(f^{\circ 1/n})^{\circ n}=f$$ and so we shall define $f^{\circ 1/n}$ as any function satisfying $$(f^{\circ 1/n})^{\circ n}=f$$ Notice that I say any function, as such functions are not always unique. For example, consider $\text{id}{\mathbb R}^{\circ 1/2}$. The functions $\text{id}{\mathbb R}$ and $-\text{id}{\mathbb R}$ iterated twice both yield $\text{id}{\mathbb R}$, providing an example of how half-iterates are not always unique. Thus we may think of the fractional iterate $f^{\circ 1/n}$ not as a function, but as as set of functions, each of which, when iterated $n$ times, yield the function $f$. Using our previous example, we might say that $$\text{id}_{\mathbb R}\in \text{id}_{\mathbb R}^{\circ 1/2}$$ and $$-\text{id}_{\mathbb R}\in \text{id}_{\mathbb R}^{\circ 1/2}$$

First I will tackle the problem of finding all continuous functions in the set $\text{id}{\mathbb R}^{\circ 1/2}$ - or the set of continuous involutions on the reals. Notice that I say continuous - in this post, I will not deal with any non-continuous function, since they can get pretty messy. We've already noted that $-\text{id}{\mathbb R}$ is in this set. With a bit of further analysis, one may observe that all functions in the form $$g^{-1}(-g(x))$$ satisfy it as well, if $g:\mathbb R\mapsto\mathbb R$.

But is this set of solutions exhaustive? That is, if $f:\mathbb R\mapsto\mathbb R$ satisfies $f^{\circ 2}=\text{id}_{\mathbb R}$, does there necessarily exist a function $g:\mathbb R\mapsto\mathbb R$ such that $f(x)=g^{-1}(-g(x))$?

The answer is yes, but proving it will take a little bit of work. First we must prove a property that all half-iterates of the identity function share.

Notice first that if a function $f$ is non-injective, then the function $f^{\circ 2}$ is also non-injective. Thus, if $f$ is a half-iterate of the identity function, since the identity function is injective, $f$ must also be injective. Continuous and injective functions are always either increasing or decreasing, implying that $f$ is either increasing or decreasing. So for now, suppose that $f$ is increasing.

Suppose that $f(x)\gt x$ for some $x$. Then, since $f$ is increasing, $f^{\circ 2}(x)\gt f(x)$ and, since $f^{\circ 2}=\text{id}{\mathbb R}$, we have $x\lt f(x)$. Contradiction! If we instead suppose that $f(x)\lt x$ for some $x$, we arrive at a similar contradiction. Thus we have that if $f$ is increasing, than $f$ cannot be greater than or less than its input for any input, meaning that $f=\text{id}{\mathbb R}$. Thus, the only continuous increasing function in $\text{id}_{\mathbb R}^{\circ 1/2}$ is the identity function.

This tells us that the only continuous increasing involution on the reals is the identity function, meaning that all others must be decreasing. This is the property that I wanted to prove from the beginning. Since all such functions are decreasing, they must all have exactly one fixed point. If $f^{\circ 2}=\text{id}{\mathbb R}$ and $f$ is continuous and decreasing, I will call its fixed point $\phi$. Let us now define $$g(x)= $$\begin{cases} h(x), &\text{if $x\ge \phi$}\\ -(h\circ f)(x), &\text{if $x\lt \phi$} \end{cases}$$ $$ for any continuous, injective function $h$ with $h(\phi)=0$. From here, it is trivial to verify that both $g$ is continuous and that $g^{-1}(-g(x))=f(x)$, showing that for any function $f$ in $\text{id}{\mathbb R}^{\circ 1/2}$, there exists a continuous function $g$ such that $g^{-1}(-g(x))=f(x)$, thus showing that the set of functions in the form $g^{-1}(-g(x))$ for continuous and injective $g$ provides an exhaustive set of continuous involutions on the real numbers.

Next I will consider continuous $\text{id}{\mathbb R}^{\circ 1/3}$ - which, thankfully, is a much easier problem. Again, the key is to notice that any continuous function $f\in\text{id}{\mathbb R}^{\circ 1/3}$ must be injective, and thus either increasing or decreasing. If $f$ is increasing, then we may use an argument similar to the one used previously to show that $f=\text{id}{\mathbb R}$. If $f$ is decreasing, then for all $x,y\in\mathbb R$, $$x\lt y\implies f(x)\gt f(y)$$ and so $$x\lt y\implies f^{\circ 2}(x)\lt f^{\circ 2}(y)$$ and $$x\lt y\implies f^{\circ 3}(x)\gt f^{\circ 3}(y)$$ making $f^{\circ 3}$ decreasing, which contradicts the fact that $f^{\circ 3}=\text{id}{\mathbb R}$. Thus the only continuous function in $\text{id}_{\mathbb R}^{\circ 1/3}$ is the identity function.

One can use decreasingness to prove the nonexistence of continuous half-iterates of many other functions, even if they aren't strictly decreasing. For example, suppose a differentiable function $f$ has a fixed point at $x=\phi$ such that $f'(\phi)$ is less than zero. Then, for some neighborhood $N$ of $\phi$, $f$ must be decreasing, since its derivative at $x=\phi$ is negative. If we now assume that a continuous $h\in f^{\circ 1/2}$ exists, we may state immediately that it is injective in $N$, since $f$ is injective in $N$. Thus it is either increasing or decreasing in $N$. But h being increasing or decreasing in $N$ both imply that $h^{\circ 2}=f$ is increasing in $N$, leading to a contradiction. This method can be used, for example, to show that the cosine function has no continuous half-iterate, since it is decreasing at its fixed point.

So far, all I've done is disprove the existence of half-iterates of functions. Now I will demonstrate how one might construct a specific half-iterate of a function.

Some functions have nice and neat closed-form half-iterates. For example, consider the function $$a(x)=x^2+2x$$ Because we can rewrite this as $$a(x)=(x+1)^2-1$$ we can easily find the following half-iterate $h\in a^{\circ 1/2}$: $$h(x)=|x+1|^{\sqrt 2}-1$$

Some functions have half-iterates that are a bit harder to find. Consider for example the function $$b(x)=x+(-1)^{\lfloor x\rfloor}$$ Some half-iterates of this function can be defined as piecewise functions. An example is $h_1,h_2\in b^{\circ 1/2}$: $$h_1(x)=\begin{cases}x+2&\text{if }\lfloor x\rfloor\equiv 0\pmod 4\\ x+2&\text{if }\lfloor x\rfloor\equiv 1\pmod 4\\ x-1&\text{if }\lfloor x\rfloor\equiv 2\pmod 4\\ x-3&\text{if }\lfloor x\rfloor\equiv 3\pmod 4 \end{cases}$$

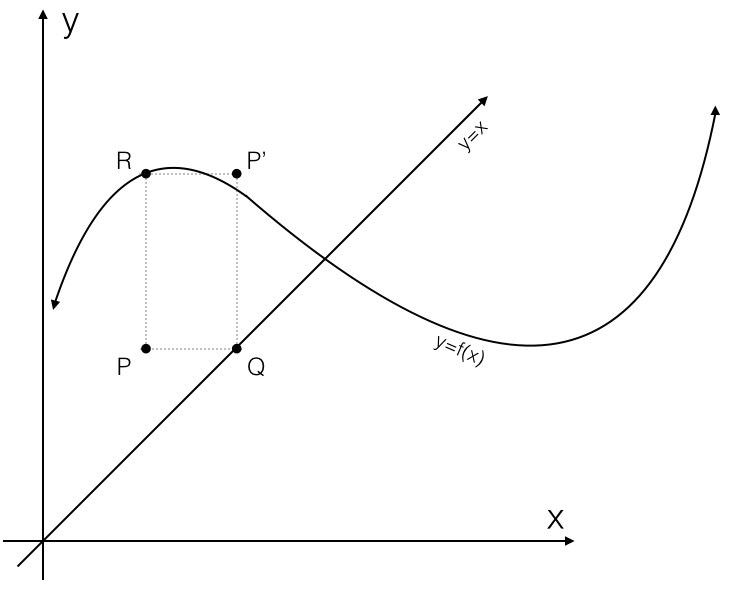
Sometimes, piecewise construction of half-iterates can get a little bit wild. Before I demonstrate a construction of a half-iterate of the exponential function, I must explain the graphical construction technique that I used for it. Imagine that $f:\mathbb R\mapsto\mathbb R$ is a function with half-iterate $h:\mathbb R\mapsto\mathbb R$, and suppose we know the value of $h(x_0)$ for some $x_0$. Let $h_0$ be this value. Then we have that $$h(x_0)=h_0$$ which implies $$h(h(x_0))=h(h_0)$$ or $$h(h_0)=f(x_0)$$ and we know another value of $h$! But we can take this even further and say that $$h(f(x_0))=f(h_0)$$ and so on. Let's think of this information in terms of the graph of $y=h(x)$. We were given initially that the point $(x_0,h_0)$ was on the graph, and from this, we determined that the points $(h_0,f(x_0))$ and $(f(x_0),f(h_0))$ were also on the graph. In general, if the point $(a,b)$ is on the graph of $y=h(x)$, then the point $(b,f(a))$ is also on the graph. Visually, this means that if we assume some point $P$ is on the graph of $y=h(x)$, we may use the following steps to find another point $P'$ on the graph:

• Plot the point $P$ and graph the curves $y=f(x)$ and $y=x$.
• Draw the horizontal line segment $PQ$, where $Q$ is on the graph of $y=x$.
• Draw the vertical line seqment $PR$, where $R$ is on the graph of $y=f(x)$.
• Construct rectangle $PQP'R$. Then the point $P'$ is also on the graph of $y=h(x)$.

Here is a picture illustrating this process:

Though it may sound complicated, this process is as easy as drawing a rectangle, and it can lead to some interesting results. For example, consider the function $f$ in my example graph (it does not matter exactly what function it is). By assuming that the point $P$ was on the graph of $y=h(x)$, we found the point $P'$ also on $y=h(x)$. Notice that $P$ lies below the curve $y=f(x)$ and $P'$ lies above it. Thus, if we assume $h$ to be continuous, then by the intermediate value theorem, the curves $y=f(x)$ and $y=h(x)$ must intersect at some $x$-value between the x-values of $P$ and $P'$. Thus, for some $x'$ in that interval, $$f(x')=h(x')$$ or $$h(h(x'))=h(x')$$ implying that $h$ has a fixed point at $x=h(x')$, and thus that $f$ also has this fixed point. But since $f$ only has one fixed point between the y-values of $P$ and $P'$ (call it $\phi$), then $$h(x')=\phi$$ This could go on - for example, we could keep drawing rectangles to find $P''$, and $P'''$, et cetera.

This method can be used to prove the following interesting result:

If a function $f:\mathbb R\mapsto\mathbb R$ has no fixed points and has a continuous half-iterate $h:\mathbb R\mapsto\mathbb R$, then $h(x)$ is between $x$ and $f(x)$ for all $x\in\mathbb R$.

This is a rather nice result, but the proof is unpleasant and uses a lot of casework, so I will omit it.

Now I will lay out my construction of a half-exponential function, as written in one of my answers on MSE:

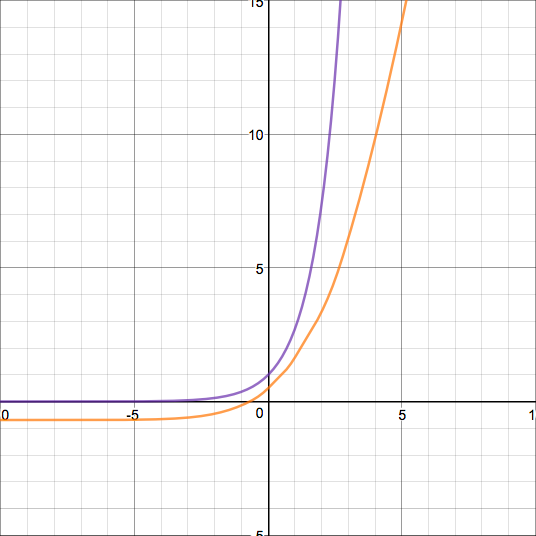
Define a sequence $a_n$ as follows: $$a_{-1}=-\log(2),\space\space a_0=0$$ $$a_{n+2}=\exp(a_n)$$ and define a sequence of functions $H_n$ as follows: $$H_{-2}(x)=\log(e^x+0.5)$$ $$H_{n+1}(x)=\exp(H^{-1}_n(x))$$ Then one may verify rather simply that the function $$h(x)=\begin{cases} H_{-2}(x) & \text{if} -\infty \lt x\le -\ln(2)\\ H_{n}(x) & \text{if} a_n \lt x\le a_{n+1} \end{cases}$$ or $$h(x)=\begin{cases} \ln(e^x+1/2) & \text{if} -\infty \lt x\le -\ln(2)\\ e^x-1/2 & \text{if} -ln(2) \lt x\le 0\\ x+1/2 & \text{if} 0 \lt x\le 1/2\\ e^{x-1/2}& \text{if} 1/2 \lt x\le 1\\ \text{etc...} \end{cases}$$ is a half-iterate of $e^x$. Amazingly, it can be proven by induction that this function is continuous and differentiable everywhere. Unfortunately, it is not twice-differentiable. Here is a graph of this function (in orange) alongside a graph of $y=e^x$ (in purple):

One might wonder if there exists a half-iterate of $e^x$ that is infinitely differentiable as $e^x$ is... but that topic will have to be left for a later blog post.